9.0: Prelude to Trigonometric Identities and Equations
- Page ID
- 1522
Math is everywhere, even in places we might not immediately recognize. For example, mathematical relationships describe the transmission of images, light, and sound. The sinusoidal graph in Figure \(\PageIndex{1}\) models music playing on a phone, radio, or computer. Such graphs are described using trigonometric equations and functions. In this chapter, we discuss how to manipulate trigonometric equations algebraically by applying various formulas and trigonometric identities. We will also investigate some of the ways that trigonometric equations are used to model real-life phenomena.
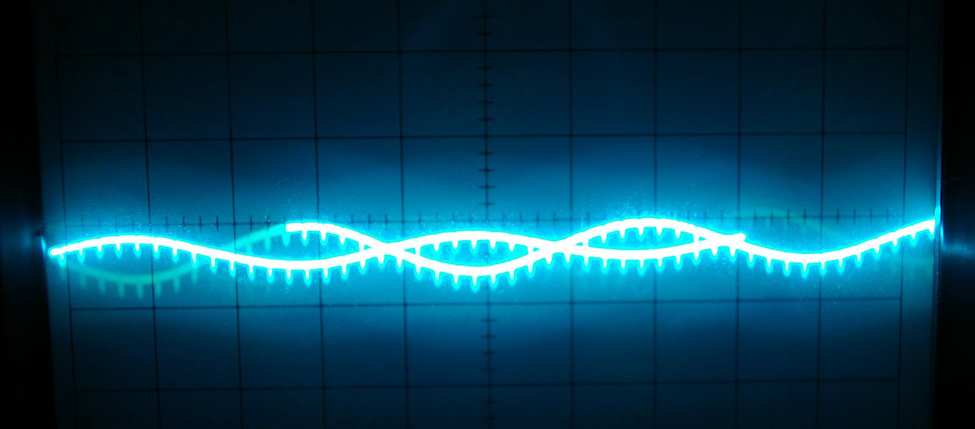
Figure \(\PageIndex{1}\): A sine wave models disturbance. (credit: modification of work by Mikael Altemark, Flickr).


