2.2: Operations on complex numbers
- Page ID
- 267
Even though we have formally defined \(\mathbb{C}\) as the set of all ordered pairs of real numbers, we can nonetheless extend the usual arithmetic operations on \(\mathbb{R}\) so that they also make sense on \(\mathbb{C}\). We discuss such extensions in this section, along with several other important operations on complex numbers.
2.2.1 Addition and subtraction of complex numbers
Addition of complex numbers is performed component-wise, meaning that the real and imaginary parts are simply combined.
Definition 2.2.1. Given two complex numbers \((x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{C}\), we define their complex sum to be
\[ (x_{1}, y_{1}) + (x_{2}, y_{2}) = (x_{1} + x_{2}, y_{1} + y_{2}). \]
Example 2.2.2. \( (3, 2) + (17, -4.5) = (3 + 17, 2 - 4.5) = (20, -2.5).\)
As with the real numbers, subtraction is defined as addition with the so-called additive inverse, where the additive inverse of \(z=(x,y)\) is defined a \(-z=(-x,-y)\).
Example 2.2.3. \( (\pi, \sqrt{2}) - (\pi/2, \sqrt{19}) = (\pi, \sqrt{2}) + (-\pi/2, -\sqrt{19}), \)
where
\[ (\pi, \sqrt{2}) + (-\pi/2, -\sqrt{19}) = (\pi - \pi/2, \sqrt{2} - \sqrt{19}) = (\pi/2, \sqrt{2} - \sqrt{19}). \]
The addition of complex numbers shares many of the same properties as the addition of real numbers, including associativity, commutativity, the existence and uniqueness of an additive identity, and the existence and uniqueness of additive inverses. We summarize these properties in the following theorem, which you should prove for your own
practice.
Theorem 2.2.4. Let \(z_{1}, z_{2}, z_{3} \in \mathbb{C}\) be any three complex numbers. Then the following statements are true.
- (Associativity) \((z_{1} + z_{2}) + z_{3} = z_{1} + (z_{2} + z_{3})\).
- (Commutativity) \(z_{1} + z_{2} = z_{2} + z_{1}\).
- (Additive Identity) There is a unique complex number, denoted \(0\), such that, given any complex number \(z \in \mathbb{C}\), \(0 + z = z\). Moreover, \(0 = (0, 0)\).
- (Additive Inverses) Given any complex number \(z \in \mathbb{C}\), there is a unique complex number, denoted \(-z\), such that \(z + (-z) = 0\). Moreover, if \(z = (x, y)\) with \(x, y \in \mathbb{R}\), then \(-z = (-x, -y)\).
The proof of this theorem is straightforward and relies solely on the definition of complex addition along with the familiar properties of addition for real numbers. For example, to check commutativity, let \(z_{1} = (x_{1}, y_{1})\) and \(z_{2} = (x_{2}, y_{2})\) be complex numbers with \(x_{1}, x_{2}, y_{1}, y_{2} \in \mathbb{R}\).
Then
\[
z_{1} + z_{2} =
(x_{1} + x_{2}, y_{1} + y_{2}) =
(x_{2} + x_{1}, y_{2} + y_{1}) =
z_{2} + z_{1}.
\]
2.2.2 Multiplication and division of complex numbers
The definition of multiplication for two complex numbers is at first glance somewhat less straightforward than that of addition.
Definition 2.2.5. Given two complex numbers \((x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{C}\), we define their complex product to be
\[ (x_{1}, y_{1})(x_{2}, y_{2}) = (x_{1}x_{2} - y_{1}y_{2} , x_{1}y_{2} + x_{2}y_{1}). \]
According to this definition, \(i^2=-1\). In other words, \(i\) is a solution of the polynomial equation \(z^2+1=0\), which does not have solutions in \(\mathbb{R}\). Solving such otherwise unsolvable equations was largely the main motivation behind the introduction of complex numbers. Note that the relation \(i^2=-1\) and the assumption that complex numbers can be multiplied like real numbers is sufficient to arrive at the general rule for multiplication of complex numbers:
\begin{align*}
(x_{1} + y_{1}i)(x_{2} + y_{2}i)
& =
x_{1}x_{2} + x_{1}y_{2}i + x_{2}y_{1}i + y_{1}y_{2}i^{2}
\\
& =
x_{1}x_{2} + x_{1}y_{2}i + x_{2}y_{1}i - y_{1}y_{2}
\\
& =
x_{1}x_{2} - y_{1}y_{2} + (x_{1}y_{2} + x_{2}y_{1})i.
\end{align*}
As with addition, the basic properties of complex multiplication are easy enough to prove using the definition. We summarize these properties in the following theorem, which you should also prove for your own practice.
Theorem 2.2.6. Let \(z_{1}, z_{2}, z_{3} \in \mathbb{C}\) be any three complex numbers. Then the following statements are true.
- (Associativity) \((z_{1}z_{2})z_{3} = z_{1}(z_{2}z_{3})\).
- (Commutativity) \(z_{1}z_{2} = z_{2}z_{1}\).
- (Multiplicative Identity) There is a unique complex number, denoted \(1\), such that, given any \(z \in \mathbb{C}\), \(1 z = z\). Moreover, \(1 = (1, 0)\).
- (Distributivity of Multiplication over Addition) \(z_{1}(z_{2} + z_{3}) = z_{1}z_{2} + z_{1}z_{3}\).
Just as is the case for real numbers, any non-zero complex number \(z\) has a unique multiplicative inverse, which we may denote by either \(z^{-1}\) or \(1/z\).
Theorem 2.2.6. (continued).
- (Multiplicative Inverses) Given \(z \in \mathbb{C}\) with \(z \neq 0\), there is a unique complex number, denoted \(z^{-1}\), such that \(z z^{-1} = 1\). Moreover, if \(z = (x, y)\) with \(x, y \in \mathbb{R}\), then
\[ z^{-1} = \left(\frac{x}{x^{2} + y^{2}}, \frac{-y}{x^{2} + y^{2}}\right). \]
Proof.
Uniqueness: A complex number \(w\) is an inverse of \(z\) if \(z w=1\) (by the commutativity of complex multiplication this is equivalent to \(w z=1\). We will first prove that if \(w\) and \(v\) are two complex numbers such that \(z w=1\) and \(z v=1\), then we necessarily have \(w=v\). This will then imply that any \(z\in\mathbb{C}\) can have at most one inverse. To see this, we start from \(z v=1\). Multiplying both sides by \(w\), we obtain \(w z v=w 1\). Using the fact that \(1\) is the multiplicative unit, that the product is commutative, and the assumption that \(w\) is an inverse, we get \(z w v=v=w\).
Existence: Now assume \(z\in\mathbb{C}\) with \(z\neq 0\), and write \(z=x+y i\) for \(x,y\in\mathbb{R}\). Since \(z\neq 0\), at least one of \(x\) or \(y\) is not zero, and so \(x^2 + y^2 >0\). Therefore, we can define
\[ w=\left(\frac{x}{x^{2} + y^{2}}, \frac{-y}{x^{2} + y^{2}}\right), \]
and one can check that \(z w=1\).
Now, we can define the division of a complex number \(z_1\) by a non-zero complex number \(z_2\) as the product of \(z_1\) and \(z_2^{-1}\). Explicitly, for two complex numbers \(z_1= x_{1} + i y_{1}\) and \(z_2 =x_{2} +i y_{2}\), we have that their complex quotient is
\[ \frac{z_1}{z_2} = \frac{x_{1}x_{2} + y_{1}y_{2}+ \left(x_{2}y_{1} - x_{1}y_{2}\right)i}{x_{2}^{2} + y_{2}^{2}}. \]
Example 2.2.7. We illustrate the above definition with the following example:
\[
\frac{(1, 2)}{(3, 4)}
=
\left(
\frac{1\cdot 3 + 2\cdot 4}{3^{2} + 4^{2}}
,
\frac{3\cdot 2 - 1\cdot 4}{3^{2} + 4^{2}}
\right)
=
\left(
\frac{3 + 8}{9 + 16}
,
\frac{6 - 4}{9 + 16}
\right)
=
\left(
\frac{11}{25}
,
\frac{2}{25}
\right).
\]
2.2.3 Complex conjugation
Complex conjugation is an operation on \(\mathbb{C}\) that will turn out to be very useful because it allows us to manipulate only the imaginary part of a complex number. In particular, when combined with the notion of modulus (as defined in the next section), it is one of the most fundamental operations on \(\mathbb{C}\). The definition and most basic properties of complex conjugation are as follows. (As in the previous sections, you should provide a proof of the theorem below for your own practice.)
Definition 2.2.8. Given a complex number \(z = (x, y) \in \mathbb{C}\) with \(x, y \in \mathbb{R}\), we define the (complex) conjugate of \(z\) to be the complex number
\[ \bar{z} = (x, -y). \]
Theorem 2.2.9. Given two complex numbers \(z_{1}, z_{2} \in \mathbb{C}\),
- \(\overline{z_{1} + z_{2}} = \overline{z_{1}} + \overline{z_{2}}\).
- \(\overline{z_{1}z_{2}} = \overline{z_{1}}\, \overline{z_{2}}\).
- \( \overline{1/z_1} = 1/\overline{z_1}\), for all \(z_1\neq 0\).
- \(\overline{z_{1}} = z_{1}\) if and only if \(\ImaginaryPart(z_{1}) = 0\).
- \(\overline{\overline{z_{1}}} = z_{1}\).
- the real and imaginary parts of \(z_{1}\) can be expressed as
\[ \mathrm{Re}(z_{1}) = \frac{1}{2}(z_{1} + \overline{z_{1}})
{\rm \quad and \quad}
\mathrm{Im}(z_{1}) = \frac{1}{2 i}(z_1 - \overline{z_1}). \]
2.2.4 The modulus (a.k.a. norm, length, or magnitude)
In this section, we introduce yet another operation on complex numbers, this time based upon a generalization of the notion of absolute value of a real number. To motivate the definition, it is useful to view the set of complex numbers as the two-dimensional Euclidean plane, i.e., to think of \(\mathbb{C}=\mathbb{R}^2\) being equal as sets. The modulus, or length, of \(z\in\mathbb{C}\) is then defined as the Euclidean distance between \(z\), as a point in the plane, and the origin \(0 = (0,0)\). This is the content of the following definition.
Definition 2.2.10. Given a complex number \(z = (x, y) \in \mathbb{C}\) with \(x, y \in \mathbb{R}\), the modulus of \(z\) is defined to be
\[ |z| = \sqrt{x^{2} + y^{2}}. \]
In particular, given \(x \in \mathbb{R}\), note that
\[ | (x, 0) | = \sqrt{x^{2} + 0} = | x | \]
under the convention that the square root function takes on its principal positive value.
Example 2.2.11. Using the above definition, we see that the modulus of the complex number \((3, 4)\) is
\[ | (3, 4) | = \sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5. \]
To see this geometrically, construct a figure in the Euclidean plane, such as
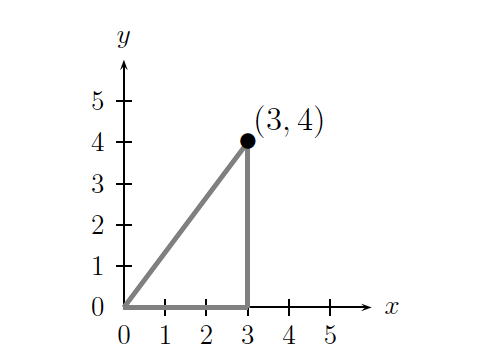
and apply the Pythagorean theorem to the resulting right triangle in order to find the distance from the origin to the point \((3, 4)\).
The following theorem lists the fundamental properties of the modulus, and especially as it relates to complex conjugation. You should provide a proof for your own practice.
Theorem 2.2.12. Given two complex numbers \(z_{1}, z_{2} \in \mathbb{C}\),
- \(|z_{1}z_{2}| = |z_{1}|\cdot|z_{2}|\).
- \({\displaystyle \left|\frac{z_{1}}{z_{2}}\right| = \frac{|z_{1}|}{|z_{2}|}}\), assuming that \(z_{2} \neq 0\).
- \(|\overline{z_{1}}| = |z_{1}|\).
- \(|\mathrm{Re}(z_{1})| \leq |z_{1}|\) and \(|\mathrm{Im}(z_{1})| \leq |z_{1}|\).
- (Triangle Inequality) \(|z_{1} + z_{2}| \leq |z_{1}| + |z_{2}|\).
- (Another Triangle Inequality) \(|z_{1} - z_{2}| \geq |\,|z_{1}| - |z_{2}|\,|\).
- (Formula for Multiplicative Inverse) \(z_{1}\overline{z_{1}} = |z_{1}|^{2}\), from which
\[ z_{1}^{-1} = \frac{\overline{z_{1}}}{|z_{1}|^{2}} \]
when we assume that \(z_{1} \neq 0\).
2.2.5 Complex numbers as vectors in \(\mathbb{R}^{2}\)
When complex numbers are viewed as points in the Euclidean plane \(\mathbb{R}^{2}\), several of the operations defined in Section 2.2 can be directly visualized as if they were operations on vectors.
For the purposes of this chapter, we think of vectors as directed line segments that start at the origin and end at a specified point in the Euclidean plane. These line segments may also be moved around in space as long as the direction (which we will call the argument in Section 2.3.1 below) and the length (a.k.a.~the modulus) are preserved. As such, the distinction between points in the plane and vectors is merely a matter of convention as long as we at least implicitly think of each vector as having been translated so that it starts at the origin.
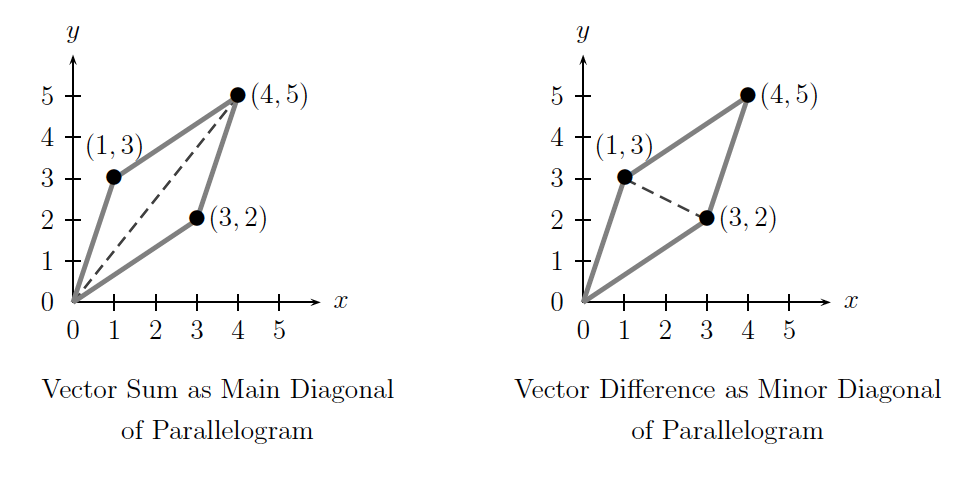
As we saw in Example 2.2.11 above, the modulus of a complex number can be viewed as the length of the hypotenuse of a certain right triangle. The sum and difference of two vectors can also each be represented geometrically as the lengths of specific diagonals within a particular parallelogram that is formed by copying and appropriately translating the two vectors being combined.
Example 2.2.13. We illustrate the sum \((3, 2) + (1, 3) = (4, 5)\) as the main, dashed diagonal of the parallelogram in the left-most figure below. The difference \((3, 2) - (1, 3) = (2, -1)\) can also be viewed as the shorter diagonal of the same parallelogram, though we would properly need to insist that this shorter diagonal be translated so that it starts at the origin. The latter is illustrated in the right-most figure below.
Contributors
- Isaiah Lankham, Mathematics Department at UC Davis
- Bruno Nachtergaele, Mathematics Department at UC Davis
- Anne Schilling, Mathematics Department at UC Davis
Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.