9.3: Orthogonality
- Page ID
- 258
Using the inner product, we can now define the notion of orthogonality, prove that the Pythagorean theorem holds in any inner product space, and use the Cauchy-Schwarz inequality to prove the triangle inequality. In particular, this will show that \(\norm{v}=\sqrt{\inner{v}{v}}\) does indeed define a norm.
Definition 9.3.1. Two vectors \(u,v\in V \) are orthogonal (denoted \(u\bot v\)) if \(\inner{u}{v}=0\).
Note that the zero vector is the only vector that is orthogonal to itself. In fact, the zero vector is orthogonal to every vector \(v\in V\).
Theorem 9.3.2. (Pythagorean Theorem). If \(u,v\in V\), an inner product space, with \(u\bot v\), then \(\norm{\cdot} \) defined by \(\norm{v}:=\sqrt{\inner{v}{v}} \) obeys
\[ \norm{u+v}^2 = \norm{u}^2 + \norm{v}^2. \]
Proof. Suppose \(u,v\in V \) such that \(u\bot v\). Then
\begin{equation*}
\begin{split}
\norm{u+v}^2 &= \inner{u+v}{u+v}
= \norm{u}^2 + \norm{v}^2 + \inner{u}{v} + \inner{v}{u}\\
&= \norm{u}^2 + \norm{v}^2.
\end{split}
\end{equation*}
Note that the converse of the Pythagorean Theorem holds for real vector spaces since, in that case, \(\inner{u}{v}+\inner{v}{u}=2\mathrm{Re} \inner{u}{v} =0\).
Given two vectors \(u,v\in V \) with \(v\neq 0\), we can uniquely decompose \(u \) into two pieces: one piece parallel to \(v \) and one piece orthogonal to \(v\). This is called an orthogonal decomposition. More precisely, we have
\begin{equation*}
u=u_1+u_2,
\end{equation*}
where \(u_1=a v \) and \(u_2\bot v \) for some scalar \(a \in \mathbb{F}\). To obtain such a decomposition, write \(u_2=u-u_1=u-av\). Then, for \(u_2 \) to be
orthogonal to \(v\), we need
\begin{equation*}
0 = \inner{u-av}{v} = \inner{u}{v} - a\norm{v}^2.
\end{equation*}
Solving for \(a \) yields \(a=\inner{u}{v}/\norm{v}^2 \) so that
\begin{equation}\label{eq:orthogonal decomp}
u=\frac{\inner{u}{v}}{\norm{v}^2} v + \left( u-\frac{\inner{u}{v}}{\norm{v}^2} v \right). \tag{9.3.1}
\end{equation}
This decomposition is particularly useful since it allows us to provide a simple proof for the Cauchy-Schwarz inequality.
Theorem 9.3.3 (Cauchy-Schwarz inequality). Given any \(u,v\in V\), we have
\[ |\inner{u}{v}| \le \norm{u} \norm{v}. \]
Furthermore, equality holds if and only if \(u \) and \(v \) are linearly dependent, i.e., are scalar multiples of each other.
Proof. If \(v=0\), then both sides of the inequality are zero. Hence, assume that \(v\neq 0\), and consider the orthogonal decomposition
\begin{equation*}
u = \frac{\inner{u}{v}}{\norm{v}^2} v + w
\end{equation*}
where \(w\bot v\). By the Pythagorean theorem, we have
\begin{equation*}
\norm{u}^2 = \left\| \frac{\inner{u}{v}}{\norm{v}^2}v \right\|^2 + \norm{w}^2
= \frac{|\inner{u}{v}|^2}{\norm{v}^2} + \norm{w}^2 \ge \frac{|\inner{u}{v}|^2}{\norm{v}^2}.
\end{equation*}
Multiplying both sides by \(\norm{v}^2 \) and taking the square root then yields the Cauchy-Schwarz inequality.
Note that we get equality in the above arguments if and only if \(w=0\). But, by Equation (9.3.1), this means that \(u \) and \(v \) are linearly dependent.
The Cauchy-Schwarz inequality has many different proofs. Here is another one.
Alternate Proof of Theorem 9.3.3. Given \(u,v\in V\), consider the norm square of the vector \(u+r e^{i\theta}v:\)
\begin{equation*}
0 \le \norm{u+re^{i\theta}v}^2
= \norm{u}^2 + r^2 \norm{v}^2 + 2 \mathrm{Re} (r e^{i\theta} \inner{u}{v}).
\end{equation*}
Since \( \inner{u}{v} \) is a complex number, one can choose \(\theta \) so that \(e^{i \theta} \inner{u}{v} \) is real. Hence, the right hand side is a parabola \(a r^2 +b r +c \) with real coefficients. It will lie above the real axis, i.e. \(ar^2+br+c\ge 0\), if it does not have any real solutions for \(r\). This is the case when the discriminant satisfies \(b^2-4ac\le 0\). In our case this means
\begin{equation*}
4 | \inner{u}{v} |^2 -4 \norm{u}^2 \norm{v}^2\le 0.
\end{equation*}
Moreover, equality only holds if \(r \) can be chosen such that \(u+r e^{i\theta} v =0\), which means that \(u \) and \(v \) are scalar multiples.
Now that we have proven the Cauchy-Schwarz inequality, we are finally able to verify the triangle inequality. This is the final step in showing that \(\norm{v}=\sqrt{\inner{v}{v}}\) does indeed define a norm. We illustrate the triangle inequality in Figure 9.3.1.
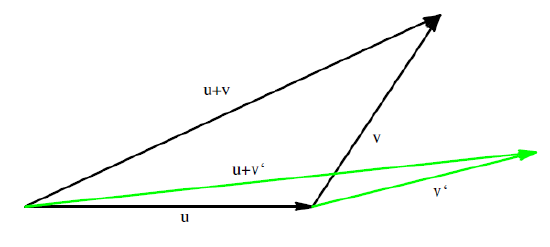
Figure 9.3.1: The Triangle Inequality in \( \mathbb{R^2} \)
Theorem 9.3.4. (Triangle Inequality). For all \(u,v\in V \) we have
\[ \norm{u+v} \le \norm{u} + \norm{v}. \]
Proof. By a straightforward calculation, we obtain
\begin{equation*}
\begin{split}
\norm{u+v}^2 &= \inner{u+v}{u+v} = \inner{u}{u} + \inner{v}{v} +\inner{u}{v} + \inner{v}{u}\\
&= \inner{u}{u} + \inner{v}{v} + \inner{u}{v} +\overline{\inner{u}{v}}
= \norm{u}^2 + \norm{v}^2 +2 \mathrm{Re} \inner{u}{v}.
\end{split}
\end{equation*}
Note that \(\mathrm{Re}\inner{u}{v}\le |\inner{u}{v}| \) so that, using the Cauchy-Schwarz inequality, we obtain
\begin{equation*}
\norm{u+v}^2 \le \norm{u}^2 + \norm{v}^2 + 2\norm{u}\norm{v} = (\norm{u}+\norm{v})^2.
\end{equation*}
Taking the square root of both sides now gives the triangle inequality.
Remark 9.3.5. Note that equality holds for the triangle inequality if and only if \(v=ru \) or \(u=rv \) for some \(r\ge 0\). Namely, equality in the proof happens only if \(\inner{u}{v} =\norm{u}\norm{v}\), which is equivalent to \(u \) and \(v \) being scalar multiples of one another.
Theorem 9.3.6. (Parallelogram Law). Given any \(u,v\in V\), we have
\[ \norm{u+v}^2 + \norm{u-v}^2 = 2(\norm{u}^2 + \norm{v}^2). \]
Proof. By direct calculation,
\begin{equation*}
\begin{split}
\norm{u+v}^2 + \norm{u-v}^2 &= \inner{u+v}{u+v} + \inner{u-v}{u-v}\\
&= \norm{u}^2 + \norm{v}^2 + \inner{u}{v} + \inner{v}{u} + \norm{u}^2 + \norm{v}^2
- \inner{u}{v} -\inner{v}{u}\\
&=2(\norm{u}^2 + \norm{v}^2).
\end{split}
\end{equation*}
Remark 9.3.7. We illustrate the parallelogram law in Figure 9.3.2.
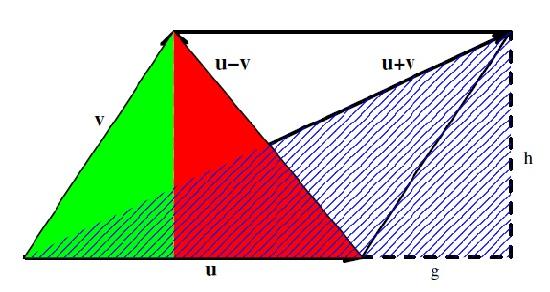
Figure 9.3.2: The Parallelogram Law in \( \mathbb{R^2} \)
Contributors
- Isaiah Lankham, Mathematics Department at UC Davis
- Bruno Nachtergaele, Mathematics Department at UC Davis
- Anne Schilling, Mathematics Department at UC Davis
Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.


