3.6: Second order systems and applications
- Page ID
- 367
Undamped Mass-Spring Systems
While we did say that we will usually only look at first order systems, it is sometimes more convenient to study the system in the way it arises naturally. For example, suppose we have 3 masses connected by springs between two walls. We could pick any higher number, and the math would be essentially the same, but for simplicity we pick 3 right now. Let us also assume no friction, that is, the system is undamped. The masses are \(m_1, m_2\), and \(m_3\) and the spring constants are \(k_1, k_2, k_3\), and \(k_4\). Let \(x_1\) be the displacement from rest position of the first mass, and \(x_2\) and \(x_3\) the displacement of the second and third mass. We will make, as usual, positive values go right (as \(x_1\) grows, the first mass is moving right). See Figure \(\PageIndex{1}\).

This simple system turns up in unexpected places. For example, our world really consists of many small particles of matter interacting together. When we try the above system with many more masses, we obtain a good approximation to how an elastic material behaves. By somehow taking a limit of the number of masses going to infinity, we obtain the continuous one dimensional wave equation (that we study in Section 4.7). But we digress.
Let us set up the equations for the three mass system. By Hooke’s law we have that the force acting on the mass equals the spring compression times the spring constant. By Newton’s second law we have that force is mass times acceleration. So if we sum the forces acting on each mass and put the right sign in front of each term, depending on the direction in which it is acting, we end up with the desired system of equations.
\[\begin{array}{lll}{m_1 x''_1=-k_1 x_1+k_2(x_2-x_1)}&{\quad}&{=-(k_1+k_2)x_1+k_2x_2,} \\ {m_2x''_2=-k_2(x_2-x_1)+k_3(x_3-x_2)}&{\quad}&{=k_2x_1-(k_2+k_3)x_2+k_3x_3,} \\ {m_3x''_3=-k_3(x_3-x_2)-k_4x_3}&{\quad}&{=k_3x_2-(k_3+k_4)x_3.}\end{array} \nonumber \]
We define the matrices
\[ M = \left[ \begin{array}{ccc} m_1 & 0 & 0 \\ 0 & m_2 & 0 \\ 0 & 0 & m_3 \end{array} \right] ~~~{\rm{~and~}}~~~ K= \left[ \begin{array}{ccc} -(k_1+k_2) & k_2 & 0 \\ k_2 & -(k_2+k_3) & k_3 \\ 0 & k_3 & -(k_3+k_4) \end{array} \right]. \nonumber \]
We write the equation simply as
\[M \vec{x}'' = K \vec{x}. \nonumber \]
At this point we could introduce 3 new variables and write out a system of 6 first order equations. We claim this simple setup is easier to handle as a second order system. We call \(\vec{x}\) the displacement vector, \(M\) the mass matrix, and \(K\) the stiffness matrix.
Repeat this setup for 4 masses (find the matrices \( M\) and \(K\)). Do it for 5 masses. Can you find a prescription to do it for \(n\) masses?
As with a single equation we want to “divide by \(M\).” This means computing the inverse of \(M\). The masses are all nonzero and \(M\)is a diagonal matrix, so comping the inverse is easy:
\[ M^{-1}= \left[ \begin{array}{ccc} \frac{1}{m_1} & 0 & 0 \\ 0 & \frac{1}{m_2} & 0 \\ 0 & 0 &\frac{1}{m_3}\end{array} \right]. \nonumber \]
This fact follows readily by how we multiply diagonal matrices. As an exercise, you should verify that \(MM^{-1}=M^{-1}M=I.\)
Let \(A = M^{-1}K\). We look at the system \( \vec{x}'' = M^{-1} K \vec{x}\), or
\[ \vec{x}'' = A \vec{x}. \nonumber \]
Many real world systems can be modeled by this equation. For simplicity, we will only talk about the given masses-and-springs problem. We try a solution of the form
\[ \vec{x} =\vec{v} e^{\alpha t}. \nonumber \]
We compute that for this guess, \( \vec{x}'' =\alpha^2 \vec{v} e^{\alpha t}.\) We plug our guess into the equation and get
\[ \alpha^2 \vec{v} e^{\alpha t} =A \vec{v} e^{\alpha t}. \nonumber \]
We divide by \(e^{\alpha t}\) to arrive at \( \alpha^2 \vec{v}=A\vec{v}\). Hence if \(\alpha^2\) is an eigenvalue of \(A\) and \(\vec{v}\) is a corresponding eigenvector, we have found a solution.
In our example, and in other common applications, \(A\) has only real negative eigenvalues (and possibly a zero eigenvalue). So we study only this case. When an eigenvalue \(\lambda\) is negative, it means that \(\alpha^2= \lambda\) is negative. Hence there is some real number \(\omega\) such that \(-\omega^2 = \lambda\). Then \(\alpha= \pm i \omega\). The solution we guessed was
\[ \vec{x}= \vec{v}(\cos(\omega t) +i \sin(\omega t)). \nonumber \]
By taking the real and imaginary parts (note that \(\vec{v}\) is real), we find that \(\vec{v}\cos(\omega t)\) and \(\vec{v}\sin(\omega t)\) are linearly independent solutions.
If an eigenvalue is zero, it turns out that both \(\vec{v}\) and \(\vec{v}t\) are solutions, where \(\vec{v}\) is an eigenvector corresponding to the eigenvalue 0.
Show that if \(A\) has a zero eigenvalue and \(\vec{v}\) is a corresponding eigenvector, then \(\vec{x}=\vec{v}(a+bt)\) is a solution of \(\vec{x}''=A \vec{x}\) for arbitrary constants \(a\) and \(b\).
Let \(A\) be an \(n \times n\) matrix with \(n\) distinct real negative eigenvalues we denote by \(-\omega_1^2 > -\omega_2^2> \cdots > -\omega_n^2\), and corresponding eigenvectors by \(\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n.\) If \(A\) is invertible (that is, if \(\omega_1>0\)), then
\[ \vec{x}(t)= \sum_{i=1}^{n} \vec{v}_i(a_i \cos (\omega_i t) + b_i \sin (\omega_i t)), \nonumber \]
is the general solution of
\[ \vec{x}''=A \vec{x}, \nonumber \]
for some arbitrary constants \(a_i\) and \(b_i\). If \(A\) has a zero eigenvalue, that is \( \omega_1=0\), and all other eigenvalues are distinct and negative, then the general solution can be written as
\[ \vec{x}(t)= \vec{v}_1(a_1+b_1 t)+ \sum_{i=2}^{n} \vec{v}_i(a_i \cos (\omega_i t) + b_i \sin (\omega_i t)). \nonumber \]
We use this solution and the setup from the introduction of this section even when some of the masses and springs are missing. For example, when there are only 2 masses and only 2 springs, simply take only the equations for the two masses and set all the spring constants for the springs that are missing to zero.
Suppose we have the system in Figure \(\PageIndex{2}\), with \(m_1 = 2, m_2=1, k_1 = 4,\) and \(k_2=2.\)
The equations we write down are
\[ \left[ \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right] \vec{x}''= \left[ \begin{array}{cc} -(4+2) & 2 \\ 2 & -2 \end{array} \right] \vec{x}, \nonumber \]
or
\[ \vec{x}''= \left[ \begin{array}{cc} -3 & 1 \\ 2 & -2 \end{array} \right] \vec{x}. \nonumber \]
We find the eigenvalues of \(A\) to be \(\lambda = -1, -4\) (exercise). We find corresponding eigenvectors to be \(\left[ \begin{array}{c} 1 \\ 2 \end{array} \right]\) and \(\left[ \begin{array}{c} 1 \\ -1 \end{array} \right]\) respectively (exercise).
We check the theorem and note that \(\omega_1=1\) and \(\omega_2=2\). Hence the general solution is
\[ \vec{x}= \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] (a_1 \cos (t) + b_1 \sin (t)) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] (a_2 \cos (2t) + b_2 \sin (2t)). \nonumber \]
The two terms in the solution represent the two so-called natural or normal modes of oscillation. And the two (angular) frequencies are the natural frequencies. The first natural frequency is \(1\), and second natural frequency is \(2\). The two modes are plotted in Figure \(\PageIndex{3}\).
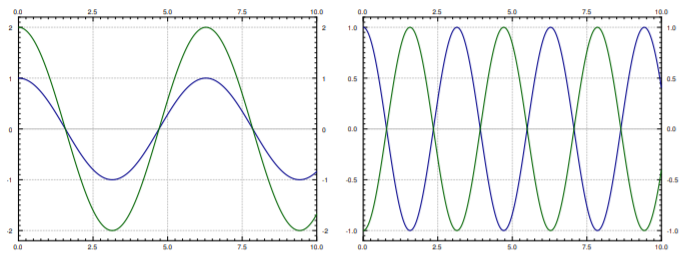
Let us write the solution as
\[ \vec{x}= \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] c_1 \cos (t-\alpha_1) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] c_2 \cos (2t- \alpha_2). \nonumber \]
The first term,
\[ \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] c_1 \cos (t-\alpha_1) = \left[ \begin{array}{c} c_1 \cos (t-\alpha_1) \\ 2c_1 \cos (t-\alpha_1) \end{array} \right], \nonumber \]
corresponds to the mode where the masses move synchronously in the same direction.
The second term,
\[ \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] c_2 \cos (2t-\alpha_2) = \left[ \begin{array}{c} c_2 \cos (2t-\alpha_2) \\ -c_2 \cos (2t-\alpha_2) \end{array} \right], \nonumber \]
corresponds to the mode where the masses move synchronously but in opposite directions.
The general solution is a combination of the two modes. That is, the initial conditions determine the amplitude and phase shift of each mode. As an example, suppose we have initial conditions
\[\vec{x}(0) = \begin{bmatrix} 1 \\ -1 \end{bmatrix} , \qquad \vec{x}'(0) = \begin{bmatrix} 0 \\ 6 \end{bmatrix} . \nonumber \]
We use the \(a_j, b_j\) constants to solve for initial conditions. First
\[\begin{bmatrix} 1 \\ -1 \end{bmatrix} = \vec{x}(0) = \begin{bmatrix} 1 \\ 2 \end{bmatrix} a_1 + \begin{bmatrix} 1 \\ -1 \end{bmatrix} a_2 = \begin{bmatrix} a_1+a_2 \\2a_1 - a_2 \end{bmatrix} . \nonumber \]
We solve (exercise) to find \(a_1 = 0\), \(a_2 = 1\). To find the \(b_1\) and \(b_2\), we differentiate first: \[{\vec{x}}' = \begin{bmatrix} 1 \\ 2 \end{bmatrix} \bigl( - a_1 \sin (t) + b_1 \cos (t) \bigr) + \begin{bmatrix} 1 \\ -1 \end{bmatrix} \bigl( - 2a_2 \sin (2t) + 2 b_2 \cos (2t) \bigr) . \nonumber \]
Now we solve: \[\begin{bmatrix} 0 \\ 6 \end{bmatrix} = {\vec{x}}'(0) = \begin{bmatrix} 1 \\ 2 \end{bmatrix} b_1 + \begin{bmatrix} 1 \\ -1 \end{bmatrix} 2 b_2 = \begin{bmatrix} b_1+2b_2 \\ 2b_1-2b_2 \end{bmatrix} . \nonumber \]
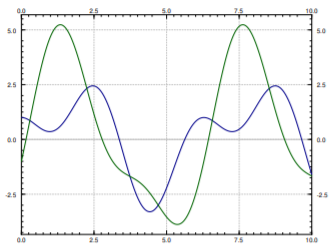
Again solve (exercise) to find \(b_1 = 2\), \(b_2 = -1\). So our solution is \[\vec{x} = \begin{bmatrix} 1 \\ 2 \end{bmatrix} 2 \sin (t) + \begin{bmatrix} 1 \\ -1 \end{bmatrix} \bigl( \cos (2t) - \sin (2t) \bigr) = \begin{bmatrix} 2 \sin (t) + \cos(2t)- \sin(2t) \\ 4 \sin (t) - \cos(2t) + \sin(2t) \end{bmatrix} . \nonumber \]
The graphs of the two displacements, \(x_1\) and \(x_2\) of the two carts is in Figure \(\PageIndex{4}\).
We have two toy rail cars. Car 1 of mass \(2\text{ kg}\) is traveling at \(3\:\frac{\text{m}}{\text{s}}\) towards the second rail car of mass \(1\text{ kg}\). There is a bumper on the second rail car that engages at the moment the cars hit (it connects to two cars) and does not let go. The bumper acts like a spring of spring constant \(k=2\:\frac{\text{N}}{\text{m}}\). The second car is \(10\) meters from a wall. See Figure \(\PageIndex{5}\).
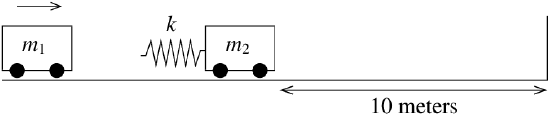
We want to ask several questions. At what time after the cars link does impact with the wall happen? What is the speed of car 2 when it hits the wall?
OK, let us first set the system up. Let \(t=0\) be the time when the two cars link up. Let \(x_1\) be the displacement of the first car from the position at \(t=0\), and let \(x_2\) be the displacement of the second car from its original location. Then the time when \(x_2(t)=10\) is exactly the time when impact with wall occurs. For this \(t,x'_2(t)\) is the speed at impact. This system acts just like the system of the previous example but without \(k_1\). Hence the equation is
\[ \left[ \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right] \vec{x}''= \left[ \begin{array}{cc} -2 & 2 \\ 2 & -2 \end{array} \right] \vec{x}. \nonumber \]
or
\[ \vec{x}''= \left[ \begin{array}{cc} -1 & 1 \\ 2 & -2 \end{array} \right] \vec{x}. \nonumber \]
We compute the eigenvalues of \(A\). It is not hard to see that the eigenvalues are \(0\) and \(-3\) (exercise). Furthermore, eigenvectors are \(\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]\) and \(\left[ \begin{array}{c} 1 \\ -2 \end{array} \right]\) respectively (exercise). Then \(\omega_2= \sqrt{3}\) and by the second part of the theorem we find our general solution to be
\[ \begin{align}\begin{aligned} \vec{x}&= \left[ \begin{array}{c} 1 \\ 1 \end{array} \right](a_1+b_1t) + \left[ \begin{array}{c} 1 \\ -2 \end{array} \right](a_2 \cos(\sqrt3 t)+ b_2 \sin(\sqrt3 t)) \\ &=\left[ \begin{array}{c} a_1 + b_1t+a_2 \cos(\sqrt3 t)+ b_2 \sin(\sqrt3 t) \\ a_1+ b_1t- 2a_2 \cos(\sqrt3 t)- 2b_2 \sin(\sqrt3 t) \end{array} \right]\end{aligned}\end{align} \nonumber \]
We now apply the initial conditions. First the cars start at position \(0\) so \(x_1(0)=0\) and \(x_2(0)=0\). The first car is traveling at \(3\:\frac{\text{m}}{\text{s}}\), so \(x'_1(0)=3\) and the second car starts at rest, so \(x'_2(0)=0\). The first conditions says
\[ \vec{0} = \vec{x}(0)= \left[ \begin{array}{c} a_1+ a_2 \\ a_1-2a_2 \end{array} \right]. \nonumber \]
It is not hard to see that \(a_1=a_2=0\). We set \(a_1=0\) and \(a_2=0\) in \(\vec{x}(t)\) and differentiate to get
\[ \vec{x}'(t)= \left[ \begin{array}{c} b_1+ \sqrt3 b_2 \cos(\sqrt3 t)\\ b_1- 2 \sqrt3 b_2 \cos(\sqrt3 t) \end{array} \right]. \nonumber \]
So
\[ \left[ \begin{array}{c} 3\\ 0 \end{array} \right] = \vec{x}'(0)= \left[ \begin{array}{c} b_1+ \sqrt3 b_2 \\ b_1- 2 \sqrt3 b_2 \end{array} \right]. \nonumber \]
Solving these two equations we find \(b_1 = 2\) and \(b_2 = \frac{1}{\sqrt3}\). Hence the position of our cars is (until the impact with the wall)
\[ \vec{x}= \left[ \begin{array}{c} 2t +\frac{1}{\sqrt3} \sin(\sqrt3 t) \\ 2t -\frac{2}{\sqrt3} \sin(\sqrt3 t)\end{array} \right] . \nonumber \]
Note how the presence of the zero eigenvalue resulted in a term containing \(t\). This means that the carts will be traveling in the positive direction as time grows, which is what we expect.
What we are really interested in is the second expression, the one for \(x_2\). We have \(x_2(t)= 2t -\frac{2}{\sqrt3} \sin(\sqrt3 t)\). See Figure \(\PageIndex{6}\) for the plot of \(x_2\) versus time.
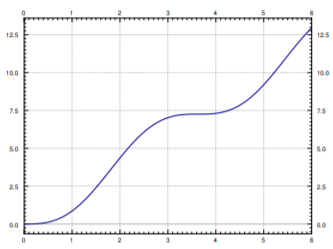
Just from the graph we can see that time of impact will be a little more than 5 seconds from time zero. For this we have to solve the equation \(10=x_{2}(t)=2t-\frac{2}{\sqrt{3}}\sin (\sqrt{3}t)\). Using a computer (or even a graphing calculator) we find that \(t_{\text{impact}}\approx 5.22\) seconds.
As for the speed we note that \(x'_2 = 2-2 \cos(\sqrt3 t)\). At time of impact (\(5.22\) seconds from \(t=0\)) we get that \( x'_2(t_{\rm{impact}}) \approx 3.85\).
The maximum speed is the maximum of \(2-2 \cos(\sqrt3 t)\), which is \(4\). We are traveling at almost the maximum speed when we hit the wall.
Suppose that Bob is a tiny person sitting on car 2. Bob has a Martini in his hand and would like not to spill it. Let us suppose Bob would not spill his Martini when the first car links up with car 2, but if car 2 hits the wall at any speed greater than zero, Bob will spill his drink. Suppose Bob can move car 2 a few meters towards or away from the wall (he cannot go all the way to the wall, nor can he get out of the way of the first car). Is there a “safe” distance for him to be at? A distance such that the impact with the wall is at zero speed?
The answer is yes. Looking at Figure \(\PageIndex{6}\), we note the “plateau” between \(t=3\) and \(t=4\). There is a point where the speed is zero. To find it we need to solve \(x'_2(t)=0\). This is when \(\cos(\sqrt3 t) = 1\) or in other words when \(t=\frac{2 \pi}{\sqrt3}, \frac{4 \pi}{\sqrt3}, \ldots\) and so on. We plug in the first value to obtain \( x_2 \left( \frac{2 \pi}{\sqrt3} \right)=\frac{4 \pi}{\sqrt3} \approx 7.26 \). So a “safe” distance is about 7 and a quarter meters from the wall.
Alternatively Bob could move away from the wall towards the incoming car 2 where another safe distance is \( \frac{8 \pi}{\sqrt3 } \approx 14.51\) and so on, using all the different \(t\) such that \(x'_2(t)=0\). Of course \(t=0\) is always a solution here, corresponding to \(x_2=0\), but that means standing right at the wall.
Forced Oscillations
Finally we move to forced oscillations. Suppose that now our system is
\[\label{eq:30} \vec{x}'' = A \vec{x} + \vec{F} \cos(\omega t). \]
That is, we are adding periodic forcing to the system in the direction of the vector \(\vec{F}\).
As before, this system just requires us to find one particular solution \(\vec{x}_p\), add it to the general solution of the associated homogeneous system \(\vec{x}_c\), and we will have the general solution to \(\eqref{eq:30}\). Let us suppose that \(\omega\) is not one of the natural frequencies of \( \vec{x}'' = A \vec{x}\), then we can guess
\[ \vec{x}_p= \vec{c} \cos(\omega t), \nonumber \]
where \(\vec{c}\) is an unknown constant vector. Note that we do not need to use sine since there are only second derivatives. We solve for \(\vec{c}\) to find \(\vec{x}_p\). This is really just the method of undetermined coefficients for systems. Let us differentiate \(\vec{x}_p\) twice to get
\[ \vec{x}''_p= -\omega^2 \vec{c} \cos(\omega t). \nonumber \]
Plug \(\vec{x}_p\) and \(\vec{x}''_p\) into the equation \(\eqref{eq:30}\):
\[\overbrace{ -\omega^2 \vec{c} \cos (\omega t) }^{{\vec{x}_p}''} = \overbrace{ A \vec{c} \cos (\omega t) }^{A \vec{x}_p} + \vec{F} \cos (\omega t) . \nonumber \]
We cancel out the cosine and rearrange the equation to obtain
\[ (A + \omega^2 I) \vec{c} = - \vec{F}. \nonumber \]
So
\[ \vec{c} = (A + \omega^2 I)^{-1} (- \vec{F}). \nonumber \]
Of course this is possible only if \( (A + \omega^2 I)= (A -(- \omega^2) I)\) is invertible. That matrix is invertible if and only if \(- \omega^2\) is not an eigenvalue of \(A\). That is true if and only if \(\omega\) is not a natural frequency of the system.
We simplified things a little bit. If we wish to have the forcing term to be in the units of force, say Newtons, then we must write \[M \vec{x}'' = K \vec{x} + \vec{G} \cos(\omega t) . \nonumber \]
If we then write things in terms of \(A = M^{-1} K\), we have \[\vec{x}'' = M^{-1}K \vec{x} + M^{-1} \vec{G} \cos(\omega t) \qquad \text{or} \qquad \vec{x}'' = A \vec{x} + \vec{F} \cos(\omega t) , \nonumber \]
where \(\vec{F} = M^{-1} \vec{G}\).
Let us take the example in Figure \(\PageIndex{2}\) with the same parameters as before: \(m_1=2, m_2=1, k_1= 4,\) and \(k_2=2\). Now suppose that there is a force \( 2 \cos(3t)\) acting on the second cart.
The equation is
\[\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} {\vec{x}}'' = \begin{bmatrix} -4 & 2 \\ 2 & -2 \end{bmatrix} \vec{x} + \begin{bmatrix} 0 \\ 2 \end{bmatrix} \cos (3 t) \qquad \text{or} \qquad {\vec{x}}'' = \begin{bmatrix} -3 & 1 \\ 2 & -2 \end{bmatrix} \vec{x} + \begin{bmatrix} 0 \\ 2 \end{bmatrix} \cos (3 t) . \nonumber \]
We solved the associated homogeneous equation before and found the complementary solution to be
\[ \vec{x}_c= \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] (a_1 \cos(t) + b_1 \sin(t)) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] (a_2 \cos(2t) + b_2 \sin(2t)). \nonumber \]
The natural frequencies are \(1\) and \(2\). Hence as \(3\) is not a natural frequency, we can try \( \vec{c} \cos(3t)\). We invert \((A+3^2 I)\):
\[ \left( \left[ \begin{array}{cc} -3 & 1 \\ 2 & -2 \end{array} \right] + 3^2 I \right)^{-1}= \left[ \begin{array}{cc} 6 & 1 \\ 2 & 7 \end{array} \right]^{-1}= \left[ \begin{array}{cc} \frac{7}{40} & \frac{-1}{40} \\ \frac{-1}{20} & \frac{3}{20} \end{array} \right]. \nonumber \]
Hence,
\[ \vec{c}= (A+\omega^2 I)^{-1} (- \vec{F})= \left[ \begin{array}{cc} \frac{7}{40} & \frac{-1}{40} \\ \frac{-1}{20} & \frac{3}{20} \end{array} \right] \left[ \begin{array}{c} 0 \\ -2 \end{array} \right] = \left[ \begin{array}{c} \frac{1}{20} \\ \frac{-3}{10} \end{array} \right]. \nonumber \]
Combining with what we know the general solution of the associated homogeneous problem to be, we get that the general solution to \(\vec{x}''= A \vec{x} +\vec{F} \cos(\omega t)\) is
\[ \vec{x} = \vec{x}_c + \vec{x}_p = \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] (a_1 \cos(t) + b_1 \sin(t)) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] (a_2 \cos(2t) + b_2 \sin(2t)) + \left[ \begin{array}{c} \frac{1}{20} \\ \frac{-3}{10} \end{array} \right] \cos(3t). \nonumber \]
The constants \(a_1, a_2, b_1,\) and \(b_2\) must then be solved for given any initial conditions.
Note that given force \(\vec{f}\), we write the equation as \(M\vec{x}''=K\vec{x}+\vec{f}\) to get the units right. Then we write \(\vec{x}''=M^{-1}K\vec{x}+M^{-1}\vec{f}\). The term \(\vec{g}=M^{-1}\vec{f}\) in \(\vec{x}''=A\vec{x}+\vec{g}\) is in units of force per unit mass.
If \(\omega\) is a natural frequency of the system resonance occurs because we will have to try a particular solution of the form
\[ \vec{x}_p = \vec{c}t \sin(\omega t)+ \vec{d}t \cos(\omega t) . \nonumber \]
That is assuming that the eigenvalues of the coefficient matrix are distinct. Next, note that the amplitude of this solution grows without bound as \(t\) grows.


