4.10: Dirichlet Problem in the Circle and the Poisson Kernel
- Page ID
- 341
Laplace in Polar Coordinates
A more natural setting for the Laplace equation \( \Delta u=0\) is the circle rather than the square. On the other hand, what makes the problem somewhat more difficult is that we need polar coordinates.
Recall that the polar coordinates for the \((x,y)\)-plane are \((r, \theta )\):
\[ x= r \cos \theta, ~~~~ y= r \sin \theta, \nonumber \]
where \(r \geq 0\) and \(- \pi < \theta < \pi\). So \((x,y)\) is distance \(r\) from the origin at angle \( \theta\) from the positive \(x\)-axis.
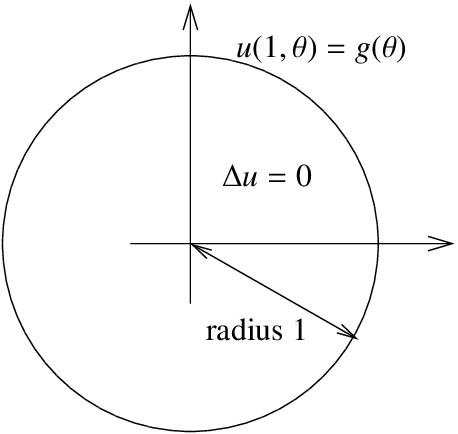
Now that we know our coordinates, let us give the problem we wish to solve. We have a circular region of radius 1, and we are interested in the Dirichlet problem for the Laplace equation for this region. Let \(u(r, \theta )\) denote the temperature at the point \((r, \theta )\) in polar coordinates. We have the problem:
\[ \begin{align} \Delta u &=0, & {\rm{for~}} r<1, \label{eq:2} \\ u(1, \theta ) &=g( \theta), &{\rm{for~}} \pi < \theta \leq \pi . \end{align} \nonumber \]
The first issue we face is that we do not know what the Laplacian is in polar coordinates. Normally we would find \(u_{xx}\) and \(u_{yy}\) in terms of the derivatives in \(r\) and \(\theta\). We would need to solve for \(r\) and \(\theta\) in terms of \(x\) and \(y\). While this is certainly possible, it happens to be more convenient to work in reverse. Let us instead compute derivatives in \(r\) and \(\theta\) in terms of derivatives in \(x\) and \(y\) and then solve. The computations are easier this way. First
\[\begin{align}\begin{aligned} x_r &= \cos \theta, &x_{\theta}= -r \sin \theta, \\ y_{r} &= \sin \theta, & y_{\theta}= r \cos \theta . \end{aligned}\end{align} \nonumber \]
Next by chain rule we obtain
\[\begin{align}\begin{aligned} u_r &=u_xx_{r}+u_yy_{r}= \cos(\theta)u_x + \sin(\theta)u_y, \\ u_{rr} &= \cos(\theta)(u_{xx}x_r+u_{xy}y_r)+ \sin(\theta)(u_{yx}x_r+u_{yy}y_r) \\ &= \cos^2(\theta)u_{xx}+2 \cos(\theta) \sin(\theta)u_{xy}+ \sin^2(\theta)u_{yy}.\end{aligned}\end{align} \nonumber \]
Similarly for the \(\theta\) derivative. Note that we have to use product rule for the second derivative.
\[\begin{align}\begin{aligned} u_{\theta} &=u_xx_{\theta}+u_yy_{\theta}= -r \sin(\theta)u_x + r \cos(\theta)u_y, \\ u_{\theta \theta} &= -r \cos(\theta)(u_x)- r \sin(\theta)(u_{xx}x_{\theta}+u_{xy}y_{\theta})-r \sin(\theta)(u_y)+r \cos(\theta)(u_{yx}x_{\theta}+u_{yy}y_{\theta}) \\ &= -r \cos(\theta)u_{x}-r \sin(\theta)u_y+r^2 \sin^2(\theta)u_{xx}-r^2 2 \sin(\theta) \cos(\theta) u_{xy}+r^2 \cos^2(\theta)u_{yy}.\end{aligned}\end{align} \nonumber \]
Let us now try to solve for \(u_{xx}+u_{yy}\). We start with \( \frac{1}{r^2}u_{\theta \theta}\) to get rid of those pesky \(r^2\). If we add \(u_{rr}\) and use the fact that \(\cos^2(\theta)+ \sin^2(\theta)=1\), we get
\[ \frac{1}{r^2}u_{\theta \theta} +u_{rr}=u_{xx}+u_{yy}- \frac{1}{r} \cos(\theta)u_x- \frac{1}{r} \sin(\theta)u_y. \nonumber \]
We’re not quite there yet, but all we are lacking is \( \frac{1}{r}u_r\). Adding it we obtain the Laplacian in polar coordinates:
\[ \frac{1}{r^2}u_{\theta \theta}+ \frac{1}{r}u_{r}+u_{rr}=u_{xx}+u_{yy}= \Delta u. \nonumber \]
Notice that the Laplacian in polar coordinates no longer has constant coefficients.
Series Solution
Let us separate variables as usual. That is let us try \(u(r, \theta)=R(r) \Theta ( \theta)\). Then
\[0= \Delta u=\frac{1}{r^2}R \Theta''+ \frac{1}{r}R' \Theta+R'' \Theta . \nonumber \]
Let us put \(R\) on one side and \( \Theta\) on the other and conclude that both sides must be constant.
\[\begin{align}\begin{aligned} \frac{1}{r^2}R \Theta'' &= - \left( \frac{1}{r}R'+R'' \right) \Theta . \\ \frac{ \Theta''}{ \Theta} &= - \frac{rR'+r^2R''}{R} + - \lambda.\end{aligned}\end{align} \nonumber \]
We get two equations:
\[\begin{align}\begin{aligned} \Theta''+\lambda \Theta &=0, \\ r^2R''+rR'- \lambda R &=0.\end{aligned}\end{align} \nonumber \]
Let us first focus on \( \Theta\). We know that \(u(r, \theta)\) ought to be \(2 \pi\)-periodic in \( \theta\), that is, \(u(r, \theta)=u(r, \theta +2 \pi)\). Therefore, the solution to \( \Theta''+\lambda \Theta=0\) must be \(2 \pi\)-periodic. We have seen such a problem in Example 4.1.5. We conclude that \(\lambda=n^2\) for a nonnegative integer \(n=0,1,2,3,...\). The equation becomes \( \Theta''+n^2 \Theta=0\). When \(n=0\) the equation is just \( \Theta''=0\), so we have the general solution \(A \theta+B\). As \( \Theta\) is periodic, \(A=0\). For convenience let us write this solution as
\[\Theta_0=\frac{a_0}{2} \nonumber \]
for some constant \(a_0\). For positive \(n\), the solution to \( \Theta''+n^2 \Theta=0\) is
\[ \Theta_n=a_n \cos(n \theta)+b_n \sin(n \theta), \nonumber \]
for some constants \(a_n\) and \(b_n\).
Next, we consider the equation for \(R\),
\[r^2R''+rR'-n^2R=0. \nonumber \]
This equation has appeared in exercises before—we solved it in Exercise 2.E.2.1.6 and Exercise 2.E.1.7. The idea is to try a solution \(r^s\) and if that does not work out try a solution of the form \(r^s \ln r\). When \(n=0\) we obtain
\[R_0=Ar^0+Br^0 \ln r=A+B \ln r, \nonumber \]
and if \(n>0\), we get
\[ R_n=Ar^n+Br^{-n}. \nonumber \]
The function \(u(r, \theta)\) must be finite at the origin, that is, when \(r=0\). Therefore, \(B=0\) in both cases. Let us set \(A=1\) in both cases as well, the constants in \( \Theta_n\) will pick up the slack so we do not lose anything. Therefore let
\[ R_0=1,\quad\text{and}\quad R_n=r^n. \nonumber \]
Hence our building block solutions are
\[u_0(r, \theta)= \frac{a_0}{2},\quad u_n(r, \theta)=a_n r^n \cos(n \theta)+b_n r^n \sin(n \theta). \nonumber \]
Putting everything together our solution is:
\[u(r, \theta)= \frac{a_0}{2}+ \sum_{n=1}^{\infty}a_n r^n \cos(n \theta)+b_n r^n \sin(n \theta). \nonumber \]
We look at the boundary condition in \(\eqref{eq:2}\),
\[g(\theta)=u(1, \theta)= \frac{a_0}{2}+ \sum_{n=1}^{\infty}a_n \cos(n \theta)+b_n \sin(n \theta). \nonumber \]
Therefore, the solution \(\eqref{eq:2}\) is to expand \(g(\theta)\), which is a \(2 \pi\)-periodic function as a Fourier series, and then the \(n^{\text{th}}\) coordinate is multiplied by \(r^n\). In other words, to compute \(a^n\) and \(b^n\) from the formula we can, as usual, compute
\[a_n= \frac{1}{ \pi} \int_{ \pi}^{- \pi} g(\theta) \cos(n \theta)d \theta, \quad\text{and}\quad b_n= \frac{1}{ \pi} \int_{ \pi}^{- \pi} g(\theta) \sin(n \theta)d \theta. \nonumber \]
Suppose we wish to solve
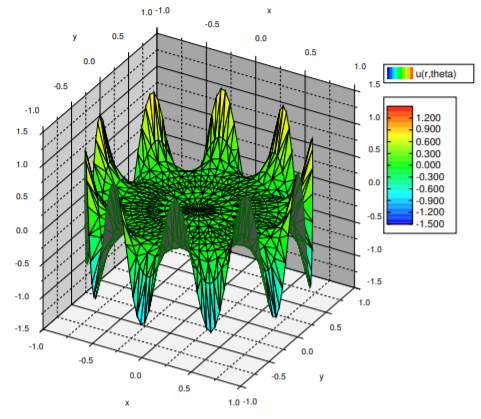
\[\begin{align}\begin{aligned} & \Delta u = 0 , \qquad 0 \leq r < 1, \quad -\pi < \theta \leq \pi,\\ & u(1,\theta) = \cos(10\,\theta), \qquad -\pi < \theta \leq \pi.\end{aligned}\end{align} \nonumber \]
The solution is
\[ u(r, \theta)=r^{10} \cos(10 \theta). \nonumber \]
See the plot in Figure \(\PageIndex{3}\). The thing to notice in this example is that the effect of a high frequency is mostly felt at the boundary. In the middle of the disc, the solution is very close to zero. That is because \(r^{10}\) rather small when \(r\) is close to \(0\).
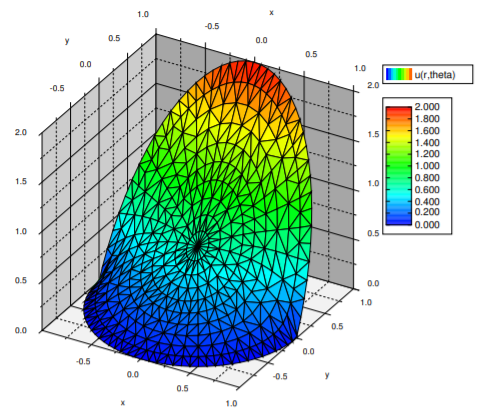
Let us solve a more difficult problem. Suppose we have a long rod with circular cross section of radius \(1\) and we wish to solve the steady state heat problem. If the rod is long enough we simply need to solve the Laplace equation in two dimensions. Let us put the center of the rod at the origin and we have exactly the region we are currently studying—a circle of radius \(1\). For the boundary conditions, suppose in Cartesian coordinates \(x\) and \(y\), the temperature is fixed at \(0\) when \(y<0\) and at \(2y\) when \(y>0\).
We set the problem up. As \(y=r \sin(\theta)\), then on the circle of radius \(1\) we have \(2y=2 \sin(\theta)\). So
\[\begin{align}\begin{aligned} & \Delta u = 0 , \qquad 0 \leq r < 1, \quad -\pi < \theta \leq \pi,\\ & u(1,\theta) = \begin{cases} 2\sin(\theta) & \text{if } \; \phantom{-}0 \leq \theta \leq \pi, \\ 0 & \text{if } \; {-\pi} < \theta < 0. \end{cases}\end{aligned}\end{align} \nonumber \]
We must now compute the Fourier series for the boundary condition. By now the reader has plentiful experience in computing Fourier series and so we simply state that
\[ u(1, \theta)= \frac{2}{\pi}+ \sin(\theta)+ \sum_{n=1}^{\infty} \frac{-4}{\pi (4n^2-1)} \cos(2n \theta). \nonumber \]
Compute the series for \(u(1, \theta)\) and verify that it really is what we have just claimed. Hint: Be careful, make sure not to divide by zero.
We now simply write the solution (see Figure \(\PageIndex{4}\)) by multiplying by \(r^n\) in the right places.
\[ u(r, \theta)= \frac{2}{\pi}+ r\sin(\theta)+ \sum_{n=1}^{\infty} \frac{-4r^{2n}}{\pi (4n^2-1)} \cos(2n \theta). \nonumber \]
Poisson Kernel
There is another way to solve the Dirichlet problem with the help of an integral kernel. That is, we will find a function \(P(r,\theta,\alpha)\) called the Poisson kernel\(^{1}\) such that
\[u(r,\theta)= \frac{1}{2\pi} \int_{-\pi}^{\pi}P(r,\theta,\alpha)g(\alpha)d\alpha. \nonumber \]
While the integral will generally not be solvable analytically, it can be evaluated numerically. In fact, unless the boundary data is given as a Fourier series already, it will be much easier to numerically evaluate this formula as there is only one integral to evaluate.
The formula also has theoretical applications. For instance, as \(P(r,\theta,\alpha)\) will have infinitely many derivatives, then via differentiating under the integral we find that the solution \(u(r,\theta)\) has infinitely many derivatives, at least when inside the circle, \(r<1\). By infinitely many derivatives what you should think of is that \(u(r,\theta)\) has “no corners” and all of its partial derivatives exist too and also have “no corners”.
We will compute the formula for \(P(r,\theta,\alpha)\) from the series solution, and this idea can be applied anytime you have a convenient series solution where the coefficients are obtained via integration. Hence you can apply this reasoning to obtain such integral kernels for other equations, such as the heat equation. The computation is long and tedious, but not overly difficult. Since the ideas are often applied in similar contexts, it is good to understand how this computation works.
What we do is start with the series solution and replace the coefficients with the integrals that compute them. Then we try to write everything as a single integral. We must use a different dummy variable for the integration and hence we use \(\alpha\) instead of \(\theta\).
\[\begin{align}\begin{aligned} u(r,\theta )&=\frac{a_{0}}{2}+\sum\limits_{n=1}^\infty a_{n}r^{n}\cos (n\theta )+b_{n}r^{n}\sin (n\theta ) \\ &=\underset{\frac{a_{0}}{2}}{\underbrace{\left(\frac{1}{2\pi}\int_{-\pi}^{\pi}g(\alpha )d\alpha\right)}}+\sum\limits_{n=1}^\infty \underset{a_{n}}{\underbrace{\left(\frac{1}{\pi}\int_{-\pi}^{\pi}g(\alpha)\cos (n\alpha )d\alpha\right)}}r^{n}\cos (n\theta) \\ &+\underset{b_{n}}{\underbrace{\left(\frac{1}{\pi}\int_{-\pi}^{\pi}g(\alpha)\sin (n\alpha)d\alpha\right)}}r^{n}\sin (n\theta ) \\ &=\frac{1}{2\pi}\int_{-\pi}^{\pi}\left(g(\alpha)+2\sum\limits_{n=1}^\infty g(\alpha)\cos (n\alpha)r^{n}\cos (n\theta )+g(\alpha )\sin (n\alpha )r^{n}\sin (n\theta )\right) d\alpha \\ &=\frac{1}{2\pi}\int_{-\pi}^{\pi}\underset{P(r,\theta ,\alpha )}{\underbrace{\left( 1+2\sum\limits_{n=1}^\infty r^{n}\left(\cos (n\alpha )\cos (n\theta )+\sin (n\alpha )\sin (n\theta )\right)\right)}}g(\alpha )d\alpha \end{aligned}\end{align} \nonumber \]
OK, so we have what we wanted, the expression in the parentheses is the Poisson kernel, \(P(r,\theta,\alpha)\). However, we can do a lot better. It is still given as a series, and we would really like to have a nice simple expression for it. We must work a little harder. The trick is to rewrite everything in terms of complex exponentials. Let us work just on the kernel.
\[\begin{align}\begin{aligned} P(r,\theta,\alpha) &=1+2\sum_{n=1}^{\infty}r^n(\cos(n\alpha)\cos(n\theta)+ \sin(n\alpha)\sin(n\theta)) \\ &= 1+2\sum_{n=1}^{\infty}r^n \cos(n(\theta- \alpha)) \\ &= 1+2\sum_{n=1}^{\infty}r^n(e^{in(\theta-\alpha)}+e^{-in(\theta-\alpha)}) \\ &= 1+\sum_{n=1}^{\infty}(re^{i(\theta-\alpha)})^n+\sum_{n=1}^{\infty}(re^{-i(\theta-\alpha)})^n.\end{aligned}\end{align} \nonumber \]
In the above expression we recognize the geometric series. That is, recall from calculus that as long as \( |z|<1\), then
\[\sum_{n=1}^{\infty}z^n= \frac{z}{1-z}. \nonumber \]
Note that \(n\) starts at \(1\) and that is why we have the \(z\) in the numerator. It is the standard geometric series multiplied by \(z\). Let us continue with the computation.
\[\begin{align}\begin{aligned} P(r,\theta,\alpha) &=1+\sum_{n=1}^{\infty}(re^{i(\theta-\alpha)})^n+\sum_{n=1}^{\infty}(re^{-i(\theta-\alpha)})^n \\ &= 1+ \frac{re^{i(\theta-\alpha)}}{1-re^{i(\theta-\alpha)}}+ \frac{re^{-i(\theta-\alpha)}}{1-re^{-i(\theta-\alpha)}} \\ &=\frac{(1-re^{i(\theta-\alpha)})(1-re^{-i(\theta-\alpha)})+(1-re^{-i(\theta-\alpha)})re^{ i(\theta-\alpha)}+(1-re^{i(\theta-\alpha)})re^{ - i(\theta-\alpha)}}{(1-re^{i(\theta-\alpha)})(1-re^{-i(\theta-\alpha)})} \\ &= \frac{1-r^2}{1-re^{i(\theta-\alpha)}-re^{-i(\theta-\alpha)}+r^2} \\ &= \frac{1-r^2}{1-2r\cos(\theta-\alpha)+r^2}.\end{aligned}\end{align} \nonumber \]
Now that’s a formula we can live with. The solution to the Dirichlet problem using the Poisson kernel is
\[u(r, \theta)= \frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{1-r^2}{1-2r\cos(\theta-\alpha)+r^2}g(\alpha)d\alpha. \nonumber \]
Sometimes the formula for the Poisson kernel is given together with the constant \(\frac{1}{2\pi}\), in which case we should of course not leave it in front of the integral. Also, often the limits of the integral are given as \(0\) to \(2\pi\); everything inside is \(2\pi\)-periodic in \(\alpha\), so this does not change the integral.
Let us not leave the Poisson kernel without explaining its geometric meaning. Let \(s\) be the distance from \((r,\theta)\) to \((1,\alpha)\). You may recall from calculus that this distance \(s\) in polar coordinates is given precisely by the square root of \(1-2r\cos(\theta-\alpha)+r^2\). That is, the Poisson kernel is really the formula
\[\frac{1-r^2}{s^2}. \nonumber \]
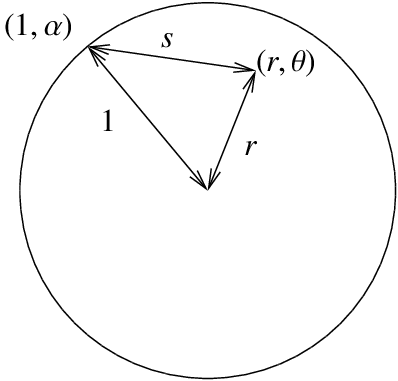
One final note we make about the formula is to note that it is really a weighted average of the boundary values. First let us look at what happens at the origin, that is when \(r=0\).
\[\begin{align}\begin{aligned} u(0,0) &= \frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{1-0^2}{1-2(0)\cos(\theta-\alpha)+0^2}g(\alpha)d\alpha \\ &= \frac{1}{2\pi} \int_{-\pi}^{\pi} g(\alpha)d\alpha. \end{aligned}\end{align} \nonumber \]
So \(u(0,0)\) is precisely the average value of \(g(\theta)\) and therefore the average value of \(u\) on the boundary. This is a general feature of harmonic functions, the value at some point \(p\) is equal to the average of the values on a circle centered at \(p\).
What the formula says is that the value of the solution at any point in the circle is a weighted average of the boundary data \(g(\theta)\). The kernel is bigger when \((r,\theta)\) is closer to \((1,\alpha)\). Therefore when computing \(u(r,\theta)\) we give more weight to the values \(g(\alpha)\) when \((1,\alpha)\) is closer to \((r,\theta)\) and less weight to the values \(g(\theta)\) when \((1,\alpha)\) far from \((r,\theta)\).
Footnotes
[1] Named for the French mathematician Siméon Denis Poisson (1781 – 1840).


