5.3: Steady Periodic Solutions
- Page ID
- 328
Forced Vibrating String
Consider a guitar string of length \(L\). We studied this setup in Section 4.7. Let \(x\) be the position on the string, \(t\) the time, and \(y\) the displacement of the string. See Figure \(\PageIndex{1}\).
The problem is governed by the equations
\[\label{eq:1} \begin{array}{ll} y_{tt} = a^2 y_{xx} , & \\ y(0,t) = 0 , & y(L,t) = 0 , \\ y(x,0) = f(x) , & y_t(x,0) = g(x) . \end{array} \]
We saw previously that the solution is of the form
\[ y= \sum_{n=1}^{\infty} \left( A_n\cos \left( \frac{n\pi a}{L}t \right) + B_n\sin \left( \frac{n\pi a}{L}t \right) \right) \sin \left( \frac{n\pi }{L}x \right), \nonumber \]
where \(A_n\) and \(B_n\) were determined by the initial conditions. The natural frequencies of the system are the (circular) frequencies \(\frac{n\pi a}{L}\) for integers \(n \geq 1\).
But these are free vibrations. What if there is an external force acting on the string. Let us assume say air vibrations (noise), for example a second string. Or perhaps a jet engine. For simplicity, assume nice pure sound and assume the force is uniform at every position on the string. Let us say \(F(t)=F_0 \cos(\omega t)\) as force per unit mass. Then our wave equation becomes (remember force is mass times acceleration)
\[\label{eq:3} y_{tt}=a^2y_{xx}+F_0\cos(\omega t), \]
with the same boundary conditions of course.
We want to find the solution here that satisfies the above equation and
\[\label{eq:4} y(0,t)=0,~~~~~y(L,t)=0,~~~~~y(x,0)=0,~~~~~y_t(x,0)=0. \]
That is, the string is initially at rest. First we find a particular solution \(y_p\) of \(\eqref{eq:3}\) that satisfies \(y(0,t)=y(L,t)=0\). We define the functions \(f\) and \(g\) as
\[f(x)=-y_p(x,0),~~~~~g(x)=- \frac{\partial y_p}{\partial t}(x,0). \nonumber \]
We then find solution \(y_c\) of \(\eqref{eq:1}\). If we add the two solutions, we find that \(y=y_c+y_p\) solves \(\eqref{eq:3}\) with the initial conditions.
Check that \(y=y_c+y_p\) solves \(\eqref{eq:3}\) and the side conditions \(\eqref{eq:4}\).
So the big issue here is to find the particular solution \(y_p\). We look at the equation and we make an educated guess
\[y_p(x,t)=X(x)\cos(\omega t). \nonumber \]
We plug in to get
\[ - \omega^2X\cos(\omega t)=a^2X''\cos(\omega t), \nonumber \]
or \(- \omega X=a^2X''+F_0\) after canceling the cosine. We know how to find a general solution to this equation (it is a nonhomogeneous constant coefficient equation). The general solution is
\[ X(x)=A\cos \left( \frac{\omega}{a}x \right)+B\sin \left( \frac{\omega}{a}x \right)- \frac{F_0}{\omega^2}. \nonumber \]
The endpoint conditions imply \(X(0)=X(L)=0\). So
\[ 0=X(0)=A- \frac{F_0}{\omega^2}, \nonumber \]
or \(A=\frac{F_0}{\omega^2}\), and also
\[ 0=X(L)= \frac{F_0}{\omega^2} \cos \left( \frac{\omega L}{a} \right)+B\sin \left( \frac{\omega L}{a} \right)- \frac{F_0}{\omega^2}. \nonumber \]
Assuming that \(\sin \left( \frac{\omega L}{a} \right) \) is not zero we can solve for \(B\) to get
\[\label{eq:11} B=\frac{-F_0 \left( \cos \left( \frac{\omega L}{a} \right)-1 \right)}{- \omega^2 \sin \left( \frac{\omega L}{a} \right)}. \]
Therefore,
\[ X(x)= \frac{F_0}{\omega^2} \left( \cos \left( \frac{\omega}{a}x \right)- \frac{ \cos \left( \frac{\omega L}{a} \right)-1 }{ \sin \left( \frac{\omega L}{a} \right)}\sin \left( \frac{\omega}{a}x \right)-1 \right). \nonumber \]
The particular solution \(y_p\) we are looking for is
\[ y_p(x,t)= \frac{F_0}{\omega^2} \left( \cos \left( \frac{\omega}{a}x \right)- \frac{ \cos \left( \frac{\omega L}{a} \right)-1 }{ \sin \left( \frac{\omega L}{a} \right)}\sin \left( \frac{\omega}{a}x \right)-1 \right) \cos(\omega t). \nonumber \]
Check that \(y_p\) works.
Now we get to the point that we skipped. Suppose that \(\sin \left( \frac{\omega L}{a} \right)=0\). What this means is that \(\omega\) is equal to one of the natural frequencies of the system, i.e. a multiple of \( \frac{\pi a}{L}\). We notice that if \(\omega\) is not equal to a multiple of the base frequency, but is very close, then the coefficient \(B\) in \(\eqref{eq:11}\) seems to become very large. But let us not jump to conclusions just yet. When \(\omega = \frac{n\pi a}{L}\) for \(n\) even, then \(\cos \left( \frac{\omega L}{a} \right)=1\) and hence we really get that \(B=0\). So resonance occurs only when both \(\cos \left( \frac{\omega L}{a} \right)=-1\) and \(\sin \left( \frac{\omega L}{a} \right)=0\). That is when \(\omega = \frac{n\pi a}{L}\) for odd \(n\).
We could again solve for the resonance solution if we wanted to, but it is, in the right sense, the limit of the solutions as \(\omega\) gets close to a resonance frequency. In real life, pure resonance never occurs anyway.
The above calculation explains why a string will begin to vibrate if the identical string is plucked close by. In the absence of friction this vibration would get louder and louder as time goes on. On the other hand, you are unlikely to get large vibration if the forcing frequency is not close to a resonance frequency even if you have a jet engine running close to the string. That is, the amplitude will not keep increasing unless you tune to just the right frequency.
Similar resonance phenomena occur when you break a wine glass using human voice (yes this is possible, but not easy\(^{1}\)) if you happen to hit just the right frequency. Remember a glass has much purer sound, i.e. it is more like a vibraphone, so there are far fewer resonance frequencies to hit.
When the forcing function is more complicated, you decompose it in terms of the Fourier series and apply the above result. You may also need to solve the above problem if the forcing function is a sine rather than a cosine, but if you think about it, the solution is almost the same.
Let us do the computation for specific values. Suppose \(F_0=1\) and \(\omega =1\) and \(L=1\) and \(a=1\). Then
\[ y_p(x,t)= \left( \cos(x)- \frac{ \cos(1)-1 }{ \sin(1)}\sin(x)-1 \right) \cos(t). \nonumber \]
Write \(B= \frac{ \cos(1)-1 }{ \sin(1)} \) for simplicity.
Then plug in \(t=0\) to get
\[f(x)=-y_p(x,0)=- \cos x+B \sin x+1, \nonumber \]
and after differentiating in \( t\) we see that \(g(x)=- \frac{\partial y_P}{\partial t}(x,0)=0\).
Hence to find \(y_c\) we need to solve the problem
\[\begin{align}\begin{aligned} & y_{tt} = y_{xx} , \\ & y(0,t) = 0 , \quad y(1,t) = 0 , \\ & y(x,0) = - \cos x + B \sin x +1 , \\ & y_t(x,0) = 0 .\end{aligned}\end{align} \nonumber \]
Note that the formula that we use to define \(y(x,0)\) is not odd, hence it is not a simple matter of plugging in to apply the D’Alembert formula directly! You must define \(F\) to be the odd, 2-periodic extension of \(y(x,0)\). Then our solution would look like
\[\label{eq:17} y(x,t)= \frac{F(x+t)+F(x-t)}{2}+ \left( \cos(x) - \frac{\cos(1)-1}{\sin(1)}\sin(x)-1 \right) \cos(t). \]
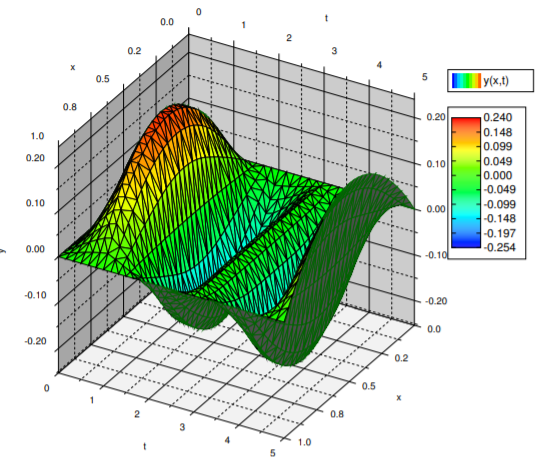
It is not hard to compute specific values for an odd extension of a function and hence \(\eqref{eq:17}\) is a wonderful solution to the problem. For example it is very easy to have a computer do it, unlike a series solution. A plot is given in Figure \(\PageIndex{2}\).
Underground Temperature Oscillations
Let \(u(x,t)\) be the temperature at a certain location at depth \(x\) underground at time \(t\). See Figure \(\PageIndex{3}\).
The temperature \(u\) satisfies the heat equation \(u_t=ku_{xx}\), where \(k\) is the diffusivity of the soil. We know the temperature at the surface \(u(0,t)\) from weather records. Let us assume for simplicity that
\[ u(0,t)=T_0+A_0 \cos(\omega t), \nonumber \]
where \(T_0\) is the yearly mean temperature, and \(t=0\) is midsummer (you can put negative sign above to make it midwinter if you wish). \(A_0\) gives the typical variation for the year. That is, the hottest temperature is \(T_0+A_0\) and the coldest is \(T_0-A_0\). For simplicity, we will assume that \(T_0=0\). The frequency \(\omega\) is picked depending on the units of \(t\), such that when \(t=1\), then \(\omega t=2\pi\). For example if \(t\) is in years, then \(\omega=2\pi\).
It seems reasonable that the temperature at depth \(x\) will also oscillate with the same frequency. This, in fact, will be the steady periodic solution, independent of the initial conditions. So we are looking for a solution of the form
\[ u(x,t)=V(x)\cos(\omega t)+ W(x)\sin(\omega t). \nonumber \]
for the problem
\[\label{eq:20} u_t=ku_{xx,}~~~~~~u(0,t)=A_0\cos(\omega t). \]
We will employ the complex exponential here to make calculations simpler. Suppose we have a complex valued function
\[h(x,t)=X(x)e^{i \omega t}. \nonumber \]
We will look for an \(h\) such that \({\rm Re} h=u\). To find an \(h\), whose real part satisfies \(\eqref{eq:20}\), we look for an \(h\) such that
\[\label{eq:22} h_t=kh_{xx,}~~~~~~h(0,t)=A_0 e^{i \omega t}. \]
Suppose \(h\) satisfies \(\eqref{eq:22}\). Use Euler’s formula for the complex exponential to check that \(u={\rm Re}\: h\) satisfies \(\eqref{eq:20}\).
Substitute \(h\) into \(\eqref{eq:22}\).
\[ i \omega Xe^{i \omega t}=kX''e^{i \omega t}. \nonumber \]
Hence,
\[ kX''-i \omega X=0, \nonumber \]
or
\[ X''- \alpha^2 X=0, \nonumber \]
where \( \alpha = \pm \sqrt{\frac{i \omega }{k}}\). Note that \(\pm \sqrt{i}= \pm \frac{1=i}{\sqrt{2}}\) so you could simplify to \( \alpha= \pm (1+i) \sqrt{\frac{\omega}{2k}}\). Hence the general solution is
\[ X(x)=Ae^{-(1+i)\sqrt{\frac{\omega}{2k}x}}+Be^{(1+i)\sqrt{\frac{\omega}{2k}x}}. \nonumber \]
We assume that an \(X(x)\) that solves the problem must be bounded as \(x \rightarrow \infty\) since \(u(x,t)\) should be bounded (we are not worrying about the earth core!). If you use Euler’s formula to expand the complex exponentials, you will note that the second term will be unbounded (if \(B \neq 0\)), while the first term is always bounded. Hence \(B=0\).
Use Euler’s formula to show that \(e^{(1+i)\sqrt{\frac{\omega}{2k}x}}\) is unbounded as \(x \rightarrow \infty\), while \(e^{-(1+i)\sqrt{\frac{\omega}{2k}x}}\) is bounded as \(x \rightarrow \infty\).
Furthermore, \(X(0)=A_0\) since \(h(0,t)=A_0e^{i \omega t}\). Thus \(A=A_0\). This means that
\[ h(x,t)=A_0e^{-(1+i)\sqrt{\frac{\omega}{2k}x}}e^{i \omega t}=A_0e^{-(1+i)\sqrt{\frac{\omega}{2k}}x+i \omega t}=A_0e^{- \sqrt{\frac{\omega}{2k}}x}e^{i( \omega t- \sqrt{\frac{\omega}{2k}}x)}. \nonumber \]
We will need to get the real part of \(h\), so we apply Euler’s formula to get
\[ h(x,t)=A_0e^{- \sqrt{\frac{\omega}{2k}}x} \left( \cos \left( \omega t - \sqrt{\frac{\omega}{2k}x} \right) +i \sin \left( \omega t - \sqrt{\frac{\omega}{2k}x} \right) \right). \nonumber \]
Then finally
\[u(x,t)={\rm Re}h(x,t)=A_0e^{- \sqrt{\frac{\omega}{2k}}x} \cos \left( \omega t- \sqrt{\frac{\omega}{2k}}x \right). \nonumber \]
Yay!
Notice the phase is different at different depths. At depth the phase is delayed by \(x \sqrt{\frac{\omega}{2k}}\). For example in cgs units (centimeters-grams-seconds) we have \(k=0.005\) (typical value for soil), \(\omega = \frac{2\pi}{\text{seconds in a year}}=\frac{2\pi}{31,557,341}\approx 1.99\times 10^{-7}\). Then if we compute where the phase shift \(x\sqrt{\frac{\omega}{2k}}=\pi\) we find the depth in centimeters where the seasons are reversed. That is, we get the depth at which summer is the coldest and winter is the warmest. We get approximately \(700\) centimeters, which is approximately \(23\) feet below ground.
Be careful not to jump to conclusions. The temperature swings decay rapidly as you dig deeper. The amplitude of the temperature swings is \(A_0e^{- \sqrt{\frac{\omega}{2k}}x}\). This function decays very quickly as \(x\) (the depth) grows. Let us again take typical parameters as above. We will also assume that our surface temperature swing is \(\pm 15^{\circ}\) Celsius, that is, \(A_0=15\). Then the maximum temperature variation at \(700\) centimeters is only \(\pm 0.66^{\circ}\) Celsius.
You need not dig very deep to get an effective “refrigerator,” with nearly constant temperature. That is why wines are kept in a cellar; you need consistent temperature. The temperature differential could also be used for energy. A home could be heated or cooled by taking advantage of the above fact. Even without the earth core you could heat a home in the winter and cool it in the summer. The earth core makes the temperature higher the deeper you dig, although you need to dig somewhat deep to feel a difference. We did not take that into account above.
Footnotes
[1] Mythbusters, episode 31, Discovery Channel, originally aired may 18th 2005.


