7.4.2: Green's Function and Conformal Mapping
- Page ID
- 2190
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
For two-dimensional domains there is a beautiful connection between conformal mapping and Green's function. Let \(w=f(z)\) be a conformal mapping from a sufficiently regular connected domain in \(\mathbb{R}^2\) onto the interior of the unit circle, see Figure 7.4.2.1
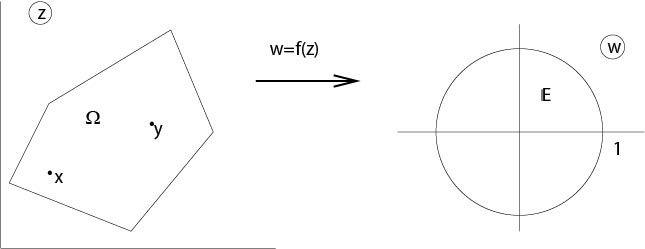
Figure 7.4.2.1: Conformal mapping
Then the Green function of \(\Omega\) is, see for example [16] or other text books about the theory of functions of one complex variable,
$$
G(z,z_0)=\frac{1}{2\pi}\ln\left|\frac{1-f(z)\overline{f(z_0)}}{f(z)-f(z_0)}\right|,
$$
where \(z=x_1+ix_2\), \(z_0=y_1+iy_2\).
Contributors and Attributions
Integrated by Justin Marshall.


