2.1: Linear Equations
- Page ID
- 2133
Let us begin with the linear homogeneous equation
\begin{equation}
\label{homtwo}
a_1(x,y)u_x+a_2(x,y)u_y=0.
\end{equation}
Assume there is a \(C^1\)-solution \(z=u(x,y)\). This function defines a surface \(S\) which has at \(P=(x,y,u(x,y))\) the normal
$$
{\bf N}=\frac{1}{\sqrt{1+|\nabla u|^2}}(-u_x,-u_y,1)
$$
and the tangential plane defined by
$$
\zeta-z=u_x(x,y)(\xi-x)+u_y(x,y)(\eta-y).
$$
Set \(p=u_x(x,y)\), \(q=u_y(x,y)\) and \(z=u(x,y)\). The tuple \((x,y,z,p,q)\) is called surface element and the tuple \((x,y,z)\) support of the surface element. The tangential plane is defined by the surface element. On the other hand, differential equation (\ref{homtwo})
$$
a_1(x,y)p+a_2(x,y)q=0
$$
defines at each support \((x,y,z)\) a bundle of planes if we consider all \((p,q)\) satisfying this equation. For fixed \((x,y)\), this family of planes \(\Pi(\lambda)=\Pi(\lambda;x,y)\) is defined by a one parameter family of ascents \(p(\lambda)=p(\lambda;x,y)\), \(q(\lambda)=q(\lambda;x,y)\).
The envelope of these planes is a line since
$$
a_1(x,y)p(\lambda)+a_2(x,y)q(\lambda)=0,
$$
which implies that the normal \({\bf N}(\lambda)\) on \(\Pi(\lambda)\) is perpendicular on \((a_1,a_2,0)\).
Consider a curve \({\bf x}(\tau)=(x(\tau),y(\tau),z(\tau))\) on \(\mathcal S\), let
\(T_{{\bf x}_0}\) be the tangential plane at \({\bf x}_0=(x(\tau_0),y(\tau_0),z(\tau_0))\) of \(\mathcal S\)
and consider on \(T_{{\bf x}_0}\) the line
$$
L:\ \ l(\sigma)={\bf x}_0+\sigma{\bf x}'(\tau_0),\ \ \sigma\in\mathbb{R}^1,
$$
see Figure 2.1.1.
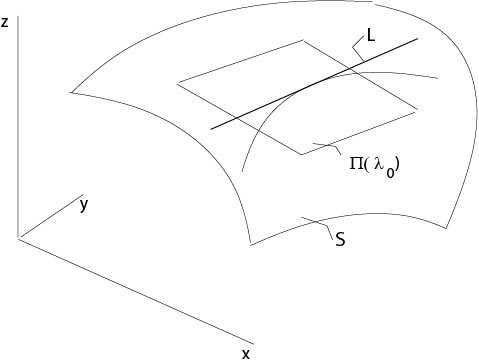
Figure 2.1.1: Curve on a surface
We assume \(L\) coincides with the envelope, which is a line here, of the family of planes \(\Pi(\lambda)\) at \((x,y,z)\). Assume that \(T_{{\bf x}_0}=\Pi(\lambda_0)\) and consider two planes
\begin{eqnarray*}
\Pi(\lambda_0):\ \ \ z-z_0&=&(x-x_0)p(\lambda_0)+(y-y_0)q(\lambda_0)\\
\Pi(\lambda_0+h):\ \ \ z-z_0&=&(x-x_0)p(\lambda_0+h)+(y-y_0)q(\lambda_0+h).
\end{eqnarray*}
At the intersection \(l(\sigma)\) we have
$$
(x-x_0)p(\lambda_0)+(y-y_0)q(\lambda_0)=(x-x_0)p(\lambda_0+h)+(y-y_0)q(\lambda_0+h).
$$
Thus,
$$
x'(\tau_0)p'(\lambda_0)+y'(\tau_0)q'(\lambda_0)=0.
$$
From the differential equation
$$
a_1(x(\tau_0),y(\tau_0))p(\lambda)+a_2(x(\tau_0),y(\tau_0))q(\lambda)=0
$$
it follows
$$
a_1p'(\lambda_0)+a_2q'(\lambda_0)=0.
$$
Consequently
$$
(x'(\tau),y'(\tau))=\frac{x'(\tau)}{a_1(x(\tau,y(\tau))}(a_1(x(\tau),y(\tau)),a_2(x(\tau),y(\tau)),
$$
since \(\tau_0\) was an arbitrary parameter. Here we assume that \(x'(\tau)\not=0\) and \(a_1(x(\tau),y(\tau))\not=0\).
Then we introduce a new parameter \(t\) by the inverse of \(\tau=\tau(t)\), where
$$
t(\tau)=\int_{\tau_0}^\tau \frac{x'(s)}{a_1(x(s),y(s))}\ ds.
$$
It follows \(x'(t)=a_1(x,y),\ y'(t)=a_2(x,y)\). We denote \({\bf x}(\tau(t))\) by \({\bf x}(t)\) again.
Now we consider the initial value problem
\begin{equation}
\label{chartwo}
x'(t)=a_1(x,y),\ \ y'(t)=a_2(x,y),\ \ x(0)=x_0,\ y(0)=y_0.
\end{equation}
From the theory of ordinary differential equations it follows (Theorem of Picard-Lindelöf) that there is a unique solution in a neighbourhood of \(t=0\) provided the functions \(a_1,\ a_2\) are in \(C^1\). From this definition of the curves \((x(t),y(t))\) is follows that
the field of directions \((a_1(x_0,y_0),a_2(x_0,y_0))\) defines the slope of these curves at \((x(0),y(0))\).
Definition. The differential equations in (\ref{chartwo}) are called characteristic equations or characteristic system and solutions of the associated initial value problem are called characteristic curves.
Definition. A function \(\phi(x,y)\) is said to be an integral of the characteristic system if \(\phi(x(t),y(t))=const.\) for each characteristic curve. The constant depends on the characteristic curve considered.
Proposition 2.1. Assume \(\phi\in C^1\) is an integral, then \(u=\phi(x,y)\) is a solution of (\ref{homtwo}).
Proof. Consider for given \((x_0,y_0)\) the above initial value problem (\ref{chartwo}). Since \(\phi(x(t),y(t))=const.\) it follows
$$
\phi_xx'+\phi_yy'=0
$$
for $ |t|<t_0$, \(t_0>0\) and sufficiently small.
Thus
$$
\phi_x(x_0,y_0)a_1(x_0,y_0)+\phi_y(x_0,y_0)a_2(x_0,y_0)=0.
\]
\(\Box\)
Remark. If \(\phi(x,y)\) is a solution of equation (\ref{homtwo}) then also \(H(\phi(x,y))\), where \(H(s)\) is a given \(C^1\)-function.
Examples
Example 2.1.1:
Consider
$$
a_1u_x+a_2u_y=0,
$$
where \(a_1,\ a_2\) are constants. The system of characteristic equations is
$$
x'=a_1,\ y'=a_2.
$$
Thus the characteristic curves are parallel straight lines defined by
$$
x=a_1t+A,\ y=a_2t+B,
$$
where \(A,\ B\) are arbitrary constants. From these equations it follows that
$$
\phi(x,y):=a_2x-a_1y
$$
is constant along each characteristic curve. Consequently, see Proposition 2.1, \(u=a_2x-a_1y\) is a solution of the differential equation. From an exercise it follows that
\begin{equation}
\label{cyl}
u=H(a_2x-a_1y),
\end{equation}
where \(H(s)\) is an arbitrary \(C^1\)-function, is also a solution. Since \(u\) is constant when \(a_2x-a_1y\) is constant, equation (\ref{cyl}) defines cylinder surfaces which are generated by parallel straight lines which are parallel to the \((x,y)\)-plane, see Figure 2.1.2.
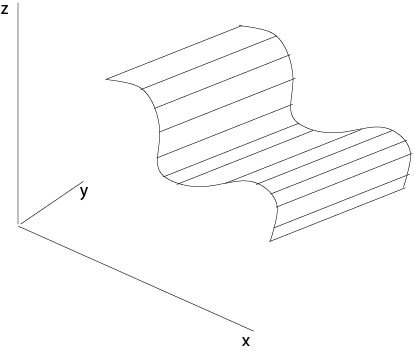
Figure 2.1.2: Cylinder surfaces
Example 2.1.2:
Consider the differential equation
$$
xu_x+yu_y=0.
$$
The characteristic equations are
$$
x'=x,\ y'=y,
$$
and the characteristic curves are given by
$$
x=Ae^t,\ y=Be^t,
$$
where \(A,\ B\) are arbitrary constants. Then an integral is \(y/x\), \(x\not=0\), and for a given \(C^1\)-function the function \(u=H(x/y)\) is a solution of the differential equation. If \(y/x=const.\), then \(u\) is constant. Suppose that \(H'(s)>0\), for example, then \(u\) defines right helicoids (in German: Wendelflächen), see Figure 2.1.3.

Figure 2.1.3: Right helicoid, \(a^2<x^2+y^2<R^2\) (Museo Ideale Leonardo da Vinci, Italy)
Example 2.1.3:
Consider the differential equation
$$
yu_x-xu_y=0.
$$
The associated characteristic system is
$$
x'=y,\ y'=-x.
$$
If follows
$$
x'x+yy'=0,
$$
or, equivalently,
$$
\frac{d}{dt}(x^2+y^2)=0,
$$
which implies that \(x^2+y^2=const.\) along each characteristic. Thus, rotationally symmetric surfaces defined by \(u=H(x^2+y^2)\), where \(H'\not=0\), are solutions of the differential equation.
Example 2.1.4:
The associated characteristic equations to
$$
ayu_x+bxu_y=0,
$$
where \(a,\ b\) are positive constants,
are given by
$$
x'=ay,\ y'=bx.
$$
It follows \(bxx'-ayy'=0\), or equivalently,
$$
\frac{d}{dt}(bx^2-ay^2)=0.
$$
Solutions of the differential equation are \(u=H(bx^2-ay^2)\), which define surfaces which have a hyperbola as the intersection with planes parallel to the \((x,y)\)-plane. Here \(H(s)\) is an arbitrary \(C^1\)-function, \(H'(s)\not=0\).
Contributors and Attributions
Integrated by Justin Marshall.


