7.4.1: Green's Function for a Ball
- Page ID
- 2189
If \(\Omega=B_R(0)\) is a ball, then Green's function is explicitly known.
Let \(\Omega=B_R(0)\) be a ball in \(\mathbb{R}^n\) with radius \(R\) and the center at the origin. Let \(x,\ y\in B_R(0)\) and let \(y'\) the reflected point of \(y\) on the sphere \(\partial B_R(0)\), that is, in particular \(|y||y'|=R^2\), see Figure 7.4.1.1 for notations.
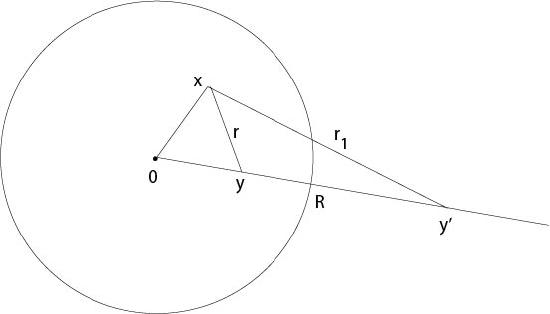
Figure 7.4.1.1: Reflection on \(\partial B_R(0)\)
Set
$$G(x,y)=s(r)-s\left(\frac{\rho}{R}r_1\right),\]
where \(s\) is the singularity function of Section 7.1, \(r=|x-y|\) and
$$\rho^2=\sum_{i=1}^ny_i^2,\ \ \ r_1=\sum_{i=1}^n\left(x_i-\frac{R^2}{\rho^2}y_i\right)^2.\]
This function \(G(x,y)\) satisfies (i)-(iii) of the definition of a Green function. We claim that
$$u(x)=-\int_{\partial B_R(0)} \frac{\partial}{\partial n_y}G(x,y)\Phi\ dS_y\]
is a solution of the Dirichlet problem (7.3.1.1), (7.3.1.2). This formula is also true for a large class of domains \(\Omega\subset\mathbb{R}^n\), see [13].
Lemma.
$$-\frac{\partial}{\partial n_y}G(x,y)\bigg|_{|y|=R}=\frac{1}{R\omega_n}\frac{R^2-|x|^2}{|y-x|^n}.\]
Proof. Exercise.
Set
\begin{equation}
\label{ell13}\tag{7.4.1.1}
H(x,y)=\frac{1}{R\omega_n}\frac{R^2-|x|^2}{|y-x|^n},
\end{equation}
which is called Poisson's kernel.
Theorem 7.2. Assume \(\Phi\in C(\partial\Omega)\). Then
$$u(x)=\int_{\partial B_R(0)}\ H(x,y)\Phi(y)\ dS_y$$
is the solution of the first boundary value problem (7.3.1.1), (7.3.1.2) in the class \(C^2(\Omega)\cap C(\overline{\Omega})\).
Proof. The proof follows from following properties of \(H(x,y)\):
- \(H(x,y)\in C^\infty,\ \ |y|= R,\ |x|<R,\ x\not=y\),
- \(\triangle_xH(x,y)=0,\ \ |x|<R,\ |y|=R\),
- \(\int_{\partial B_R(0)}\ H(x,y)\ dS_y=1,\ \ |x|<R\),
- \(H(x,y)>0,\ \ |y|=R,\ |x|<R\),
- Fix \(\zeta\in\partial B_R(0)\) and \(\delta>0\), then \(\lim_{x\to\zeta,|x|<R}H(x,y)=0\) uniformly in \(y\in\partial B_R(0),\ |y-\zeta|>\delta\).
(i), (iv) and (v) follow from the definition (\ref{ell13}) of \(H\) and (ii) from (\ref{ell13}) or from
$$H=-\frac{\partial G(x,y)}{\partial n_y}\bigg|_{y\in\partial B_R(0)},\]
\(G\) harmonic and \(G(x,y)=G(y,x)\).
Property (iii) is a consequence of formula
$$u(x)=\int_{\partial B_R(0)}\ H(x,y)u(y)\ dS_y,\]
for each harmonic function \(u\), see calculations to the representation formula above. We obtain (ii) if we set \(u\equiv1\).
It remains to show that \(u\), given by Poisson's formula, is in \(C(\overline{B_R(0)})\) and that \(u\) achieves the prescribed boundary values. Fix \(\zeta\in \partial B_R(0)\) and let \(x\in B_R(0)\). Then
\begin{eqnarray*}
u(x)-\Phi(\zeta)&=&\int_{\partial B_R(0)}\ H(x,y)\left(\Phi(y)-\Phi(\zeta)\right)\ dS_y\\
&=& I_1+I_2,
\end{eqnarray*}
where
\begin{eqnarray*}
I_1&=&\int_{\partial B_R(0),\ |y-\zeta|<\delta}\ H(x,y)\left(\Phi(y)-\Phi(\zeta)\right)\ dS_y\\
I_2&=&\int_{\partial B_R(0),\ |y-\zeta|\ge\delta}\ H(x,y)\left(\Phi(y)-\Phi(\zeta)\right)\ dS_y.\\
\end{eqnarray*}
For given (small) \(\epsilon>0\) there is a \(\delta=\delta(\epsilon)>0\) such that
$$|\Phi(y)-\Phi(\zeta)|<\epsilon\]
for all \(y\in\partial B_R(0)\) with \(|y-\zeta|<\delta\). It follows \(|I_1|\le\epsilon\) because of (iii) and (iv). Set \(M=\max_{\partial B_R(0)}|\phi|\). From (v) we conclude that there is a \(\delta'>0\) such that
$$H(x,y)<\frac{\epsilon}{2M\omega_nR^{n-1}}\]
if \(x\) and \(y\) satisfy \(|x-\zeta|<\delta',\ |y-\zeta|>\delta\), see Figure 7.4.1.2 for notations.
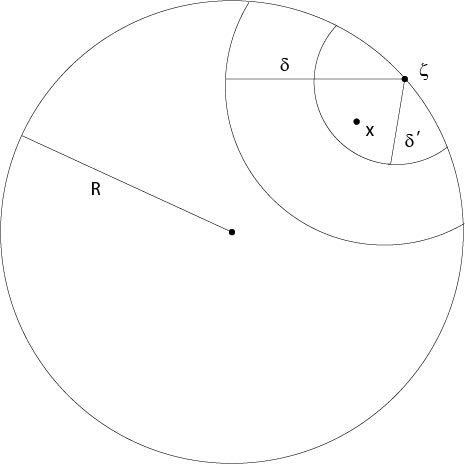
Figure 7.4.1.2: Proof of Theorem 7.2
Thus \(|I_2|<\epsilon\) and the inequality
$$|u(x)-\Phi(\zeta)|<2\epsilon\]
for \(x\in B_R(0)\) such that \(|x-\zeta|<\delta'\) is shown.
\(\Box\)
Remark. Define \(\delta\in[0,\pi]\) through \(\cos\delta=x\cdot y/(|x||y|)\), then we write Poisson's formula of Theorem 7.2 as
$$u(x)=\frac{R^2-|x|^2}{\omega_nR}\int_{\partial B_R(0)}\Phi(y)\frac{1}{\left(|x|^2+R^2-2|x|R\cos\delta\right)^{n/2}}\ dS_y.\]
In the case \(n=2\) we can expand this integral in a power series with respect to \(\rho:=|x|/R\) if \(|x|<R\), since
\begin{eqnarray*}
\frac{R^2-|x|^2}{|x|+R^2-2|x|R\cos\delta}&=&\frac{1-\rho^2}{\rho^2-2\rho\cos\delta+1}\\
&=&1+2\sum_{n=1}^\infty \rho^n\cos(n\delta),
\end{eqnarray*}
see [16], pp. 18 for an easy proof of this formula, or [4], Vol. II, p. 246.
Contributors and Attributions
Integrated by Justin Marshall.


