18.2: Describing One Network
- Page ID
- 7762
Most social scientists have a reasonable working knowledge of basic univariate and bivariate descriptive and inferential statistics. Many of these tools find immediate application in working with social network data. There are, however, two quite important distinctive features of applying these tools to network data.
First, and most important, social network analysis is about relations among actors, not about relations between variables. Most social scientists have learned their statistics with applications to the study of the distribution of the scores of actors (cases) on variables, and the relations between these distributions. We learn about the mean of a set of scores on the variable "income." We learn about the Pearson zero-order product moment correlation coefficient for indexing linear association between the distribution of actor's incomes and actor's educational attainment.
The application of statistics to social networks is also about describing distributions and relations among distributions. But, rather than describing distributions of attributes of actors (or "variables"), we are concerned with describing the distributions of relations among actors. In applying statistics to network data, we are concerned the issues like the average strength of the relations between actors; we are concerned with questions like "is the strength of ties between actors in a network correlated with the centrality of the actors in the network?" Most of the descriptive statistical tools are the same for attribute analysis and for relational analysis -- but the subject matter is quite different!
Second, many of tools of standard inferential statistics that we learned from the study of the distributions of attributes do not apply directly to network data. Most of the standard formulas for calculating estimated standard errors, computing test statistics, and assessing the probability of null hypotheses that we learned in basic statistics don't work with network data (and, if used, can give us "false positive" answers more often than "false negative"). This is because the "observations" or scores in network data are not "independent" samplings from populations. In attribute analysis, it is often very reasonable to assume that Fred's income and Fred's education are a "trial" that is independent of Sue's income and Sue's education. We can treat Fred and Sue as independent replications.
In network analysis, we focus on relations, not attributes. So, one observation might well be Fred's tie with Sue; another observation might be Fred's tie with George; still another might be Sue's tie with George. These are not "independent" replications. Fred is involved in two observations (as are Sue an George), it is probably not reasonable to suppose that these relations are "independent" because they both involve George.
The standard formulas for computing standard errors and inferential tests on attributes generally assume independent observations. Applying them when the observations are not independent can be very misleading. Instead, alternative numerical approaches to estimating standard errors for network statistics are used. These "boot-strapping" (and permutations) approaches calculate sampling distributions of statistics directly from the observed networks by using random assignment across hundreds or thousands of trials under the assumption that null hypotheses are true.
These general points will become clearer as we examine some real cases. So, let's begin with the simplest univariate descriptive and inferential statistics, and then move on to somewhat more complicated problems.
Univariate Descriptive Statistics
For most of the examples in this chapter, we'll focus again on the Knoke data set that describes the two relations of the exchange of information and the exchange of money among ten organizations operating in the social welfare field. Figure 18.1 lists these data.

Figure 18.1: Listing (Data>Display) of Knoke information and money exchange matrices
These particular data happen to be asymmetric and binary. Most of the statistical tools for working with network data can be applied to symmetric data, and data where the relations are valued (strength, cost, probability of a tie). As with any descriptive statistics, the scale of measurement (binary or valued) does matter in making proper choices about interpretation and application of many statistical tools.
The data that are analyzed with statistical tools when we are working with network data are the observations about relations among actors. So, in each matrix, we have 10 x 10 = 100 observations or cases. For many analyses, the ties of actors with themselves (the main diagonal) are not meaningful, and are not used, so there would be \(\left( N * N - 1 = 90 \right)\) observations. If data are symmetric (i.e. \(X_{ij} = X_{ji}\)), half of these are redundant, and wouldn't be used, so there would be \(\left( N * N - 1 / 2 = 45 \right)\) observations.
What we would like to summarize with our descriptive statistics are some characteristics of the distribution of these scores. Tools>Univariate Stats can be used to generate the most commonly used measures for each matrix (select matrix in the dialog, and chose whether or not to include the diagonal). Figure 18.2 shows the results for our example data, excluding the diagonal.
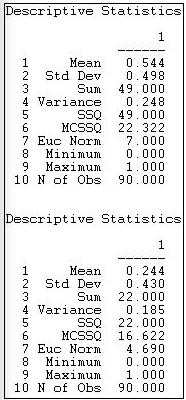
Figure 18.2: Univariate descriptive statistics for Knoke information and money whole networks
For the information sharing relation, we see that we have 90 observations which range from a minimum score of zero to a maximum of one. The sum of the ties is 49, and the average value of the ties is 49/90 = .544. Since the relation has been coded as a "dummy" variable (zero for no relation, one for a relation) the mean is also the proportion of possible ties that are present (or the density), or the probability that any given tie between two random actors is present (54.4% chance).
Several measures of the variability of the distribution are also given. The sums of squared deviations from the mean, variance, and standard deviation are computed -- but are more meaningful for valued than binary data. The Euclidean norm (which is the square root of the sum of squared values) is also provided. One measure not given, but sometimes helpful is the coefficient of variation (standard deviation / mean times 100) equals 91.5. This suggests quite a lot of variation as a percentage of the average score. No statistics on distributional shape (skew or kurtosis) are provided by UCINET.
A quick scan tells us that the mean (or density) for money exchange is lower, and has slightly less variability.
In addition to examining the entire distribution of ties, we might want to examine the distribution of ties for each actor. Since the relation we're looking at is asymmetric or directed, we might further want to summarize each actor's sending (row) and receiving (column). Figures 18.3 and 18.4 show the results of Tools>Univariate Stats for rows (tie sending) and columns (tie receiving) of the information relation matrix.
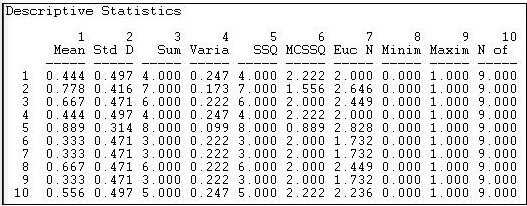
Figure 18.3: Univariate descriptive statistics for Knoke information network rows
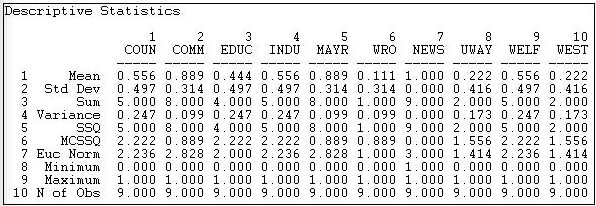
Figure 18.4: Univariate descriptive statistics for Knoke information network columns
We see that actor 1 (COUN) has a mean (or density) of tie sending of 0.444. That is, this actor sent four ties to the available nine other actors. Actor 1 received somewhat more information than they sent, as their column mean is .556. In scanning down the column (in figure 18.3) or row (in figure 18.4) of means, we note that there is quite a bit of variability across actors -- some send more and get more information than others.
With valued data, the means produced index the average strength of ties, rather than the probability of ties. With valued data, measures of variability may be more informative than they are with binary data (since the variability of a binary variable is strictly a function of its mean).
The main point of this brief section is that when we use statistics to describe network data, we are describing properties of the distribution of relations, or ties among actors -- rather than properties of the distribution of attributes across actors. The basic ideas of central tendency and dispersion of distributions apply to the distributions of relational ties in exactly the same way that they do to attribute variables -- but we are describing relations, not attributes.
Hypotheses About One Mean or Density
Of the various properties of the distribution of a single variable (e.g. central tendency, dispersion, skewness), we are usually most interested in central tendency.
If we are working with the distribution of relations among actors in a network, and our measure of tie-strength is binary (zero/one), the mean or central tendency is also the proportion of all ties that are present, and is the "density."
If we are working with the distribution of relations among actors in a network, and our measure of tie-strength is valued, central tendency is usually indicated by the average strength of the tie across all the relations.
We may want to test hypotheses about the density or mean tie strength of a network. In the analysis of variables, this is testing a hypothesis about a single-sample mean or proportion. We might want to be confident that there actually are ties present (null hypothesis: network density is really zero, and any deviation that we observe is due to random variation). We might want to test the hypothesis that the proportion of binary ties present differs from 0.50; we might want to test the hypothesis that the average strength of a valued tie differs from "3."
Network>Compare densities>Against theoretical parameter performs a statistical test to compare the value of a density or average tie strength observed in a network against a test value.
Let's suppose that I think that all organizations have a tendency to want to directly distribute information to all others in their field as a way of legitimating themselves. If this theory is correct, then the density of Knoke's information network should be 1.0. We can see that this isn't true. But, perhaps the difference between what we see (density = 0.544) and what the theory predicts (density = 1.000) is due to random variation (perhaps when we collected the information).
The dialog in figure 18.5 sets up the problem.
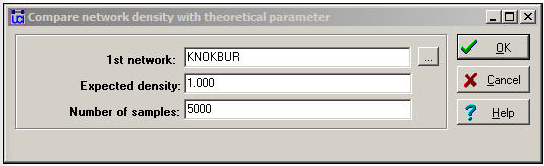
Figure 18.5: Dialog of Compare densities>Against theoretical parameter
The "Expected density" is the value against which we want to test. Here, we are asking the data to convince us that we can be confident in rejecting the idea that organizations send information to all others in their fields.
The parameter "Number of samples" is used for estimating the standard error for the test by the means of "bootstrapping" or computing estimated sampling variance of the mean by drawing 5000 random sub-samples from our network, and constructing a sampling distribution of density measures. The sampling distribution of a statistic is the distribution of the values of that statistic on repeated sampling. The standard deviation of the sampling distribution of a statistic (how much variation we would expect to see from sample to sample just by random chance) is called the standard error. Figure 18.6 shows the results of the hypothesis test

Figure 18.6: Test results
We see that our test value was 1.000, the observed value was 0.5444, so the difference between the null and observed values is -0.4556. How often would a difference this large happen by random sampling variation, if the null hypothesis (density = 1.000) was really true in the population?
Using the classical formula for the standard error of a mean \(\left( s / \sqrt{N} \right)\) we obtain a sampling variability estimate of 0.0528. If we used this for our test, the test statistic would be -0.4556/0.0528 = 8.6 which would be highly significant as a t-test with N-1 degrees of freedom.
However, if we use the bootstrap method of constructing 5000 networks by sampling random sub-sets of nodes each time, and computing the density each time, the mean of this sampling distribution turns out to be 0.4893, and its standard deviation (or the standard error) turns out to be 0.1201.
Using this alternative standard error based on random draws from the observed sample, our test statistic is -3.7943. This test is also significant (p = 0.0002).
Why do this? The classical formula gives an estimate of the standard error (0.0528) that is much smaller than than that created by the bootstrap method (0.1201). This is because the standard formula is based on the notion that all observations (i.e. all relations) are independent. But, since the ties are really generated by the same 10 actors, this is not a reasonable assumption. Using the actual data on the actual actors -- with the observed differences in actor means and variances, is a much more realistic approximation to the actual sampling variability that would occur if, say, we happened to miss Fred when we collected the data on Tuesday.
In general, the standard inferential formulas for computing expected sampling variability (i.e. standard errors) give unrealistically small values for network data. Using them results in the worst kind of inferential error -- the false positive, or rejecting the null when we shouldn't.


