2.3: Binary Numbers
- Page ID
- 9830
Let’s go back to the 1←2 rule and examine what’s really going on.
Whenever there are two dots in single box, they “explode,” disappear, and become one dot in the box to the left.
Two dots in the right-most box is worth one dot in the next box to the left.

If each of the original dots is worth “one,” then the single dot on the left must be worth two.

But we also have two dots in the box of value 2 is worth one dot in the box just to the left...

So that next box must be worth two 2’s, which is four!

And two of these fours make eight.

We said earlier that the 1←2 code for nine dots was 1001. Let’s check:
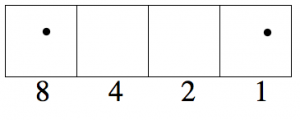
\[8 + 1 = 9 \nonumber \]
so this works!
You should have found that ten dots has 1←2 code 1010.
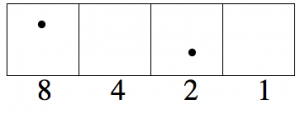
Yep!
\[8 + 2 = 10 \ldotp \nonumber \]
- If there were a box to the left of the 8 box, what would the value of that box be?
- What would be the value of a box two spots to the left of the 8 box? Three spots to the left?
- What number has 1←2 code 100101?
- What is the 1←2 code for two hundred dots?
Numbers written in the 1←2 code are called binary numbers or base two numbers. (The prefix “bi” means “two.”)
From now on, when we want to indicate that a number is written in base two, we will write a subscript “two” on the number.
So \(1001_{two}\) means “the number of dots that has 1←2 code 1001,” which we already saw was nine.
Important! When we read we say “one zero zero one base two.” We don’t say “one thousand and one,” because “thousand” is not a binary number.
- Your first goal: come up with a general method to find the number of dots represented by any binary number. Clearly describe your method. Test your method out on these numbers, and check your work by actually “unexploding” the dots. $$1_{two} \qquad 101_{two} \qquad 1011_{two} \qquad 11111_{two}$$
- Explain why binary numbers only contain the digits 0 and 1.
- Here is a new (harder) goal: come up with a general method to find the binary number related to any number of dots without actually going through the “exploding dot” process. Clearly describe your method. Test your method out on these numbers, and find a way to check your work.
two dots = ___two seventeen dots = ___two
sixty-three dots = ___two one hundred dots = ___two
History
You probably realize by now that a number is an abstract concept with many representations. The standard decimal representation of a number is only one of these. For computers, numbers are always represented in binary. The basic units are transistors which are either on (1) or off (0).

Electronic circuit board from Samsung Galaxy S III.
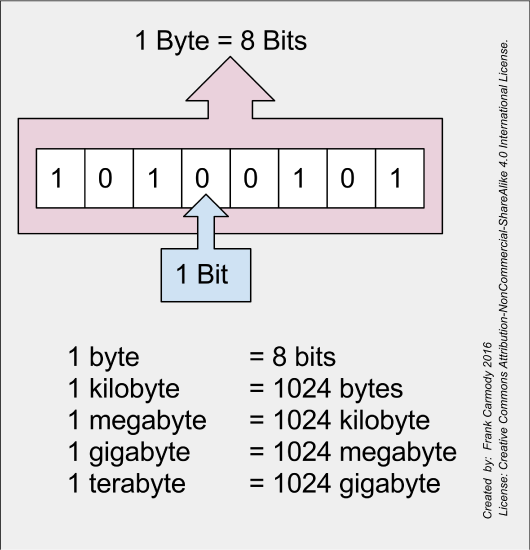
A transistor[1] is said to store one bit of information. Eight bits make a byte and a typical home computer’s central processing unit performs computations on registries that are each 8 bytes (64-bits).
Using the 1←2 rule we can represent the numbers 0 through 18,446,744,073,709,551,615 with 64 bits.
- Image of circuit board from http://www.publicdomainpictures.net/, licensed under CC0 Public Domain. ↵


