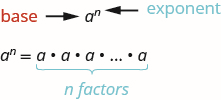2.2: Use the Language of Algebra (Part 2)
- Page ID
- 5779
Simplify Expressions Using the Order of Operations
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values. For example, consider the expression: \[4 + 3 \cdot 7 \nonumber\]
| Some students say it simplifies to | 49 | Some students say it simplifies to | 25 |
| Since 4 + 3 gives 7. | 4 + 3 • 7 = 7 • 7 | Since 3 • 7 is 21. | 4 + 3 • 7 = 4 + 21 |
| And 7 • 7 is 49. | 7 • 7 = 49 | And 21 + 4 makes 25. | 4 + 21 = 25 |
Imagine the confusion that could result if every problem had several different correct answers. The same expression should give the same result. So mathematicians established some guidelines called the order of operations, which outlines the order in which parts of an expression must be simplified.
When simplifying mathematical expressions perform the operations in the following order:
- Parentheses and other Grouping Symbols
- Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
- Exponents
- Simplify all expressions with exponents.
- Multiplication and Division
- Perform all multiplication and division in order from left to right. These operations have equal priority.
- Addition and Subtraction
- Perform all addition and subtraction in order from left to right. These operations have equal priority.
Students often ask, “How will I remember the order?” Here is a way to help you remember: Take the first letter of each key word and substitute the silly phrase. Please Excuse My Dear Aunt Sally.
| Order of Operations | |
|---|---|
| Please | Parentheses |
| Excuse | Exponents |
| My Dear | Multiplication and Division |
| Aunt Sally | Addition and Subtraction |
It’s good that ‘My Dear’ goes together, as this reminds us that multiplication and division have equal priority. We do not always do multiplication before division or always do division before multiplication. We do them in order from left to right.
Similarly, ‘Aunt Sally’ goes together and so reminds us that addition and subtraction also have equal priority and we do them in order from left to right.
Simplify the expressions:
- \(4 + 3 • 7\)
- \((4 + 3) • 7\)
Solution
| Are there any parentheses? No. Are there any exponents? No. Is there any multiplication or division? Yes. | \(4 + 3 \cdot 7\) |
| Multiply first. | \(4 + \textcolor{red}{3 \cdot 7}\) |
| Add. | \(4 + 21\) |
| \(25\) |
| Are there any parentheses? Yes. | \((4 + 3) \cdot 7\) |
| Simplify inside the parentheses. | \(\textcolor{red}{(4 + 3)} \cdot 7\) |
| Are there any exponents? No. Is there any multiplication or division? Yes. | \((7)7\) |
| Multiply. | \(49\) |
Simplify the expressions:
- \(12 − 5 • 2\)
- \((12 − 5) • 2\)
- Answer a
-
\(2\)
- Answer b
-
\(14\)
Simplify the expressions:
- \(8 + 3 • 9\)
- \((8 + 3) • 9\)
- Answer a
-
\(35\)
- Answer b
-
\(99\)
Simplify:
- \(18 ÷ 9 • 2\)
- \(18 • 9 ÷ 2\)
Solution
| Are there any parentheses? No. Are there any exponents? No. Is there any multiplication or division? Yes. | \(18 \div 9 \cdot 2\) |
| Multiply and divide from left to right. Divide. | \(\textcolor{red}{2} \cdot 2\) |
| Multiply. | \(4\) |
| Are there any parentheses? No. Are there any exponents? No. Is there any multiplication or division? Yes. | \(18 \cdot 9 \div 2\) |
| Multiply and divide from left to right. Multiply. | \(\textcolor{red}{162} \div 2\) |
| Divide. | \(81\) |
Simplify: \(42 ÷ 7 • 3\)
- Answer
-
\(18\)
Simplify: \(12 • 3 ÷ 4\)
- Answer
-
\(9\)
Simplify: \(18 ÷ 6 + 4(5 − 2)\).
Solution
| Parentheses? Yes, subtract first. | \(18 \div 6 + 4(5-2)\) |
| Exponents? No. Multiplication or division? Yes. | \(18 \div 6 + 4(\textcolor{red}{3})\) |
| Divide first because we multiply and divide left to right. | \(\textcolor{red}{3} + 4(3)\) |
| Any other multiplication or division? Yes. Multiply. | \(3 + \textcolor{red}{12}\) |
| Any other multiplication or division? No. Any addition or subtraction? Yes | \(15\) |
Simplify: \(30 ÷ 5 + 10(3 − 2)\)
- Answer
-
\(16\)
Simplify: \(70 ÷ 10 + 4(6 − 2)\)
- Answer
-
\(23\)
When there are multiple grouping symbols, we simplify the innermost parentheses first and work outward.
Simplify: \(5 + 2^3 + 3[6 − 3(4 − 2)]\).
Solution
| Are there any parentheses (or other grouping symbol)? Yes. | \(5 + 2^{3} + 3[6-3(4-2)]\) |
| Focus on the parentheses that are inside the brackets. | \(5 + 2^{3} + 3[6-3 \textcolor{red}{(4-2)}]\) |
| Subtract. | \(5 + 2^{3} + 3[6- \textcolor{red}{3(2)}]\) |
| Continue inside the brackets and multiply. | \(5 + 2^{3} + 3[6- \textcolor{red}{6}]\) |
| Continue inside the brackets and subtract. | \(5 + 2^{3} + 3[\textcolor{red}{0}]\) |
| The expression inside the brackets requires no further simplification. | |
| Are there any exponents? Yes. | \(5 + \textcolor{red}{2^{3}} + 3[0]\) |
| Simplify exponents. | \(5 + \textcolor{red}{8} + 3[0]\) |
| Is there any multiplication or division? Yes. | \(5 + 8 + \textcolor{red}{3[0]}\) |
| Multiply. | \(5 + 8 + \textcolor{red}{0}\) |
| Is there any addition or subtraction? Yes. | \(textcolor{red}{5+8+0}\) |
| Add. | \(\textcolor{red}{13} + 0\) |
| Add. | \(13\) |
Simplify: \(9 + 5^3 − [4(9 + 3)]\)
- Answer
-
\(86\)
Simplify: \(7^2 − 2[4(5 + 1)]\)
- Answer
-
\(1\)
Simplify: \(2^3 + 34 ÷ 3 − 5^2\).
Solution
| If an expression has several exponents, they may be simplified in the same step. | \(2^{3} + 3^{4} \div 3 - 5{2}\) |
| Simplify exponents. | \(\textcolor{red}{2^{3}} + \textcolor{red}{3^{4}} \div 3 - \textcolor{red}{5^{2}}\) |
| Divide. | \(8 + \textcolor{red}{81 \div 3} - 25\) |
| Add. | \(\textcolor{red}{8+27} - 25\) |
| Subtract. | \(\textcolor{red}{35-25}\) |
| \(10\) |
Simplify: \(3^2 + 2^4 ÷ 2 + 4^3\)
- Answer
-
\(81\)
Simplify: \(6^2 − 5^3 ÷ 5 + 8^2\)
- Answer
-
\(75\)
Access Additional Online Resources
Key Concepts
| Operation | Notation | Say: | The result is… |
|---|---|---|---|
| Addition | the sum of | ||
| Multiplication | The product of | ||
| Subtraction | the difference of | ||
| Division | \(a\div b, a/b, \dfrac{a}{b}, a \overline{\smash{)}b}\) | The quotient of |
- Equality Symbol
- The symbol \(=\) is called the equal sign.
- Inequality
- \(a>b\) is read \(a\) is greater than \(b\)
| Algebraic Notation | Say |
|---|---|
| is less than or equal to | |
| is greater than or equal to |
- Exponential Notation
- For any expression \(a^n\) is a factor multiplied by itself
- The expression of
Order of Operations When simplifying mathematical expressions perform the operations in the following order:
- Parentheses and other Grouping Symbols: Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
- Exponents: Simplify all expressions with exponents.
- Multiplication and Division: Perform all multiplication and division in order from left to right. These operations have equal priority.
- Addition and Subtraction: Perform all addition and subtraction in order from left to right. These operations have equal priority.
Glossary
- expressions
-
An expression is a number, a variable, or a combination of numbers and variables and operation symbols.
- equation
-
An equation is made up of two expressions connected by an equal sign.
Practice Makes Perfect
Use Variables and Algebraic Symbols
In the following exercises, translate from algebraic notation to words.
- 16 − 9
- 25 − 7
- 5 • 6
- 3 • 9
- 28 ÷ 4
- 45 ÷ 5
- x + 8
- x + 11
- (2)(7)
- (4)(8)
- 14 < 21
- 17 < 35
- 36 ≥ 19
- 42 ≥ 27
- 3n = 24
- 6n = 36
- y − 1 > 6
- y − 4 > 8
- 2 ≤ 18 ÷ 6
- 3 ≤ 20 ÷ 4
- a ≠ 7 • 4
- a ≠ 1 • 12
Identify Expressions and Equations
In the following exercises, determine if each is an expression or an equation.
- 9 • 6 = 54
- 7 • 9 = 63
- 5 • 4 + 3
- 6 • 3 + 5
- x + 7
- x + 9
- y − 5 = 25
- y − 8 = 32
Simplify Expressions with Exponents
In the following exercises, write in exponential form.
- 3 • 3 • 3 • 3 • 3 • 3 • 3
- 4 • 4 • 4 • 4 • 4 • 4
- x • x • x • x • x
- y • y • y • y • y • y
In the following exercises, write in expanded form.
- 53
- 83
- 28
- 105
Simplify Expressions Using the Order of Operations
In the following exercises, simplify.
- (a) 3 + 8 • 5 (b) (3+8) • 5
- (a) 2 + 6 • 3 (b) (2+6) • 3
- 23 − 12 ÷ (9 − 5)
- 32 − 18 ÷ (11 − 5)
- 3 • 8 + 5 • 2
- 4 • 7 + 3 • 5
- 2 + 8(6 + 1)
- 4 + 6(3 + 6)
- 4 • 12 / 8
- 2 • 36 / 6
- 6 + 10 / 2 + 2
- 9 + 12 / 3 + 4
- (6 + 10) ÷ (2 + 2)
- (9 + 12) ÷ (3 + 4)
- 20 ÷ 4 + 6 • 5
- 33 ÷ 3 + 8 • 2
- 20 ÷ (4 + 6) • 5
- 33 ÷ (3 + 8) • 2
- 42 + 52
- 32 + 72
- (4 + 5)2
- (3 + 7)2
- 3(1 + 9 • 6) − 42
- 5(2 + 8 • 4) − 72
- 2[1 + 3(10 − 2)]
- 5[2 + 4(3 − 2)]
Everyday Math
- Basketball In the 2014 NBA playoffs, the San Antonio Spurs beat the Miami Heat. The table below shows the heights of the starters on each team. Use this table to fill in the appropriate symbol (=, <, >).
| Spurs | Height | Heat | Height |
|---|---|---|---|
| Tim Duncan | 83″ | Rashard Lewis | 82" |
| Boris Diaw | 80" | LeBron James | 80" |
| Kawhi Leonard | 79" | Chris Bosh | 83" |
| Tony Parker | 74" | Dwyane Wade | 76" |
| Danny Green | 78" | Ray Allen | 77" |
- Height of Tim Duncan____Height of Rashard Lewis
- Height of Boris Diaw____Height of LeBron James
- Height of Kawhi Leonard____Height of Chris Bosh
- Height of Tony Parker____Height of Dwyane Wade
- Height of Danny Green____Height of Ray Allen
- Elevation In Colorado there are more than 50 mountains with an elevation of over 14,000 feet. The table shows the ten tallest. Use this table to fill in the appropriate inequality symbol.
| Mountain | Elevation |
|---|---|
| Mt. Elbert | 14,433′ |
| Mt. Massive | 14,421′ |
| Mt. Harvard | 14,420′ |
| Blanca Peak | 14,345′ |
| La Plata Peak | 14,336′ |
| Uncompahgre Peak | 14,309′ |
| Crestone Peak | 14,294′ |
| Mt. Lincoln | 14,286′ |
| Grays Peak | 14,270′ |
| Mt. Antero | 14,269′ |
- Elevation of La Plata Peak____Elevation of Mt. Antero
- Elevation of Blanca Peak____Elevation of Mt. Elbert
- Elevation of Gray’s Peak____Elevation of Mt. Lincoln
- Elevation of Mt. Massive____Elevation of Crestone Peak
- Elevation of Mt. Harvard____Elevation of Uncompahgre Peak
Writing Exercises
- Explain the difference between an expression and an equation.
- Why is it important to use the order of operations to simplify an expression?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
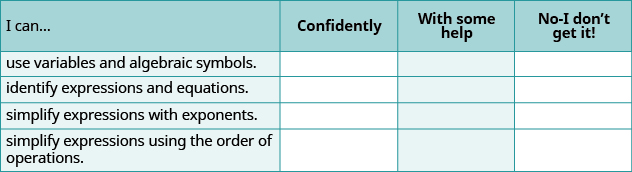
(b) If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.