7.S: The Properties of Real Numbers (Summary)
- Page ID
- 6903
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Key Terms
| Additive Identity | The additive identity is 0. When zero is added to any number, it does not change the value. |
| Additive Inverse | The opposite of a number is its additive inverse. The additive inverse of a is −a . |
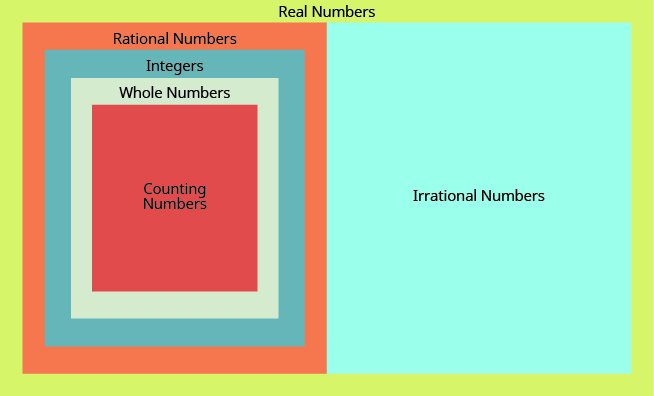
| Irrational number | A number that cannot be written as the ratio of two integers. Its decimal form does not stop and does not repeat. |
| Multiplicative Identity | The multiplicative identity is 1. When one multiplies any number, it does not change the value. |
| Multiplicative Inverse | The reciprocal of a number is its multiplicative inverse. The multiplicative inverse of a is \(\dfrac{1}{a}\). |
| Rational number | A number that can be written in the form \(\dfrac{p}{q}\), where p and q are integers and q ≠ 0. Its decimal form stops or repeats. |
| Real number | A number that is either rational or irrational. |
Key Concepts
7.1 - Rational and Irrational Numbers
- Real numbers
7.2 - Commutative and Associative Properties
- Commutative Properties
- Commutative Property of Addition: If a, b are real numbers, then a + b = b + a
- Commutative Property of Multiplication: If a, b are real numbers, then a • b = b • a
- Associative Properties
- Associative Property of Addition: If a, b, c are real numbers then (a + b) + c = a + (b + c)
- Associative Property of Multiplication: If a, b, c are real numbers then (a • b) • c = a • (b • c)
7.3 - Distributive Property
- Distributive Property:
- If a, b, c are real numbers then
- a(b + c) = ab + ac
- (b + c)a = ba + ca
- a(b - c) = ab - ac
- If a, b, c are real numbers then
7.4 - Properties of Identity, Inverses, and Zero
- Identity Properties
- Identity Property of Addition: For any real number a: a + 0 = a, 0 + a = a
- 0 is the additive identity
- Identity Property of Multiplication: For any real number a: a • 1 = a, 1 • a = a
- 1 is the multiplicative identity
- Identity Property of Addition: For any real number a: a + 0 = a, 0 + a = a
- Inverse Properties
- Inverse Property of Addition: For any real number a: a + (- a) = 0
- - a is the additive inverse of a
- Inverse Property of Multiplication: For any real number a: (a ≠ 0) a • \(\dfrac{1}{a}\) = 1
- \(\dfrac{1}{a}\) is the multiplicative inverse of a
- Inverse Property of Addition: For any real number a: a + (- a) = 0
- Properties of Zero
- Multiplication by Zero: For any real number a, a • 0 = 0, 0 • a = 0
- The product of any number and 0 is 0.
- Division of Zero: For any real number a, \(\frac{0}{a} = 0\), \(0 \div a = 0\)
- Zero divided by any real number, except itself, is zero.
- Division by Zero: For any real number a, \(\dfrac{a}{0}\) is undefined and a ÷ 0 is undefined.
- Division by zero is undefined.
- Multiplication by Zero: For any real number a, a • 0 = 0, 0 • a = 0
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


