2.4: The Derivative Function
- Page ID
- 461
We have seen how to create, or derive, a new function \(f'(x)\) from a function \(f(x)\), and that this new function carries important information. In one example we saw that \(f'(x)\) tells us how steep the graph of \(f(x)\) is; in another we saw that \(f'(x)\) tells us the velocity of an object if \(f(x)\) tells us the position of the object at time \(x\). As we said earlier, this same mathematical idea is useful whenever \(f(x)\) represents some changing quantity and we want to know something about how it changes, or roughly, the "rate'' at which it changes. Most functions encountered in practice are built up from a small collection of "primitive'' functions in a few simple ways, for example, by adding or multiplying functions together to get new, more complicated functions. To make good use of the information provided by \(f'(x)\) we need to be able to compute it for a variety of such functions.
We will begin to use different notations for the derivative of a function. While initially confusing, each is often useful so it is worth maintaining multiple versions of the same thing.
Consider again the function \( f(x)=\sqrt{625-x^2}\). We have computed the derivative \( f'(x)=-x/\sqrt{625-x^2}\), and have already noted that if we use the alternate notation \( y=\sqrt{625-x^2}\) then we might write \( y'=-x/\sqrt{625-x^2}\). Another notation is quite different, and in time it will become clear why it is often a useful one. Recall that to compute the the derivative of \(f\) we computed \( \lim_{\Delta x\to0} {\sqrt{625-(7+\Delta x)^2} - 24\over \Delta x}.\) The denominator here measures a distance in the \(x\) direction, sometimes called the "run'', and the numerator measures a distance in the \(y\) direction, sometimes called the "rise,'' and "rise over run'' is the slope of a line.
Recall that sometimes such a numerator is abbreviated \(\Delta y\), exchanging brevity for a more detailed expression. So in general, a derivative is given by \( y'=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.\) To recall the form of the limit, we sometimes say instead that \( {dy\over dx}=\lim_{\Delta x\to0} {\Delta y\over \Delta x}. \) In other words, \(dy/dx\) is another notation for the derivative, and it reminds us that it is related to an actual slope between two points. This notation is called Leibniz notation, after Gottfried Leibniz, who developed the fundamentals of calculus independently, at about the same time that Isaac Newton did. Again, since we often use \(f\) and \(f(x)\) to mean the original function, we sometimes use \(df/dx\) and \(df(x)/dx\) to refer to the derivative. If the function \(f(x)\) is written out in full we often write the last of these something like this \(f'(x)={d\over dx}\sqrt{625-x^2} \) with the function written to the side, instead of trying to fit it into the numerator.
Example 2.4.1
Find the derivative of \( y=f(t)=t^2\).
Solution
We compute
\[ \eqalign{ y' = \lim_{\Delta t\to0}{\Delta y\over\Delta t}&= \lim_{\Delta t\to0}{(t+\Delta t)^2-t^2\over\Delta t}\cr& =\lim_{\Delta t\to0}{t^2+2t\Delta t+\Delta t^2-t^2\over\Delta t}\cr& =\lim_{\Delta t\to0}{2t\Delta t+\Delta t^2\over\Delta t}\cr& =\lim_{\Delta t\to0} 2t+\Delta t=2t.\cr} \]
Remember that \(\Delta t\) is a single quantity, not a "\(\Delta\)'' times a "\(t\)'', and so \( \Delta t^2\) is \( (\Delta t)^2\) not \( \Delta (t^2)\).
Example 2.4.2
Find the derivative of \(y=f(x)=1/x\).
Solution
The computation:
\[ \eqalign{ y' = \lim_{\Delta x\to0}{\Delta y\over\Delta x}&= \lim_{\Delta x\to0}{ {1\over x+\Delta x} - {1\over x}\over \Delta x}\cr& =\lim_{\Delta x\to0}{ {x\over x(x+\Delta x)} - {x+\Delta x\over x(x+\Delta x)}\over \Delta x}\cr& =\lim_{\Delta x\to0}{ {x-(x+\Delta x)\over x(x+\Delta x)}\over \Delta x}\cr& =\lim_{\Delta x\to0} {x-x-\Delta x\over x(x+\Delta x)\Delta x}\cr& =\lim_{\Delta x\to0} {-\Delta x\over x(x+\Delta x)\Delta x}\cr& =\lim_{\Delta x\to0} {-1\over x(x+\Delta x)}={-1\over x^2}\cr } \]
Note
If you happen to know some "derivative formulas'' from an earlier course, for the time being you should pretend that you do not know them. In examples like the ones above and the exercises below, you are required to know how to find the derivative formula starting from basic principles. We will later develop some formulas so that we do not always need to do such computations, but we will continue to need to know how to do the more involved computations.
Sometimes one encounters a point in the domain of a function \(y=f(x)\) where there is no derivative, because there is no tangent line. In order for the notion of the tangent line at a point to make sense, the curve must be "smooth'' at that point. This means that if you imagine a particle traveling at some steady speed along the curve, then the particle does not experience an abrupt change of direction. There are two types of situations you should be aware of---corners and cusps---where there's a sudden change of direction and hence no derivative.
Example 2.4.3
Discuss the derivative of the absolute value function \(y=f(x)=|x|\).
Solution
If \(x\) is positive, then this is the function \(y=x\), whose derivative is the constant 1. (Recall that when \(y=f(x)=mx+b\), the derivative is the slope \(m\).)
If \(x\) is negative, then we're dealing with the function \(y=-x\), whose derivative is the constant \(-1\).
If \(x=0\), then the function has a corner, i.e., there is no tangent line. A tangent line would have to point in the direction of the curve---but there are two directions of the curve that come together at the origin. We can summarize this as
\[ y'=\cases{ 1& \text{if $x>0$;}\cr -1&\text{if $x < 0$;}\cr \text{undefined}& \text{if $x=0$.}\cr } \]
Example 2.4.4
Discuss the derivative of the function \( y=x^{2/3}\), shown in figure 2.4.1.
Solution
We will later see how to compute this derivative; for now we use the fact that \( y'=(2/3)x^{-1/3}\). Visually this looks much like the absolute value function, but it technically has a cusp, not a corner. The absolute value function has no tangent line at 0 because there are (at least) two obvious contenders---the tangent line of the left side of the curve and the tangent line of the right side. The function \( y=x^{2/3}\) does not have a tangent line at 0, but unlike the absolute value function it can be said to have a single direction: as we approach 0 from either side the tangent line becomes closer and closer to a vertical line; the curve is vertical at 0. But as before, if you imagine traveling along the curve, an abrupt change in direction is required at 0: a full 180 degree turn.
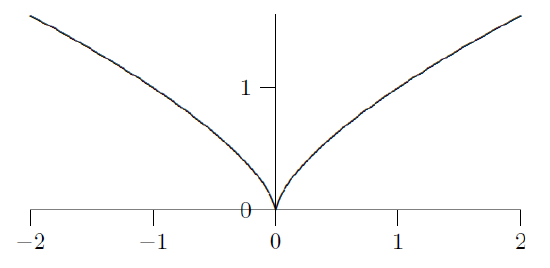
In practice we won't worry much about the distinction between these examples; in both cases the function has a "sharp point'' where there is no tangent line and no derivative.


