1.9: Arc Length
- Page ID
- 2220
Let \(\textbf{r}(t) = (x(t), y(t), z(t))\) be the position vector of an object moving in \(\mathbb{R}^ 3\). Since \(\norm{\textbf{v}(t)}\) is the speed of the object at time \(t\), it seems natural to define the distance \(s\) traveled by the object from time \(t = a \text{ to }t = b\) as the definite integral
\[s = \int_a^b \norm{\textbf{v}(t)}\,dt = \int_a^b \sqrt{ x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2\, dt},\]
which is analogous to the case from single-variable calculus for parametric functions in \(\mathbb{R}^ 2\). This is indeed how we will define the distance traveled and, in general, the arc length of a curve in \(\mathbb{R}^ 3\).
Definition 1.13
Let \(\textbf{f}(t) = (x(t), y(t), z(t))\) be a curve in \(\mathbb{R}^ 3\) whose domain includes the interval \([a,b]\). Suppose that in the interval \((a,b)\) the first derivative of each component function \(x(t), y(t) \text{ and }z(t)\) exists and is continuous, and that no section of the curve is repeated. Then the arc length \(L\) of the curve from \(t = a\) to \(t = b\) is
\[\begin{align} L &= \int_a^b \norm{\textbf{f} ′ (t)}\,dt \\[4pt] &= \int_a^b \sqrt{ x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2 }\,dt \label{Eq1.41} \end{align}\]
A real-valued function whose first derivative is continuous is called continuously differentiable (or a \(C^1\) function), and a function whose derivatives of all orders are continuous is called smooth (or a \(C^∞\) function). All the functions we will consider will be smooth. A smooth curve \(\textbf{f}(t)\) is one whose derivative \(\textbf{f} ′ (t)\) is never the zero vector and whose component functions are all smooth.
Note that we did not prove that the formula in the above definition actually gives the length of a section of a curve. A rigorous proof requires dealing with some subtleties, normally glossed over in calculus texts, which are beyond the scope of this book.
Example 1.41
Find the length \(L\) of the helix \(\textbf{f}(t) = (\cos t,\sin t,t) \text{ from }t = 0 \text{ to }t = 2π\).
Solution
By Equation \ref{Eq1.41}, we have
\[ \begin{align*} L &= \int_0^2π \sqrt{ (−\sin t)^ 2 +(\cos t)^ 2 +1^ 2}\, dt \\[4pt] &= \int_0^2π \sqrt{ \sin^2 t+\cos^2 t+1}\,dt \\[4pt] &= \int_0^2π \sqrt{ 2}\,dt \\[4pt] &=\sqrt{ 2}(2π−0) \\[4pt] &= 2 \sqrt{ 2π} \end{align*}\]
Similar to the case in \(\mathbb{R}^ 2\), if there are values of \(t\) in the interval \([a,b]\) where the derivative of a component function is not continuous then it is often possible to partition \([a,b]\) into subintervals where all the component functions are continuously differentiable (except at the endpoints, which can be ignored). The sum of the arc lengths over the subintervals will be the arc length over \([a,b]\).
Notice that the curve traced out by the function \(\textbf{f}(t) = (\cos t,\sin t,t)\) from Example 1.41 is also traced out by the function \(\textbf{g}(t) = (\cos 2t,\sin 2t,2t)\). For example, over the interval \([0,π],\, \textbf{g}(t)\) traces out the same section of the curve as \(\textbf{f}(t)\) does over the interval \([0,2π]\). Intuitively, this says that \(\textbf{g}(t)\) traces the curve twice as fast as \(\textbf{f}(t)\). This makes sense since, viewing the functions as position vectors and their derivatives as velocity vectors, the speeds of \(\textbf{f}(t) \text{ and }\textbf{g}(t) \text{ are }\norm{\textbf{f} ′ (t)} = \sqrt{ 2} \text{ and }\norm{\textbf{g} ′ (t)} = 2 \sqrt{ 2}\), respectively. We say that \(\textbf{g}(t) \text{ and }\textbf{f}(t)\) are different parametrizations of the same curve.
Definition 1.14
Let \(C\) be a smooth curve in \(\mathbb{R}^ 3\) represented by a function \(\textbf{f}(t)\) defined on an interval \([a,b],\text{ and let }α : [c,d] → [a,b]\) be a smooth one-to-one mapping of an interval \([c,d] \text{ onto }[a,b]\). Then the function \(\textbf{g} : [c,d] → \mathbb{R}^ 3\) defined by \(\textbf{g}(s) = \textbf{f}(α(s))\) is a parametrization of \(C\) with parameter \(s\). If \(α\) is strictly increasing on \([c,d]\) then we say that \(\textbf{g}(s)\) is equivalent to \(\textbf{f}(t)\).
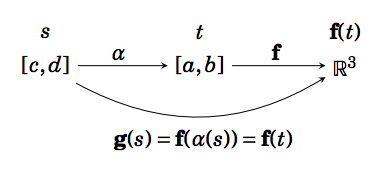
Note that the differentiability of \(\textbf{g}(s)\) follows from a version of the Chain Rule for vector-valued functions (the proof is left as an exercise):
Theorem 1.21 Chain Rule:
If \(\textbf{f}(t)\) is a differentiable vector-valued function of \(t\), and \(t = α(s)\) is a differentiable scalar function of \(s\), then \(\textbf{f}(s) = \textbf{f}(α(s))\) is a differentiable vector-valued function of \(s\), and
\[\dfrac{d\textbf{f}}{ ds} = \dfrac{d\textbf{f}}{ dt} \dfrac{dt}{ ds}\]
for any \(s\) where the composite function \(\textbf{f}(α(s))\) is defined.
Example 1.42
The following are all equivalent parametrizations of the same curve:
\[ \begin{align} \textbf{f}(t) &= (\cos t,\sin t,t) \text{ for }t \text{ in }[0,2π] \\[4pt] \nonumber \textbf{g}(s) &= (\cos 2s,\sin 2s,2s) \text{ for }s \text{ in }[0,π] \\[4pt] \nonumber \textbf{h}(s) &= (\cos 2πs,\sin 2πs,2πs) \text{ for }s \text{ in }[0,1] \end{align}\]
To see that \(\textbf{g}(s)\) is equivalent to \(\textbf{f}(t)\), define \(α : [0,π] → [0,2π] \text{ by }α(s) = 2s\). Then \(α\) is smooth, one-to-one, maps \([0,π]\) onto \([0,2π]\), and is strictly increasing (since \(α ′ (s) = 2 > 0 \text{ for all } s\)). Likewise, defining \(α : [0,1] → [0,2π] \text{ by }α(s) = 2πs\) shows that \(\textbf{h}(s)\) is equivalent to \(\textbf{f}(t)\).
A curve can have many parametrizations, with different speeds, so which one is the best to use? In some situations the arc length parametrization can be useful. The idea behind this is to replace the parameter \(t\), for any given smooth parametrization \(\textbf{f}(t) \text{ defined on }[a,b]\), by the parameter \(s\) given by
\[\label{Eq1.43} s = s(t) = \int_a^t \norm{\textbf{f} ′ (u)}\,du.\]
In terms of motion along a curve, \(s\) is the distance traveled along the curve after time \(t\) has elapsed. So the new parameter will be distance instead of time. There is a natural correspondence between \(s \text{ and }t\): from a starting point on the curve, the distance traveled along the curve (in one direction) is uniquely determined by the amount of time elapsed, and vice versa.
Since \(s\) is the arc length of the curve over the interval \([a,t]\) for each \(t\) in \([a,b]\), then it is a function of \(t\). By the Fundamental Theorem of Calculus, its derivative is
\[\begin{align*} s ′ (t) &= \dfrac{ds}{ dt} \\[4pt] &= \dfrac{d}{ dt} \int_a^t \norm{\textbf{f} ′ (u)}\,du \\[4pt] &= \norm{\textbf{f} ′ (t)}\text{ for all }t \text{ in }[a,b]. \end{align*}\]
Since \(\textbf{f}(t)\) is smooth, then \(\norm{\textbf{f} ′ (t)} > 0\) for all \(t \text{ in }[a,b]\). Thus \(s ′ (t) > 0\) and hence \(s(t)\) is strictly increasing on the interval \([a,b]\). Recall that this means that \(s\) is a one-to-one mapping of the interval \([a,b]\) onto the interval \([s(a),\, s(b)]\). But we see that
\[\begin{align*} s(a) &= \int_a^a \norm{\textbf{f} ′ (u)}\,du \\[4pt] &= 0 \text{ and }s(b) \\[4pt] &= \int_a^b \norm{\textbf{f} ′ (u)}\,du \\[4pt] &= L \\[4pt] &= \text{ arc length from }t = a \text{ to }t = b \end{align*}\]
So the function \(s : [a,b] → [0,L]\) is a one-to-one, differentiable mapping onto the interval \([0,L]\). From single-variable calculus, we know that this means that there exists an inverse function \(α : [0,L] → [a,b]\) that is differentiable and the inverse of \(s : [a,b] → [0,L]\). That is, for each \(t\) in \([a,b]\) there is a unique \(s\) in \([0,L]\) such that \(s = s(t)\text{ and }t = α(s)\). And we know that the derivative of \(α\) is
\[\nonumber α ′ (s) = \dfrac{1}{ s ′ (α(s))} = \dfrac{1}{\norm{\textbf{f} ′ (α(s))}}\]
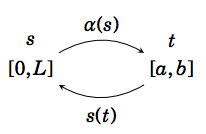
So define the arc length parametrization \(\textbf{f}: [0,L] → \mathbb{R}^ 3\) by
\[\nonumber \textbf{f}(s) = \textbf{f}(α(s))\text{ for all }s\text{ in }[0,L].\]
Then \(\textbf{f}(s)\) is smooth, by the Chain Rule. In fact, \(\textbf{f}(s)\) has unit speed:
\[\nonumber \begin{align} \textbf{f} ′ (s) &= \textbf{f} ′ (α(s))α ′ (s) \text{ by the Chain Rule, so} \\[4pt] \nonumber &=\textbf{f} ′ (α(s)) \dfrac{1}{ \norm{\textbf{f} ′ (α(s))}} ,\text{ so} \\[4pt] \nonumber \norm{\textbf{f} ′ (s)} &= 1 \text{ for all }s \text{ in }[0,L]. \\[4pt] \end{align}\]
So the arc length parametrization traverses the curve at a “normal” rate.
In practice, parametrizing a curve \(\textbf{f}(t)\) by arc length requires you to evaluate the integral \(s = \int_a^t \norm{\textbf{f} ′ (u)}\,du\) in some closed form (as a function of \(t\)) so that you could then solve for \(t\) in terms of \(s\). If that can be done, you would then substitute the expression for \(t \text{ in terms of }s\) (which we called \(α(s)\)) into the formula for \(\textbf{f}(t) \text{ to get }\textbf{f}(s)\).
Example 1.43
Parametrize the helix \(\textbf{f}(t) = (\cos t,\sin t,t), \text{ for }\text{ in }[0,2π]\), by arc length.
Solution
By Example 1.41 and Equation \ref{Eq1.43}, we have
\[\nonumber s = \int_0^t \norm{\textbf{f} ′ (u)}\,du = \int_0^t \sqrt{ 2}\,du = \sqrt{ 2} t \text{ for all \(t\) in }[0,2π].\]
So we can solve for \(t\) in terms of \(s:\, t = α(s) = \dfrac{s}{ \sqrt{ 2}}\).
\(∴ \textbf{f}(s) = \left ( \cos \dfrac{s}{ \sqrt{ 2}} ,\sin \dfrac{s}{ \sqrt{ 2}} , \dfrac{s}{ \sqrt{ 2}} \right ) \) for all \(s\) in \([0,2 p 2π]\). Note that \(\norm{\textbf{f} ′ (s)} = 1\).
Arc length plays an important role when discussing curvature and moving frame fields, in the field of mathematics known as differential geometry. The methods involve using an arc length parametrization, which often leads to an integral that is either difficult or impossible to evaluate in a simple closed form. The simple integral in Example 1.43 is the exception, not the norm. In general, arc length parametrizations are more useful for theoretical purposes than for practical computations. Curvature and moving frame fields can be defined without using arc length, which makes their computation much easier, and these definitions can be shown to be equivalent to those using arc length. We will leave this to the exercises.
The arc length for curves given in other coordinate systems can also be calculated:
Theorem 1.22: Arc length in Cylindrical coordinates
Suppose that \(r = r(t),\, θ = θ(t) \text{ and }z = z(t)\) are the cylindrical coordinates of a curve \(\textbf{f}(t), \text{ for \(t\) in }[a,b]\). Then the arc length \(L\) of the curve over \([a,b]\) is
\[\label{Eq1.44} L = \int_a^b \sqrt{ r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 + z ′ (t)^ 2}\, dt\]
Proof
The Cartesian coordinates \((x(t), y(t), z(t))\) of a point on the curve are given by
\[\nonumber x(t) = r(t)\cos θ(t),\quad y(t) = r(t)\sin θ(t),\quad z(t) = z(t)\]
so differentiating the above expressions for \(x(t) \text{ and }y(t)\) with respect to \(t\) gives
\[\nonumber x ′ (t) = r ′ (t)\cos θ(t)− r(t)θ ′ (t)\sin θ(t),\quad y ′ (t) = r ′ (t)\sin θ(t)+ r(t)θ ′ (t)\cos θ(t) \]
and so
\[\nonumber \begin{align} x ′ (t)^ 2 + y ′ (t)^ 2 &= (r ′ (t)\cos θ(t)− r(t)θ ′ (t)\sin θ(t))^2 +(r ′ (t)\sin θ(t)+ r(t)θ ′ (t)\cos θ(t))^2 \\[4pt] \nonumber &=r ′ (t)^ 2 (\cos^2 θ +\sin^2 θ)+ r(t)^ 2 θ ′ (t)^ 2 (\cos^2 θ +\sin^2 θ) \\[4pt] \nonumber \quad &-2r ′ (t)r(t)θ ′ (t)\cos θ \sin θ +2r ′ (t)r(t)θ ′ (t)\cos θ \sin θ \\[4pt] \nonumber &= r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 ,\text{ and so} \\[4pt] \nonumber L&= \int_a^b \sqrt{ x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2}\, dt \\[4pt] \nonumber &=\int_a^b \sqrt{ r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 + z ′ (t)^ 2}\, dt \\[4pt] \end{align}\]
\(\textbf{QED}\)
Example 1.44
Find the arc length \(L\) of the curve whose cylindrical coordinates are \(r = e^ t , θ = t \text{ and }z = e^ t\), for \(t\) over the interval \([0,1]\).
Solution
Since \(r ′ (t) = e^ t ,\, θ ′ (t) = 1 \text{ and }z ′ (t) = e^ t\), then
\[\nonumber \begin{align} L &= \int_0^1 \sqrt{ r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 + z ′ (t)^ 2}\, dt \\[4pt] \nonumber &=\int_0^1 \sqrt{ e^ {2t} + e^ {2t} (1)+ e^ {2t}}\, dt \\[4pt] \nonumber &=\int_0^1 e^ t \sqrt{ 3}\,dt = \sqrt{ 3}(e −1) \\[4pt] \end{align}\]


