1.6: Surfaces
- Page ID
- 2217
In the previous section we discussed planes in Euclidean space. A plane is an example of a \(\textit{surface}\), which we will define informally as the solution set of the equation \(F(x,y,z) = 0\) in \(\mathbb{R}^{3}\), for some real-valued function \(F\). For example, a plane given by \(ax + by + cz + d = 0\) is the solution set of \(F(x,y,z) = 0\) for the function \(F(x,y,z) = ax + by + cz + d\). Surfaces are 2-dimensional. The plane is the simplest surface, since it is "flat''. In this section we will look at some surfaces that are more complex, the most important of which are the sphere and the cylinder.
Definition: Sphere
A \(\textbf{sphere}\) \(S\) is the set of all points \((x,y,z)\) in \(\mathbb{R}^{3}\) which are a fixed distance \(r\) (called the \(\textbf{radius}\)) from a fixed point \(P_{0} = (x_{0}, y_{0}, z_{0})\) (called the \(\textbf{center}\) of the sphere):
\[S = \lbrace \, (x,y,z): \, (x - x_{0})^{2} + (y - y_{0})^{2} + (z - z_{0})^{2} = r^{2} \, \rbrace \label{Eq1.29}\]
Using vector notation, this can be written in the equivalent form:
\[S = \lbrace \, \textbf{x}: \, \norm{\textbf{x} - \textbf{x}_{0}} = r \, \rbrace\]
where \(\textbf{x} = (x,y,z)\) and \(\textbf{x}_{0} = (x_{0}, y_{0}, z_{0})\) are vectors.
Figure \(\PageIndex{1}\) illustrates the vectorial approach to spheres.
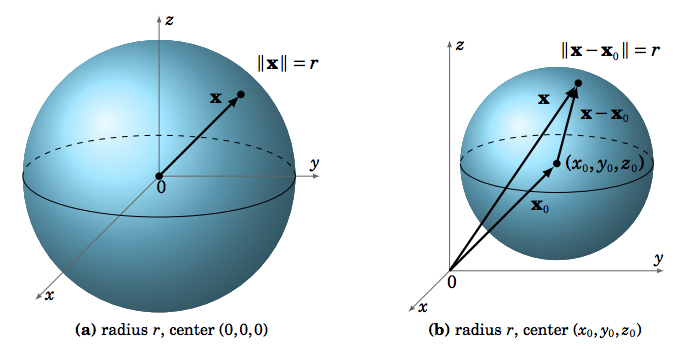
Note in Figure \(\PageIndex{1a}\) that the intersection of the sphere with the \(xy\)-plane is a circle of radius \(r\) (i.e. a \(\textit{great circle}\), given by \(x^{2} + y^{2} = r^{2}\) as a subset of \(\mathbb{R}^{2}\)). Similarly for the intersections with the \(xz\)-plane and the \(yz\)-plane. In general, a plane intersects a sphere either at a single point or in a circle.
Example \(\PageIndex{1}\): Intersection of a sphere and a plane
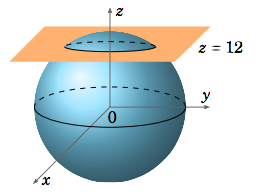
Find the intersection of the sphere \(x^{2} + y^{2} + z^{2} = 169\) with the plane \(z = 12\).
The sphere is centered at the origin and has radius \(13 = \sqrt{169}\), so it does intersect the plane \(z = 12\). Putting \(z = 12\) into the equation of the sphere gives
\[\begin{align*} \nonumber x^{2} + y^{2} + 12^{2} &= 169 \\[4pt] \nonumber x^{2} + y^{2} &= 169 - 144 = 25 = 5^{2} \end{align*}\]
which is a circle of radius \(5\) centered at \((0,0,12)\), parallel to the \(xy\)-plane (Figure \(\PageIndex{2}\)).
If the equation in Equation \ref{Eq1.29} is multiplied out, we get an equation of the form:
\[x^{2} + y^{2} + z^{2} + ax + by + cz + d = 0\]
for some constants \(a\), \(b\), \(c\) and \(d\). Conversely, an equation of this form \(\textit{may}\) describe a sphere, which can be determined by completing the square for the \(x\), \(y\) and \(z\) variables.
Example \(\PageIndex{2}\)
Is \(2x^{2} + 2y^{2} + 2z^{2} - 8x + 4y - 16z + 10 = 0\) the equation of a sphere?
Solution
Dividing both sides of the equation by \(2\) gives
\[\nonumber x^{2} + y^{2} + z^{2} - 4x + 2y - 8z + 5 = 0\]
\[\nonumber (x^{2} - 4x + 4) + (y^{2} + 2y + 1) + (z^{2} - 8z + 16) + 5 - 4 - 1 - 16 = 0\]
\[\nonumber (x - 2)^{2} + (y + 1)^{2} + (z - 4)^{2} = 16\]
which is a sphere of radius \(4\) centered at \((2,-1,4)\).
Example \(\PageIndex{3}\)
Find the points(s) of intersection (if any) of the sphere from Example \(\PageIndex{2}\) and the line \(x = 3 + t\), \(y = 1 + 2t\), \(z = 3 - t\).
Solution
Put the equations of the line into the equation of the sphere, which was \((x - 2)^{2} + (y + 1)^{2} + (z - 4)^{2} = 16\), and solve for \(t\):
\begin{align*}
\nonumber (3 + t - 2)^{2} + (1 + 2t + 1)^{2} + (3 - t - 4)^{2} &= 16\\[4pt]
\nonumber (t + 1)^{2} + (2t + 2)^{2} + (-t - 1)^{2} &= 16\\[4pt]
\nonumber 6t^{2} + 12t -10 &= 0
\end{align*}
The quadratic formula gives the solutions \(~t = -1 \pm \dfrac{4}{\sqrt{6}}\). Putting those two values into the equations of the line gives the following two points of intersection:
\[\nonumber \left( 2 + \frac{4}{\sqrt{6}}, -1 + \frac{8}{\sqrt{6}}, 4 - \frac{4}{\sqrt{6}} \right) \text{ and } \left( 2 - \frac{4}{\sqrt{6}}, -1 - \frac{8}{\sqrt{6}}, 4 + \frac{4}{\sqrt{6}} \right)\]
If two spheres intersect, they do so either at a single point or in a circle (unless they are identical size and not displaced from each other).
Example \(\PageIndex{4}\)
Find the intersection (if any) of the spheres \(x^{2} + y^{2} + z^{2} = 25\) and \(x^{2} + y^{2} + (z - 2)^{2} = 16\).
Solution
For any point \((x,y,z)\) on both spheres, we see that
\begin{align*}
\nonumber x^{2} + y^{2} + z^{2} = 25 &\Rightarrow x^{2} + y^{2} = 25 - z^{2}, \text{and}\\[4pt]
\nonumber x^{2} + y^{2} + (z - 2)^{2} = 16 &\Rightarrow x^{2} + y^{2} = 16 - (z - 2)^{2}, \text{so}\\[4pt]
\nonumber 16 - (z - 2)^{2} = 25 - z^{2} &\Rightarrow 4z - 4 = 9 \Rightarrow z = 13/4\\[4pt]
\nonumber &\Rightarrow x^{2} + y^{2} = 25 - (13/4)^{2} = 231/16
\end{align*}
\(\therefore\) The intersection is the circle \(x^{2} + y^{2} = \frac{231}{16}\) of radius \(\frac{\sqrt{231}}{4} \approx 3.8\) centered at \((0,0,\frac{13}{4})\).
The cylinders that we will consider are \(\textit{right circular cylinders}\). These are cylinders obtained by moving a line \(L\) along a circle \(C\) in \(\mathbb{R}^{3}\) in a way so that \(L\) is always perpendicular to the plane containing \(C\). We will only consider the cases where the plane containing \(C\) is parallel to one of the three coordinate planes (Figure \(\PageIndex{3}\)).
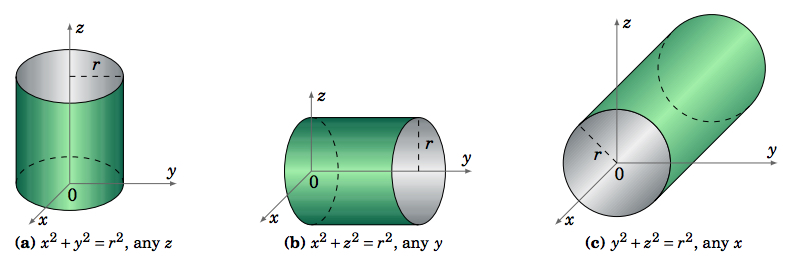
For example, the equation of a cylinder whose base circle \(C\) lies in the \(xy\)-plane and is centered at \((a,b,0)\) and has radius \(r\) is
\begin{equation}\label{eqn:cylxy}
(x - a)^2 + (y - b)^2 = r^2,
\end{equation}
where the value of the \(z\) coordinate is unrestricted. Similar equations can be written when the base circle lies in one of the other coordinate planes. A plane intersects a right circular cylinder in a circle, ellipse, or one or two lines, depending on whether that plane is parallel, oblique, or perpendicular, respectively, to the plane containing \(C\). The intersection of a surface with a plane is called the \(\textbf{trace}\) of the surface.
The equations of spheres and cylinders are examples of second-degree equations in \(\mathbb{R}^ 3\), i.e. equations of the form
\begin{equation}\label{Eq1.33}
Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0
\end{equation}
for some constants \(A, B, \dots, J\). If the above equation is not that of a sphere, cylinder, plane, line or point, then the resulting surface is called a quadric surface.
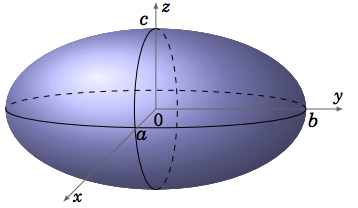
One type of quadric surface is the \(\textbf{ellipsoid}\), given by an equation of the form:
\begin{equation}\label{eqn:ellipsoid}
\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1
\end{equation}
In the case where \(a = b = c\), this is just a sphere. In general, an ellipsoid is egg-shaped (think of an ellipse rotated around its major axis). Its traces in the coordinate planes are ellipses.
Two other types of quadric surfaces are the \(\textbf{hyperboloid of one sheet}\), given by an equation of the form:
\begin{equation}\label{eqn:hyperboloidone}
\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1
\end{equation}
and the \(\textbf{hyperboloid of two sheets}\), whose equation has the form:
\begin{equation}\label{eqn:hyperboloidtwo}
\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1
\end{equation}
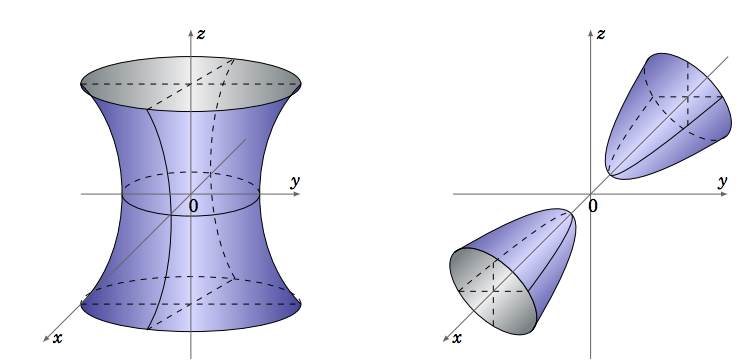
For the hyperboloid of one sheet, the trace in any plane parallel to the \(xy\)-plane is an ellipse. The traces in the planes parallel to the \(xz\)- or \(yz\)-planes are hyperbolas (Figure \(\PageIndex{5}\)), except for the special cases \(x = \pm a\) and \(y = \pm b\); in those planes the traces are pairs of intersecting lines (see Exercise 8).
For the hyperboloid of two sheets, the trace in any plane parallel to the \(xy\)- or \(xz\)-plane is a hyperbola (Figure \(\PageIndex{6}\)). There is no trace in the \(yz\)-plane. In any plane parallel to the \(yz\)-plane for which \(\lvert x \rvert > \lvert a \rvert \), the trace is an ellipse.
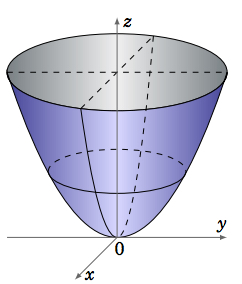
The \(\textbf{elliptic paraboloid}\) is another type of quadric surface, whose equation has the form:
\begin{equation}\label{eqn:paraboloid}
\frac{x^2}{a^2} + \frac{y^2}{b^2} = \frac{z}{c}
\end{equation}
The traces in planes parallel to the \(xy\)-plane are ellipses, though in the \(xy\)-plane itself the trace is a single point. The traces in planes parallel to the \(xz\)- or \(yz\)-planes are parabolas. Figure \(\PageIndex{7}\) shows the case where \(c > 0\). When \(c < 0\) the surface is turned downward. In the case where \(a = b\), the surface is called a paraboloid of revolution, which is often used as a reflecting surface, e.g. in vehicle headlights.
A more complicated quadric surface is the \(\textbf{hyperbolic paraboloid}\), given by:
\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = \dfrac{z}{c}\label{Eq1.38}\]
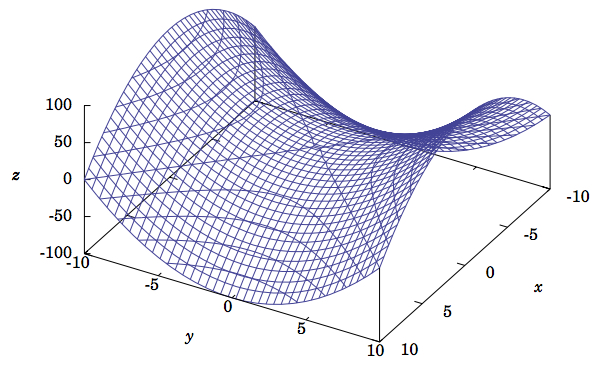
The hyperbolic paraboloid can be tricky to draw; using graphing software on a computer can make it easier. For example, Figure \(\PageIndex{8}\) was created using the free Gnuplot package (see Appendix C). It shows the graph of the hyperbolic paraboloid \(z = y^2 - x^2\), which is the special case where \(a = b = 1\) and \(c = -1\) in Equation \ref{Eq1.38}. The mesh lines on the surface are the traces in planes parallel to the coordinate planes. So we see that the traces in planes parallel to the \(xz\)-plane are parabolas pointing upward, while the traces in planes parallel to the \(yz\)-plane are parabolas pointing downward. Also, notice that the traces in planes parallel to the \(xy\)-plane are hyperbolas, though in the \(xy\)-plane itself the trace is a pair of intersecting lines through the origin. This is true in general when \(c < 0\) in Equation \ref{Eq1.38}. When \(c > 0\), the surface would be similar to that in Figure \(\PageIndex{8}\), only rotated \(90^\circ \) around the \(z\)-axis and the nature of the traces in planes parallel to the \(xz\)- or \(yz\)-planes would be reversed.
The last type of quadric surface that we will consider is the \(\textbf{elliptic cone}\), which has an equation of the form:
\begin{equation}\label{eqn:ellipcone}
\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0
\end{equation}
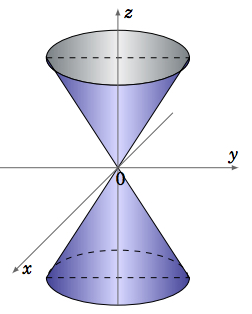
The traces in planes parallel to the \(xy\)-plane are ellipses, except in the \(xy\)-plane itself where the trace is a single point. The traces in planes parallel to the \(xz\)- or \(yz\)-planes are hyperbolas, except in the \(xz\)- and \(yz\)-planes themselves where the traces are pairs of intersecting lines.
Ruled Surface
Notice that every point on the elliptic cone is on a line which lies entirely on the surface; in Figure \(\PageIndex{9}\) these lines all go through the origin. This makes the elliptic cone an example of a ruled surface. The cylinder is also a ruled surface.
What may not be as obvious is that both the hyperboloid of one sheet and the hyperbolic paraboloid are ruled surfaces. In fact, on both surfaces there are two lines through each point on the surface (Exercises 11-12). Such surfaces are called doubly ruled surfaces, and the pairs of lines are called a regulus.
It is clear that for each of the six types of quadric surfaces that we discussed, the surface can be translated away from the origin (e.g. by replacing \(x^2\) by \((x - x_0)^2\) in its equation). It can be proved that every quadric surface can be translated and/or rotated so that its equation matches one of the six types that we described. For example, \(z = 2xy\) is a case of Equation \ref{Eq1.33} with "mixed'' variables, e.g. with \(D \ne 0\) so that we get an \(xy\) term. This equation does not match any of the types we considered. However, by rotating the \(x\)-and \(y\)-axes by \(45^\circ\) in the \(xy\)-plane by means of the coordinate transformation \(x = (x' - y')/\sqrt{2}\), \(y = (x' + y')/\sqrt{2}\), \(z = z'\), then \(z = 2xy\) becomes the hyperbolic paraboloid \(z' = (x')^2 - (y')^2\) in the \((x',y',z')\) coordinate system. That is, \(z = 2xy\) is a hyperbolic paraboloid as in Equation \ref{Eq1.38}, but rotated \(45^\circ \) in the \(xy\)-plane.


