4.4: The Mean Value Theorem
- Page ID
- 2503
Learning Objectives
- Explain the meaning of Rolle’s theorem.
- Describe the significance of the Mean Value Theorem.
- State three important consequences of the Mean Value Theorem.
The Mean Value Theorem is one of the most important theorems in calculus. We look at some of its implications at the end of this section. First, let’s start with a special case of the Mean Value Theorem, called Rolle’s theorem.
Rolle’s Theorem
Informally, Rolle’s theorem states that if the outputs of a differentiable function \(f\) are equal at the endpoints of an interval, then there must be an interior point \(c\) where \(f'(c)=0\). Figure \(\PageIndex{1}\) illustrates this theorem.
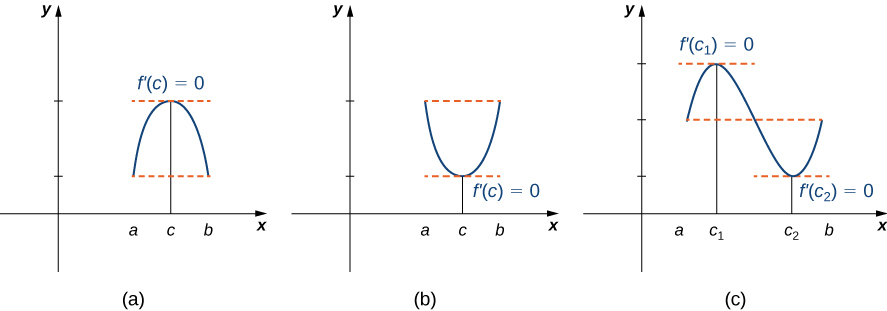
Rolle’s Theorem
Let \(f\) be a continuous function over the closed interval \([a,b]\) and differentiable over the open interval \((a,b)\) such that \(f(a)=f(b)\). There then exists at least one \(c∈(a,b)\) such that \(f'(c)=0.\)
Proof
Let \(k=f(a)=f(b).\) We consider three cases:
- \(f(x)=k\) for all \(x∈(a,b).\)
- There exists \(x∈(a,b)\) such that \(f(x)>k.\)
- There exists \(x∈(a,b)\) such that \(f(x)<k.\)
Case 1: If \(f(x)=k\) for all \(x∈(a,b)\), then \(f'(x)=0\) for all \(x∈(a,b).\)
Case 2: Since \(f\) is a continuous function over the closed, bounded interval \([a,b]\), by the extreme value theorem, it has an absolute maximum. Also, since there is a point \(x∈(a,b)\) such that \(f(x)>k\), the absolute maximum is greater than \(k\). Therefore, the absolute maximum does not occur at either endpoint. As a result, the absolute maximum must occur at an interior point \(c∈(a,b)\). Because \(f\) has a maximum at an interior point \(c\), and \(f\) is differentiable at \(c\), by Fermat’s theorem, \(f'(c)=0.\)
Case 3: The case when there exists a point \(x∈(a,b)\) such that \(f(x)<k\) is analogous to case 2, with maximum replaced by minimum.
□
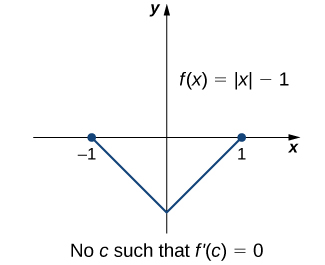
An important point about Rolle’s theorem is that the differentiability of the function \(f\) is critical. If \(f\) is not differentiable, even at a single point, the result may not hold. For example, the function \(f(x)=|x|−1\) is continuous over \([−1,1]\) and \(f(−1)=0=f(1)\), but \(f'(c)≠0\) for any \(c∈(−1,1)\) as shown in the following figure.
Let’s now consider functions that satisfy the conditions of Rolle’s theorem and calculate explicitly the points \(c\) where \(f'(c)=0.\)
Example \(\PageIndex{1}\): Using Rolle’s Theorem
For each of the following functions, verify that the function satisfies the criteria stated in Rolle’s theorem and find all values \(c\) in the given interval where \(f'(c)=0.\)
- \(f(x)=x^2+2x\) over \([−2,0]\)
- \(f(x)=x^3−4x\) over \([−2,2]\)
Solution
a. Since \(f\) is a polynomial, it is continuous and differentiable everywhere. In addition, \(f(−2)=0=f(0).\) Therefore, \(f\) satisfies the criteria of Rolle’s theorem. We conclude that there exists at least one value \(c∈(−2,0)\) such that \(f'(c)=0\). Since \(f'(x)=2x+2=2(x+1),\) we see that \(f'(c)=2(c+1)=0\) implies \(c=−1\) as shown in the following graph.

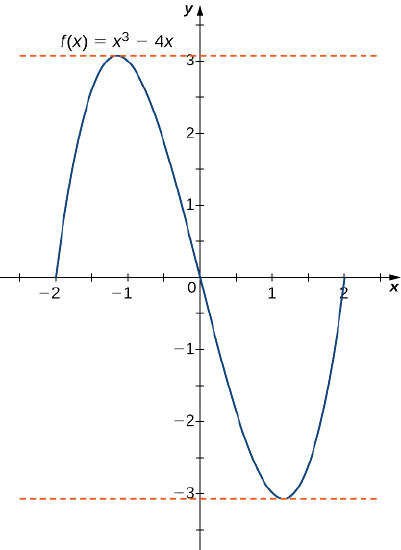
b. As in part a. \(f\) is a polynomial and therefore is continuous and differentiable everywhere. Also, \(f(−2)=0=f(2).\) That said, \(f\) satisfies the criteria of Rolle’s theorem. Differentiating, we find that \(f'(x)=3x^2−4.\) Therefore, \(f'(c)=0\) when \(x=±\frac{2}{\sqrt{3}}\). Both points are in the interval \([−2,2]\), and, therefore, both points satisfy the conclusion of Rolle’s theorem as shown in the following graph.
Exercise \(\PageIndex{1}\)
Verify that the function \(f(x)=2x^2−8x+6\) defined over the interval \([1,3]\) satisfies the conditions of Rolle’s theorem. Find all points \(c\) guaranteed by Rolle’s theorem.
- Hint
-
Find all values \(c\), where \(f'(c)=0\).
- Answer
-
\(c=2\)
The Mean Value Theorem and Its Meaning
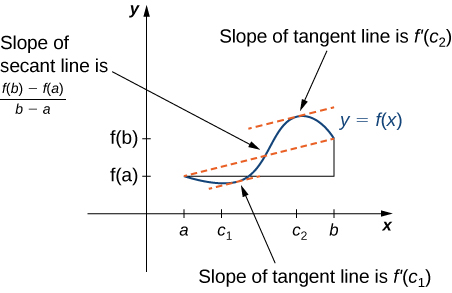
Rolle’s theorem is a special case of the Mean Value Theorem. In Rolle’s theorem, we consider differentiable functions \(f\) that are zero at the endpoints. The Mean Value Theorem generalizes Rolle’s theorem by considering functions that are not necessarily zero at the endpoints. Consequently, we can view the Mean Value Theorem as a slanted version of Rolle’s theorem (Figure \(\PageIndex{5}\)). The Mean Value Theorem states that if \(f\) is continuous over the closed interval \([a,b]\) and differentiable over the open interval \((a,b)\), then there exists a point \(c∈(a,b)\) such that the tangent line to the graph of \(f\) at \(c\) is parallel to the secant line connecting \((a,f(a))\) and \((b,f(b)).\)
Mean Value Theorem
Let \(f\) be continuous over the closed interval \([a,b]\) and differentiable over the open interval \((a,b)\). Then, there exists at least one point \(c∈(a,b)\) such that
\[f'(c)=\frac{f(b)−f(a)}{b−a} \nonumber \]
Proof
The proof follows from Rolle’s theorem by introducing an appropriate function that satisfies the criteria of Rolle’s theorem. Consider the line connecting \((a,f(a))\) and \((b,f(b)).\) Since the slope of that line is
\[\frac{f(b)−f(a)}{b−a} \nonumber \]
and the line passes through the point \((a,f(a)),\) the equation of that line can be written as
\[y=\frac{f(b)−f(a)}{b−a}(x−a)+f(a). \nonumber \]
Let \(g(x)\) denote the vertical difference between the point \((x,f(x))\) and the point \((x,y)\) on that line. Therefore,
\[g(x)=f(x)−\left[\frac{f(b)−f(a)}{b−a}(x−a)+f(a)\right]. \nonumber \]
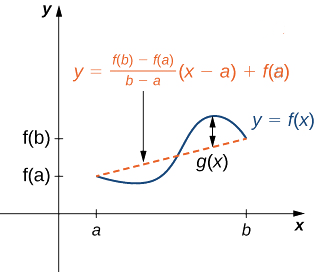 Figure \(\PageIndex{6}\): The value \(g(x)\) is the vertical difference between the point \((x,f(x))\) and the point \((x,y)\) on the secant line connecting \((a,f(a))\) and \((b,f(b))\).
Figure \(\PageIndex{6}\): The value \(g(x)\) is the vertical difference between the point \((x,f(x))\) and the point \((x,y)\) on the secant line connecting \((a,f(a))\) and \((b,f(b))\).Since the graph of \(f\) intersects the secant line when \(x=a\) and \(x=b\), we see that \(g(a)=0=g(b)\). Since \(f\) is a differentiable function over \((a,b)\), \(g\) is also a differentiable function over \((a,b)\). Furthermore, since \(f\) is continuous over \([a,b], \, g\) is also continuous over \([a,b]\). Therefore, \(g\) satisfies the criteria of Rolle’s theorem. Consequently, there exists a point \(c∈(a,b)\) such that \(g'(c)=0.\) Since
\[g'(x)=f'(x)−\frac{f(b)−f(a)}{b−a}, \nonumber \]
we see that
\[g'(c)=f'(c)−\frac{f(b)−f(a)}{b−a}. \nonumber \]
Since \(g'(c)=0,\) we conclude that
\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]
□
In the next example, we show how the Mean Value Theorem can be applied to the function \(f(x)=\sqrt{x}\) over the interval \([0,9]\). The method is the same for other functions, although sometimes with more interesting consequences.
Example \(\PageIndex{2}\): Verifying that the Mean Value Theorem Applies
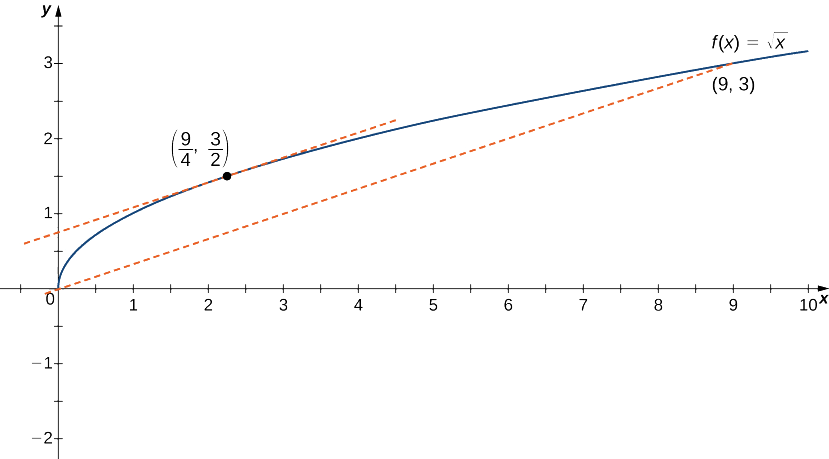
For \(f(x)=\sqrt{x}\) over the interval \([0,9]\), show that \(f\) satisfies the hypothesis of the Mean Value Theorem, and therefore there exists at least one value \(c∈(0,9)\) such that \(f′(c)\) is equal to the slope of the line connecting \((0,f(0))\) and \((9,f(9))\). Find these values \(c\) guaranteed by the Mean Value Theorem.
Solution
We know that \(f(x)=\sqrt{x}\) is continuous over \([0,9]\) and differentiable over \((0,9).\) Therefore, \(f\) satisfies the hypotheses of the Mean Value Theorem, and there must exist at least one value \(c∈(0,9)\) such that \(f′(c)\) is equal to the slope of the line connecting \((0,f(0))\) and \((9,f(9))\) (Figure \(\PageIndex{7}\)). To determine which value(s) of \(c\) are guaranteed, first calculate the derivative of \(f\). The derivative \(f′(x)=\frac{1}{(2\sqrt{x})}\). The slope of the line connecting \((0,f(0))\) and \((9,f(9))\) is given by
\[\frac{f(9)−f(0)}{9−0}=\frac{\sqrt{9}−\sqrt{0}}{9−0}=\frac{3}{9}=\frac{1}{3}. \nonumber \]
We want to find \(c\) such that \(f′(c)=\frac{1}{3}\). That is, we want to find \(c\) such that
\[\frac{1}{2\sqrt{c}}=\frac{1}{3}. \nonumber \]
Solving this equation for \(c\), we obtain \(c=\frac{9}{4}\). At this point, the slope of the tangent line equals the slope of the line joining the endpoints.
One application that helps illustrate the Mean Value Theorem involves velocity. For example, suppose we drive a car for 1 h down a straight road with an average velocity of 45 mph. Let \(s(t)\) and \(v(t)\) denote the position and velocity of the car, respectively, for \(0≤t≤1\) h. Assuming that the position function \(s(t)\) is differentiable, we can apply the Mean Value Theorem to conclude that, at some time \(c∈(0,1)\), the speed of the car was exactly
\[v(c)=s′(c)=\frac{s(1)−s(0)}{1−0}=45\,\text{mph.} \nonumber \]
Example \(\PageIndex{3}\): Mean Value Theorem and Velocity
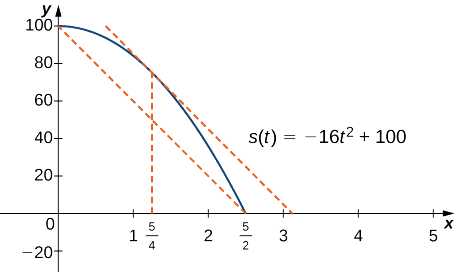
If a rock is dropped from a height of 100 ft, its position \(t\) seconds after it is dropped until it hits the ground is given by the function \(s(t)=−16t^2+100.\)
- Determine how long it takes before the rock hits the ground.
- Find the average velocity \(v_{avg}\) of the rock for when the rock is released and the rock hits the ground.
- Find the time \(t\) guaranteed by the Mean Value Theorem when the instantaneous velocity of the rock is \(v_{avg}.\)
Solution
a. When the rock hits the ground, its position is \(s(t)=0\). Solving the equation \(−16t^2+100=0\) for \(t\), we find that \(t=±\frac{5}{2}sec\). Since we are only considering \(t≥0\), the ball will hit the ground \(\frac{5}{2}\) sec after it is dropped.
b. The average velocity is given by
\[v_{avg}=\frac{s(5/2)−s(0)}{5/2−0}=\frac{0−100}{5/2}=−40\,\text{ft/sec}. \nonumber \]
c. The instantaneous velocity is given by the derivative of the position function. Therefore, we need to find a time \(t\) such that \(v(t)=s′(t)=v_{avg}=−40\) ft/sec. Since \(s(t)\) is continuous over the interval \([0,5/2]\) and differentiable over the interval \((0,5/2),\) by the Mean Value Theorem, there is guaranteed to be a point \(c∈(0,5/2)\) such that
\[s′(c)=\frac{s(5/2)−s(0)}{5/2−0}=−40. \nonumber \]
Taking the derivative of the position function \(s(t)\), we find that \(s′(t)=−32t.\) Therefore, the equation reduces to \(s′(c)=−32c=−40.\) Solving this equation for \(c\), we have \(c=\frac{5}{4}\). Therefore, \(\frac{5}{4}\) sec after the rock is dropped, the instantaneous velocity equals the average velocity of the rock during its free fall: \(−40\) ft/sec.
Exercise \(\PageIndex{2}\)
Suppose a ball is dropped from a height of 200 ft. Its position at time \(t\) is \(s(t)=−16t^2+200.\) Find the time \(t\) when the instantaneous velocity of the ball equals its average velocity.
- Hint
-
First, determine how long it takes for the ball to hit the ground. Then, find the average velocity of the ball from the time it is dropped until it hits the ground.
- Answer
-
\(\frac{5}{2\sqrt{2}}\) sec
Corollaries of the Mean Value Theorem
Let’s now look at three corollaries of the Mean Value Theorem. These results have important consequences, which we use in upcoming sections.
At this point, we know the derivative of any constant function is zero. The Mean Value Theorem allows us to conclude that the converse is also true. In particular, if \(f′(x)=0\) for all \(x\) in some interval \(I\), then \(f(x)\) is constant over that interval. This result may seem intuitively obvious, but it has important implications that are not obvious, and we discuss them shortly.
Corollary 1: Functions with a Derivative of Zero
Let \(f\) be differentiable over an interval \(I\). If \(f′(x)=0\) for all \(x∈I\), then \(f(x)=\) constant for all \(x∈I.\)
Proof
Since \(f\) is differentiable over \(I\), \(f\) must be continuous over \(I\). Suppose \(f(x)\) is not constant for all \(x\) in \(I\). Then there exist \(a,b∈I\), where \(a≠b\) and \(f(a)≠f(b).\) Choose the notation so that \(a<b.\) Therefore,
\[\frac{f(b)−f(a)}{b−a}≠0. \nonumber \]
Since \(f\) is a differentiable function, by the Mean Value Theorem, there exists \(c∈(a,b)\) such that
\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]
Therefore, there exists \(c∈I\) such that \(f′(c)≠0\), which contradicts the assumption that \(f′(x)=0\) for all \(x∈I\).
□
From "Corollary 1: Functions with a Derivative of Zero," it follows that if two functions have the same derivative, they differ by, at most, a constant.
Corollary 2: Constant Difference Theorem
If \(f\) and \(g\) are differentiable over an interval \(I\) and \(f′(x)=g′(x)\) for all \(x∈I\), then \(f(x)=g(x)+C\) for some constant \(C\).
Proof
Let \(h(x)=f(x)−g(x).\) Then, \(h′(x)=f′(x)−g′(x)=0\) for all \(x∈I.\) By Corollary 1, there is a constant \(C\) such that \(h(x)=C\) for all \(x∈I\). Therefore, \(f(x)=g(x)+C\) for all \(x∈I.\)
□
The third corollary of the Mean Value Theorem discusses when a function is increasing and when it is decreasing. Recall that a function \(f\) is increasing over \(I\) if \(f(x_1)<f(x_2)\) whenever \(x_1<x_2\), whereas \(f\) is decreasing over \(I\) if \(f(x_1)>f(x_2)\) whenever \(x_1<x_2\). Using the Mean Value Theorem, we can show that if the derivative of a function is positive, then the function is increasing; if the derivative is negative, then the function is decreasing (Figure \(\PageIndex{9}\)). We make use of this fact in the next section, where we show how to use the derivative of a function to locate local maximum and minimum values of the function, and how to determine the shape of the graph.
This fact is important because it means that for a given function \(f\), if there exists a function \(F\) such that \(F′(x)=f(x)\); then, the only other functions that have a derivative equal to \(f\) are \(F(x)+C\) for some constant \(C\). We discuss this result in more detail later in the chapter.
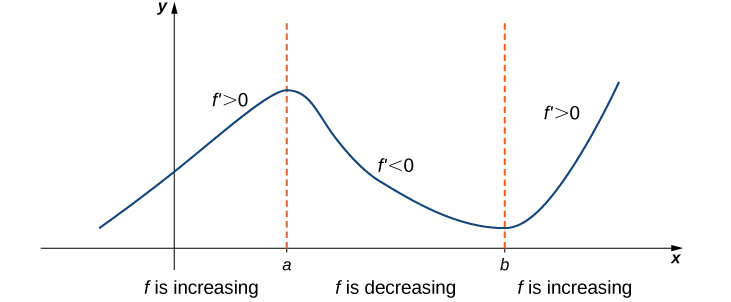
Corollary 3: Increasing and Decreasing Functions
Let \(f\) be continuous over the closed interval \([a,b]\) and differentiable over the open interval \((a,b)\).
- If \(f′(x)>0\) for all \(x∈(a,b)\), then \(f\) is an increasing function over \([a,b].\)
- If \(f′(x)<0\) for all \(x∈(a,b)\), then \(f\) is a decreasing function over \([a,b].\)
Proof
We will prove i.; the proof of ii. is similar. Suppose \(f\) is not an increasing function on \(I\). Then there exist \(a\) and \(b\) in \(I\) such that \(a<b\), but \(f(a)≥f(b)\). Since \(f\) is a differentiable function over \(I\), by the Mean Value Theorem there exists \(c∈(a,b)\) such that
\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]
Since \(f(a)≥f(b)\), we know that \(f(b)−f(a)≤0\). Also, \(a<b\) tells us that \(b−a>0.\) We conclude that
\[f′(c)=\frac{f(b)−f(a)}{b−a}≤0. \nonumber \]
However, \(f′(x)>0\) for all \(x∈I\). This is a contradiction, and therefore \(f\) must be an increasing function over \(I\).
□
Key Concepts
- If \(f\) is continuous over \([a,b]\) and differentiable over \((a,b)\) and \(f(a)=f(b)\), then there exists a point \(c∈(a,b)\) such that \(f′(c)=0.\) This is Rolle’s theorem.
- If \(f\) is continuous over \([a,b]\) and differentiable over \((a,b)\), then there exists a point \(c∈(a,b)\) such that \[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \] This is the Mean Value Theorem.
- If \(f'(x)=0\) over an interval \(I\), then \(f\) is constant over \(I\).
- If two differentiable functions \(f\) and \(g\) satisfy \(f′(x)=g′(x)\) over \(I\), then \(f(x)=g(x)+C\) for some constant \(C\).
- If \(f′(x)>0\) over an interval \(I\), then \(f\) is increasing over \(I\). If \(f′(x)<0\) over \(I\), then \(f\) is decreasing over \(I\).
Glossary
- mean value theorem
-
if \(f\) is continuous over \([a,b]\) and differentiable over \((a,b)\), then there exists \(c∈(a,b)\) such that \(f′(c)=\frac{f(b)−f(a)}{b−a}\)
- rolle’s theorem
- if \(f\) is continuous over \([a,b]\) and differentiable over \((a,b)\), and if \(f(a)=f(b)\), then there exists \(c∈(a,b)\) such that \(f′(c)=0\)


