1.7: The Pigeonhole Principle
- Page ID
- 7143
A key step in many proofs consists of showing that two possibly different values are in fact the same. The Pigeonhole principle can sometimes help with this.
Suppose that \(n+1\) (or more) objects are put into \(n\) boxes. Then some box contains at least two objects.
- Proof
-
Suppose each box contains at most one object. Then the total number of objects is at most \(1+1+\cdots+1=n\), a contradiction.
This seemingly simple fact can be used in surprising ways. The key typically is to put objects into boxes according to some rule, so that when two objects end up in the same box it is because they have some desired relationship.
Among any 13 people, at least two share a birth month.
Label 12 boxes with the names of the months. Put each person in the box labeled with his or her birth month. Some box will contain at least two people, who share a birth month.
Suppose 5 pairs of socks are in a drawer. Picking 6 socks guarantees that at least one pair is chosen.
Label the boxes by "the pairs'' (e.g., the red pair, the blue pair, the argyle pair,…). Put the 6 socks into the boxes according to description.
Some uses of the principle are not nearly so straightforward.
Suppose \(a_1,\ldots,a_n\) are integers. Then some "consecutive sum'' \(a_k+a_{k+1}+a_{k+2}+\cdots+a_{k+m}\) is divisible by \(n\).
Consider these \(n\) sums: \[\eqalign{ s_1&=a_1\cr s_2&=a_1+a_2\cr s_3&=a_1+a_2+a_3\cr &\vdots\cr s_n&=a_1+a_2+\cdots+a_n\cr }\nonumber\]
These are all consecutive sums, so if one of them is divisible by \(n\) we are done. If not, dividing each by \(n\) leaves a non-zero remainder, \(r_1=s_1\bmod n\), \(r_2=s_2\bmod n\), and so on. These remainders have values in \(\{1,2,3,\ldots,n-1\}\). Label \(n-1\) boxes with these \(n-1\) values; put each of the \(n\) sums into the box labeled with its remainder mod \(n\). Two sums end up in the same box, meaning that \(s_i\bmod n=s_j\bmod n\) for some \(j>i\); hence \(s_j-s_i\) is divisible by \(n\), and \(s_j-s_i=a_{i+1}+a_{i+2}+\cdots+a_j\), as desired.
A similar argument provides a proof of the Chinese Remainder Theorem.
If \(m\) and \(n\) are relatively prime, and \(0\le a< m\) and \(0\le b< n\), then there is an integer \(x\) such that \(x\bmod m=a\) and \(x\bmod n=b\).
- Proof
-
Consider the integers \(a,a+m,a+2m,\ldots a+(n-1)m\), each with remainder \(a\) when divided by \(m\). We wish to show that one of these integers has remainder \(b\) when divided by \(n\), in which case that number satisfies the desired property.
For a contradiction, suppose not. Let the remainders be \(r_0=a\bmod n\), \(r_1=a+m\bmod n\),…, \(r_{n-1}=a+(n-1)m\bmod n\). Label \(n-1\) boxes with the numbers \(0,1,2,3,\ldots,b-1,b+1,\ldots n-1\). Put each \(r_i\) into the box labeled with its value. Two remainders end up in the same box, say \(r_i\) and \(r_j\), with \(j>i\), so \(r_i=r_j=r\). This means that \[a+im=q_1n+r\quad\hbox{and}\quad a+jm=q_2n+r.\nonumber\]
Hence \[\eqalign{ a+jm-(a+im)&=q_2n+r-(q_1n+r)\cr (j-i)m&=(q_2-q_1)n.\cr }\nonumber\]
Since \(n\) is relatively prime to \(m\), this means that \(n | (j-i)\). But since \(i\) and \(j\) are in \(\{0,1,2,\ldots,n-1\}\), \(0< j-i< n\), so \(n\cancel{|}(j-i)\). This contradiction finishes the proof.
More general versions of the Pigeonhole Principle can be proved by essentially the same method. A natural generalization would be something like this: If \(X\) objects are put into \(n\) boxes, some box contains at least \(m\) objects. For example:
Suppose that \(r_1,\ldots,r_n\) are positive integers. If \(X\ge(\sum_{i=1}^n r_i) -n + 1\) objects are put into \(n\) boxes labeled \(1,2,3,\ldots,n\), then some box labeled \(i\) contains at least \(r_i\) objects.
- Proof
-
Suppose not. Then the total number of objects in the boxes is at most \((r_1-1)+(r_2-1)+(r_3-1)+\cdots+(r_n-1)=(\sum_{i=1}^n r_i) -n < X\), a contradiction.
This full generalization is only occasionally needed; often this simpler version is sufficient:
Suppose \(r>0\) and \(X\ge n(r-1)+1\) objects are placed into \(n\) boxes. Then some box contains at least \(r\) objects.
- Proof
-
Apply the previous theorem with \(r_i=r\) for all \(i\).
\[\bullet\quad\bullet\quad\bullet\nonumber\]
Here is a simple application of the Pigeonhole Principle that leads to many interesting questions.
Suppose 6 people are gathered together; then either 3 of them are mutually acquainted, or 3 of them are mutually unacquainted.
We turn this into a graph theory question: Consider the graph consisting of 6 vertices, each connected to all the others by an edge, called the complete graph on \(6\) vertices, and denoted \(K_6\); the vertices represent the people. Color an edge red if the people represented by its endpoints are acquainted, and blue if they are not acquainted. Any choice of 3 vertices defines a triangle; we wish to show that either there is a red triangle or a blue triangle.
Consider the five edges incident at a single vertex \(v\); by the Pigeonhole Principle (the version in corollary 1.6.7, with \(r=3\), \(X=2(3-1)+1=5\)), at least three of them are the same color, call it color \(C\); call the other color \(D\). Let the vertices at the other ends of these three edges be \(v_1\), \(v_2\), \(v_3\). If any of the edges between these vertices have color \(C\), there is a triangle of color \(C\): if the edge connects \(v_i\) to \(v_j\), the triangle is formed by \(v\), \(v_i\), and \(v_j\). If this is not the case, then the three vertices \(v_1\), \(v_2\), \(v_3\) are joined by edges of color \(D\), and form a triangle of color \(D\).
The number 6 in this example is special: with 5 or fewer vertices it is not true that there must be a monochromatic triangle, and with more than 6 vertices it is true. To see that it is not true for 5 vertices, we need only show an example, as in Figure \(\PageIndex{1}\).
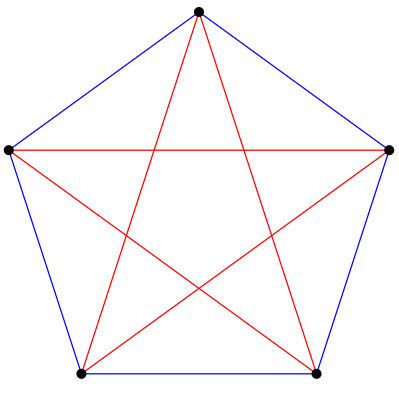
The Ramsey number \(R(i)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with two colors, there is a monochromatic complete graph on \(i\) vertices, \(K_i\), contained within \(K_n\). The example shows that \(R(3)=6\).
More generally, \(R(i,j)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with two colors, say \(C_1\) and \(C_2\), either there is a \(K_i\) contained within \(K_n\) all of whose edges are color \(C_1\), or there is a \(K_j\) contained within \(K_n\) all of whose edges are color \(C_2\). Using this notion, \(R(k)=R(k,k)\). More generally still, \(R(i_1,i_2,\ldots,i_m)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with \(m\) colors, \(C_1,…,C_m\), then for some \(j\) there is a \(K_{i_j}\) contained in \(K_n\) all of whose edges are color \(C_j\).
Ramsey proved that in all of these cases, there actually is such a number \(n\). Generalizations of this problem have led to the subject called Ramsey Theory.
Computing any particular value \(R(i,j)\) turns out to be quite difficult; Ramsey numbers are known only for a few small values of \(i\) and \(j\), and in some other cases the Ramsey number is bounded by known numbers. Typically in these cases someone has exhibited a \(K_m\) and a coloring of the edges without the existence of a monochromatic \(K_i\) or \(K_j\) of the desired color, showing that \(R(i,j)>m\); and someone has shown that whenever the edges of \(K_n\) have been colored, there is a \(K_i\) or \(K_j\) of the correct color, showing that \(R(i,j)\le n\).


