7.2: Representation Formula
- Page ID
- 2163
In the following we assume that \(\Omega\), the function \(\phi\) which appears in the definition of the fundamental solution and the potential function \(u\) considered are sufficiently regular such that the following calculations make sense, see [6] for generalizations. This is the case if \(\Omega\) is bounded, \(\partial\Omega\) is in \(C^1\), \(\phi\in C^2(\overline{\Omega})\) for each fixed \(y\in\Omega\) and \(u\in C^2(\overline{\Omega})\).
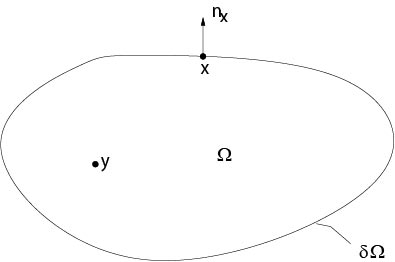
Figure 7.2.1: Notations to Green's identity
Theorem 7.1. Let \(u\) be a potential function and \(\gamma\) a fundamental solution, then for each fixed \(y\in\Omega\)
$$
u(y)=\int_{\partial\Omega}\left(\gamma (x,y)\frac{\partial u(x)}{\partial n_x}-u(x)\frac{\partial \gamma(x,y)}{\partial n_x}\right)\ dS_x.
$$
Proof. Let \(B_\rho(y)\subset\Omega\) be a ball. Set \(\Omega_\rho(y)=\Omega\setminus B_\rho(y)\). See Figure 7.2.2 for notations.
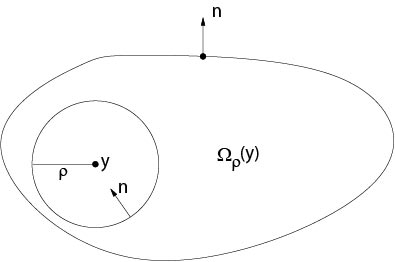
Figure 7.2.2: Notations to Theorem 7.1
From Green's formula, for \(u,\ v\in C^2(\overline{\Omega})\),
$$
\int_{\Omega_\rho(y)}\ (v\triangle u-u\triangle v)\ dx=\int_{\partial\Omega_\rho(y)}\ \left(v\frac{\partial u}{\partial n}-u\frac{\partial v}{\partial n}\right)\ dS
$$
we obtain, if \(v\) is a fundamental solution and \(u\) a potential function,
$$
\int_{\partial\Omega_\rho(y)}\ \left(v\frac{\partial u}{\partial n}-u\frac{\partial v}{\partial n}\right)\ dS=0.
$$
Thus we have to consider
\begin{eqnarray*}
\int_{\partial\Omega_{\rho}(y)}\ v\frac{\partial u}{\partial n}\ dS&=&\int_{\partial\Omega}\ v\frac{\partial u}{\partial n}\ dS+\int_{\partial B_\rho(y)}\ v\frac{\partial u}{\partial n}\ dS\\
\int_{\partial\Omega_{\rho}(y)}\ u\frac{\partial v}{\partial n}\ dS&=&\int_{\partial\Omega}\ u\frac{\partial v}{\partial n}\ dS+\int_{\partial B_\rho(y)}\ u\frac{\partial v}{\partial n}\ dS.
\end{eqnarray*}
We estimate the integrals over \(\partial B_\rho(y)\):
(i)
\begin{eqnarray*}
\left|\int_{\partial B_\rho(y)}\ v\frac{\partial u}{\partial n}\ dS\right|&\le&M\int_{\partial B_\rho(y)}\ |v|\ dS\\
&\le&M\left(\int_{\partial B_\rho(y)}\ s(\rho)\ dS+C\omega_n\rho^{n-1}\right),
\end{eqnarray*}
where
\begin{eqnarray*}
M&=&M(y)=\sup_{B_{\rho_0}(y)}|\partial u/\partial n|,\ \ \rho\le\rho_0,\\
C&=&C(y)=\sup_{x\in B_{\rho_0}(y)}|\phi(x,y)|.
\end{eqnarray*}
From the definition of \(s(\rho)\) we get the estimate as \(\rho\to 0\)
\begin{equation}
\label{ell1}
\int_{\partial B_\rho(y)}\ v\frac{\partial u}{\partial n}\ dS=\left\{\begin{array}{r@{\quad:\quad}l}
O(\rho|\ln\rho|)&n=2\\
O(\rho)&n\ge3.
\end{array}\right.
\end{equation}
(ii) Consider the case \(n\ge3\), then
\begin{eqnarray*}
\int_{\partial B_\rho(y)}\ u\frac{\partial v}{\partial n}\ dS&=&
\frac{1}{\omega_n}\int_{\partial B_\rho(y)}\ u\frac{1}{\rho^{n-1}}\ dS+\int_{\partial B_\rho(y)}\ u\frac{\partial \phi}{\partial n}\ dS\\
&=&\frac{1}{\omega_n\rho^{n-1}}\int_{\partial B_\rho(y)}\ u\ dS+O(\rho^{n-1})\\
&=&\frac{1}{\omega_n\rho^{n-1}}u(x_0)\int_{\partial B_\rho(y)}\ dS+O(\rho^{n-1}),\\ &=&u(x_0)+O(\rho^{n-1}).
\end{eqnarray*}
for an \(x_0\in\partial B_\rho(y)\).
Combining this estimate and (\ref{ell1}), we obtain the representation formula of the theorem.
\(\Box\)
Corollary. Set \(\phi\equiv 0\) and \(r=|x-y|\) in the representation formula of Theorem 7.1, then
\begin{eqnarray}
\label{ell2}
u(y)&=&\frac{1}{2\pi}\int_{\partial\Omega}\ \left(\ln r\frac{\partial u}{\partial n_x}-u\frac{\partial(\ln r)}{\partial n_x}\right)\ dS_x,\ \ n=2,\\
\label{ell3}
u(y)&=&\frac{1}{(n-2)\omega_n}\int_{\partial\Omega}\ \left(\frac{1}{r^{n-2}}\frac{\partial u}{\partial n_x}-u\frac{\partial(r^{2-n})}{\partial n_x}\right)\ dS_x,\ \ n\ge3.
\end{eqnarray}
Contributors and Attributions
Integrated by Justin Marshall.


