7.5: Inhomogeneous Equation
- Page ID
- 2166
Here we consider solutions \(u\in C^2(\Omega)\cap C(\overline{\Omega})\) of
\begin{eqnarray}
\label{DI1}
-\triangle u&=&f(x)\ \ \mbox{in}\ \Omega\\
\label{DI2}
u&=&0\ \ \ \mbox{on}\ \partial\Omega,
\end{eqnarray}
where \(f\) is given.
We need the following lemma concerning volume potentials. We assume that \(\Omega\) is bounded and sufficiently regular such that all the following integrals exist. See [6] for generalizations concerning these assumptions.
Let for \(x\in\mathbb{R}^n\), \(n\ge3\),
$$
V(x)=\int_\Omega\ f(y)\frac{1}{|x-y|^{n-2}}\ dy
$$
and set in the two-dimensional case
$$
V(x)=\int_\Omega\ f(y)\ln\left(\frac{1}{|x-y|}\right)\ dy.
$$
We recall that \(\omega_n=|\partial B_1(0)|\).
Lemma.
(i) Assume \(f\in C(\Omega)\). Then \(V\in C^1(\mathbb{R}^n)\) and
\begin{eqnarray*}
V_{x_i}(x)&=& \int_\Omega\ f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|^{n-2}}\right)\ dy,\ \ \mbox{if}\ n\ge3,\\
V_{x_i}(x)&=&\int_\Omega\ f(y)\frac{\partial}{\partial x_i} \left(\ln\left(\frac{1}{|x-y|}\right)\right)\ dy\ \ \mbox{if}\ n=2.
\end{eqnarray*}
(ii) If \(f\in C^1(\Omega)\), then \(V\in C^2(\Omega)\) and
\begin{eqnarray*}
\triangle V&=&-(n-2)\omega_n f(x),\ x\in\Omega,\ n\ge 3\\
\triangle V&=&-2\pi f(x),\ x\in\Omega,\ n=2.
\end{eqnarray*}
Proof. To simplify the presentation, we consider the case \(n=3\).
(i) The first assertion follows since we can change differentiation with integration since the differentiate integrand is weakly singular, see an exercise.
(ii) We will differentiate at \(x\in\Omega\). Let \(B_\rho\) be a fixed ball such that \(x\in B_\rho\), \(\rho\) sufficiently small such that \(B_\rho\subset\Omega\). Then, according to (i)
and since we have the identity
$$
\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)=-\frac{\partial}{\partial y_i}\left(\frac{1}{|x-y|}\right)
$$
which implies that
$$
f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)=-\frac{\partial}{\partial y_i}\left(f(y)\frac{1}{|x-y|}\right)+f_{y_i}(y)\frac{1}{|x-y|},
$$
we obtain
\begin{eqnarray*}
V_{x_i}(x)&=&\int_\Omega\ f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)\ dy\\
&=&\int_{\Omega\setminus B_\rho}\ f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)\ dy+\int_{B_\rho}\ f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)\ dy\\
&=&\int_{\Omega\setminus B_\rho}\ f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)\ dy\\
&&+\int_{B_\rho}\ \left(-\frac{\partial}{\partial y_i}\left(f(y)\frac{1}{|x-y|}\right)+f_{y_i}(y)\frac{1}{|x-y|}\right)\ dy\\
&=&\int_{\Omega\setminus B_\rho}\ f(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)\ dy\\
&&+\int_{B_\rho}\ f_{y_i}(y)\frac{1}{|x-y|}\ dy-\int_{\partial B_\rho}\ f(y)\frac{1}{|x-y|}n_i\ dS_y,
\end{eqnarray*}
where \(n\) is the exterior unit normal at \(\partial B_\rho\). It follows that the first and second integral is in \(C^1(\Omega)\). The second integral is also in \(C^1(\Omega)\) according to (i) and since \(f\in C^1(\Omega)\) by assumption.
Because of \(\triangle_x(|x-y|^{-1})=0,\ x\not=y\), it follows
\begin{eqnarray*}
\triangle V&=&\int_{B_\rho}\ \sum_{i=1}^n f_{y_i}(y)\frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)\ dy\\
&&\ -\int_{\partial B_\rho}\ f(y)\sum_{i=1}^n \frac{\partial}{\partial x_i}\left(\frac{1}{|x-y|}\right)n_i\ dS_y.
\end{eqnarray*}
Now we choose for \(B_\rho\) a ball with the center at \(x\), then
$$
\triangle V=I_1+I_2,
$$
where
\begin{eqnarray*}
I_1&=&\int_{B_\rho(x)}\ \sum_{i=1}^n f_{y_i}(y)\frac{y_i-x_i}{|x-y|^3}\ dy\\
I_2&=&-\int_{\partial B_\rho(x)}\ f(y)\frac{1}{\rho^2} \ dS_y.
\end{eqnarray*}
We recall that \(n\cdot(y-x)=\rho\) if \(y\in\partial B_\rho(x)\). It is \(I_1=O(\rho)\) as \(\rho\to 0\) and for \(I_2\) we obtain from the mean value theorem of the integral calculus that for a \(\overline{y}\in\partial B_\rho(x)\)
\begin{eqnarray*}
I_2&=&-\frac{1}{\rho^2}f(\overline{y})\int_{\partial B_\rho(x)}\ dS_y\\
&=&-\omega_nf(\overline{y}),
\end{eqnarray*}
which implies that \(\lim_{\rho\to0} I_2=-\omega_nf(x)\).
\(\Box\)
In the following we assume that Green's function exists for the domain \(\Omega\), which is the case if \(\Omega\) is a ball.
Theorem 7.3. Assume \(f\in C^1(\Omega)\cap C(\overline{\Omega})\). Then
$$
u(x)=\int_\Omega\ G(x,y)f(y)\ dy
$$
is the solution of the inhomogeneous problem (\ref{DI1}), (\ref{DI2}).
Proof. For simplicity of the presentation let \(n=3\). We will show that
$$
u(x):=\int_\Omega\ G(x,y) f(y)\ dy
$$ is a solution of (7.3.1.1), (7.3.1.2). Since
$$
G(x,y)=\frac{1}{4\pi|x-y|}+\phi(x,y),
$$
where \(\phi\) is a potential function with respect to \(x\) or \(y\), we obtain from the above lemma that
\begin{eqnarray*}
\triangle u&=&\frac{1}{4\pi}\triangle\int_\Omega\ f(y)\frac{1}{|x-y|}\ dy+\int_\Omega\triangle_x\phi (x,y)f(y)\ dy\\
&=&-f(x),
\end{eqnarray*}
where \(x\in\Omega\). It remains to show that \(u\) achieves its boundary values. That is, for fixed \(x_0\in\partial\Omega\) we will prove that
$$
\lim_{x\to x_0,\ x\in\Omega} u(x)=0.
$$
Set
$$
u(x)=I_1+I_2,
$$
where
\begin{eqnarray*}
I_1(x)&=&\int_{\Omega\setminus B_\rho(x_0)}\ G(x,y)f(y)\ dy,\\
I_2(x)&=&\int_{\Omega\cap B_\rho(x_0)}\ G(x,y)f(y)\ dy.
\end{eqnarray*}
Let \(M=\max_{\overline{\Omega}}|f(x)|\). Since
$$
G(x,y)= \frac{1}{4\pi}\frac{1}{|x-y|}+\phi(x,y),
$$
we obtain, if \(x\in B_\rho(x_0)\cap\Omega\),
\begin{eqnarray*}
|I_2|&\le&\frac{M}{4\pi}\int_{\Omega\cap B_\rho(x_0)}\ \frac{dy}{|x-y|}+O(\rho^2)\\
&\le&\frac{M}{4\pi}\int_{B_{2\rho(x)}}\ \frac{dy}{|x-y|}+O(\rho^2)\\
&=&O(\rho^2)
\end{eqnarray*}
as \(\rho\to0\). Consequently for given \(\epsilon\) there is a \(\rho_0=\rho_0(\epsilon)>0\) such that
$$
|I_2|<\frac{\epsilon}{2}\ \ \mbox{for all}\ \ 0<\rho\le\rho_0.
$$
For each fixed \(\rho\), \(0<\rho\le\rho_0\), we have
$$
\lim_{x\to x_0,\ x\in\Omega} I_1(x)=0
$$
since \(G(x_0,y)=0\) if \(y\in\Omega\setminus B_\rho(x_0)\) and \(G(x,y)\) is uniformly continuous in \(x\in B_{\rho/2}(x_0)\cap\Omega\) and \(y\in\Omega\setminus B_\rho(x_0)\), see Figure 7.5.1.
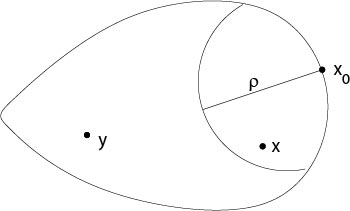
Figure 7.5.1: Proof of Theorem 7.3
\(\Box\)
Remark. For the proof of (ii) in the above lemma it is sufficient to assume that \(f\) is H\"older continuous. More precisely, let
\(f\in C^{\lambda}(\Omega)\), \(0<\lambda<1\), then \(V\in C^{2,\lambda}(\Omega)\), see for instance [9].
Contributors and Attributions
Integrated by Justin Marshall.


