11.1: Bases in \(\Re^{n}\)

In review question 2, chapter 10 you checked that

\[ \Re^{n} = span \left\{ \begin{pmatrix}1\\0\\ \vdots \\ 0\end{pmatrix}, \begin{pmatrix}0\\1\\ \vdots \\ 0\end{pmatrix}, \ldots, \begin{pmatrix}0\\0\\ \vdots \\ 1\end{pmatrix}\right\}, \]

and that this set of vectors is linearly independent. (If you didn't do that problem, check this before reading any further!) So this set of vectors is a basis for \(\Re^{n}\), and \(\dim \Re^{n}=n\). This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\Re^{n}\). The vector with a one in the \(i\)th position and zeros everywhere else is written \(e_{i}\). (You could also view it as the function \(\{1,2,\ldots,n\}\to \mathbb{R}\) where \(e_{i}(j)=1\) if \(i=j\) and \(0\) if \(i\neq j\).) It points in the direction of the \(i^{th}\) coordinate axis, and has unit length. In multivariable calculus classes, this basis is often written \(\{ i, j, k \}\) for \(\Re^{3}\). 

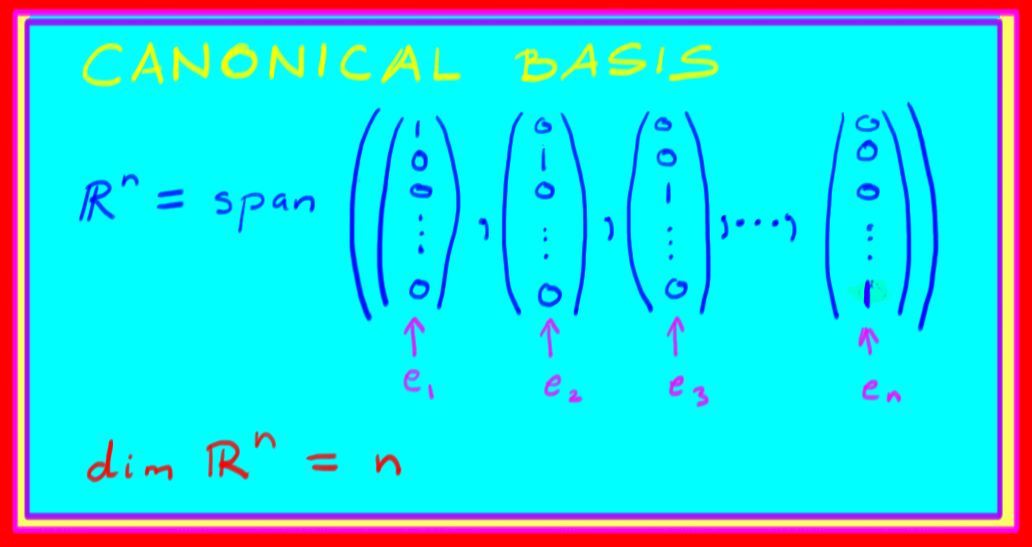
Note that it is often convenient to order basis elements, so rather than writing a set of vectors, we would write a list. This is called an ordered basis. For example, the canonical ordered basis for \(\mathbb{R^{n}}\) is \((e_{1},e_{2},\ldots,e_{n})\). The possibility to reorder basis vectors is not the only way in which bases are non-unique: 

Remark (Bases are not unique)

While there exists a unique way to express a vector in terms of any particular basis, bases themselves are far from unique.

For example, both of the sets:

\[ \left\{ \begin{pmatrix}1\\0\end{pmatrix}, \begin{pmatrix}0\\1\end{pmatrix} \right\} \textit{ and } \left\{ \begin{pmatrix}1\\1\end{pmatrix}, \begin{pmatrix}1\\-1\end{pmatrix} \right\} \]

are bases for \(\Re^{2}\). Rescaling any vector in one of these sets is already enough to show that \(\Re^{2}\) has infinitely many bases. But even if we require that all of the basis vectors have unit length, it turns out that there are still infinitely many bases for \(\Re^{2}\) (see review question 3).

To see whether a collection of vectors \(S=\{v_{1}, \ldots, v_{m} \}\) is a basis for \(\Re^{n}\), we have to check that they are linearly independent and that they span \(\Re^{n}\). From the previous discussion, we also know that \(m\) must equal \(n\), so lets assume \(S\) has \(n\) vectors. If \(S\) is linearly independent, then there is no non-trivial solution of the equation

\[0 = x^{1}v_{1}+\cdots + x^{n}v_{n}.\]

Let \(M\) be a matrix whose columns are the vectors \(v_{i}\) and \(X\) the column vector with entries \(x^{i}\). Then the above equation is equivalent to requiring that there is a unique solution to

\[MX=0\, .\]

To see if \(S\) spans \(\Re^{n}\), we take an arbitrary vector \(w\) and solve the linear system

\[w=x^{1}v_{1}+\cdots + x^{n}v_{n}\]

in the unknowns \(x^{i}\). For this, we need to find a unique solution for the linear system \(MX=w\).

Thus, we need to show that \(M^{-1}\) exists, so that

\[ X=M^{-1}w \]

is the unique solution we desire. Then we see that \(S\) is a basis for \(V\) if and only if \(\det M\neq 0\).

Theorem

Let \(S=\{v_{1}, \ldots, v_{m} \}\) be a collection of vectors in \(\Re^{n}\). Let \(M\) be the matrix whose columns are the vectors in \(S\). Then \(S\) is a basis for \(V\) if and only if \(m\) is the dimension of \(V\) and 

\[\det M \neq 0.\]

Remark
Also observe that \(S\) is a basis if and only if \({\rm RREF}(M)=I\).

Example 113

Let 
\[
S=\left\{ \begin{pmatrix}1\\0\end{pmatrix}, \begin{pmatrix}0\\1\end{pmatrix} \right\} \textit{ and }
T=\left\{ \begin{pmatrix}1\\1\end{pmatrix}, \begin{pmatrix}1\\-1\end{pmatrix} \right\}.
\]
Then set \(M_{S}=\begin{pmatrix}
1 & 0\\
0 & 1\\
\end{pmatrix}\). Since \(\det M_{S}=1\neq 0\), then \(S\) is a basis for \(\Re^{2}\).\\
Likewise, set \(M_{T}=\begin{pmatrix}
1 & 1\\
1 & -1\\
\end{pmatrix}\). Since \(\det M_{T}=-2\neq 0\), then \(T\) is a basis for \(\Re^{2}\).

Contributor

• David Cherney, Tom Denton, and Andrew Waldron (UC Davis)