2.3: Modeling with Linear Functions
- Page ID
- 13836
When modeling scenarios with a linear function and solving problems involving quantities changing linearly, we typically follow the same problem solving strategies that we would use for any type of function:
Problem Solving Strategy
- Identify changing quantities, and then carefully and clearly define descriptive variables to represent those quantities. When appropriate, sketch a picture or define a coordinate system.
- Carefully read the problem to identify important information. Look for information giving values for the variables, or values for parts of the functional model, like slope and initial value.
- Carefully read the problem to identify what we are trying to find, identify, solve, or interpret.
- Identify a solution pathway from the provided information to what we are trying to find. Often this will involve checking and tracking units, building a table or even finding a formula for the function being used to model the problem.
- When needed, find a formula for the function.
- Solve or evaluate using the formula you found for the desired quantities.
- Reflect on whether your answer is reasonable for the given situation and whether it makes sense mathematically.
- Clearly convey your result using appropriate units, and answer in full sentences when appropriate.
Example \(\PageIndex{1}\)
Emily saved up $3500 for her summer visit to Seattle. She anticipates spending $400 each week on rent, food, and fun. Find and interpret the horizontal intercept and determine a reasonable domain and range for this function.
Solution
In the problem, there are two changing quantities: time and money. The amount of money she has remaining while on vacation depends on how long she stays. We can define our variables, including units.
Output: \(M\), money remaining, in dollars
Input: \(t\), time, in weeks
Reading the problem, we identify two important values. The first, $3500, is the initial value for \(M\). The other value appears to be a rate of change – the units of dollars per week match the units of our output variable divided by our input variable. She is spending money each week, so you should recognize that the amount of money remaining is decreasing each week and the slope is negative.
To answer the first question, looking for the horizontal intercept, it would be helpful to have an equation modeling this scenario. Using the intercept and slope provided in the problem, we can write the equation: \[M(t)=3500-400t\nonumber \]
To find the horizontal intercept, we set the output to zero, and solve for the input:
\[\begin{array} {rcl} {0} &= & {3500 - 400t} \\ {t} &= & { \dfrac{3500}{400} = 8.75} \end{array}\nonumber \]
The horizontal intercept is 8.75 weeks. Since this represents the input value where the output will be zero, interpreting this, we could say: Emily will have no money left after 8.75 weeks.
When modeling any real life scenario with functions, there is typically a limited domain over which that model will be valid – almost no trend continues indefinitely. In this case, it certainly doesn’t make sense to talk about input values less than zero. It is also likely that this model is not valid after the horizontal intercept (unless Emily’s going to start using a credit card and go into debt).
The domain represents the set of input values and so the reasonable domain for this function is \(0 \le t \le 8.75\).
However, in a real world scenario, the rental might be weekly or nightly. She may not be able to stay a partial week and so all options should be considered. Emily could stay in Seattle for 0 to 8 full weeks (and a couple of days), but would have to go into debt to stay 9 full weeks, so restricted to whole weeks, a reasonable domain without going in to debt would be \(0 \le t \le 8\), or \(0 \le t \le 9\) if she went into debt to finish out the last week.
The range represents the set of output values and she starts with $3500 and ends with $0 after 8.75 weeks so the corresponding range is \(0 \le M(t) \le 3500\). If we limit the rental to whole weeks, however, the range would change. If she left after 8 weeks because she didn’t have enough to stay for a full 9 weeks, she would have \(M(8) = 3500 - 400 (8) = $300\) dollars left after 8 weeks, giving a range of \(300 \le M(t) \le 3500\). If she wanted to stay the full 9 weeks she would be $100 in debt giving a range of \(-100 \le M(t) \le 3500\).
Most importantly remember that domain and range are tied together, and what ever you decide is most appropriate for the domain (the independent variable) will dictate the requirements for the range (the dependent variable).
Exercise \(\PageIndex{1}\)
A database manager is loading a large table from backups. Getting impatient, she notices 1.2 million rows had been loaded. Ten minutes later, 2.5 million rows had been loaded. How much longer will she have to wait for all 80 million rows to load?
- Answer
-
Letting \(t\) be the number of minutes since she got impatient, and N be the number rows loaded, in millions, we have two points: (0, 1.2) and (10, 2.5).
The slope is \(m=\dfrac{2.5-1.2}{10-0} =\dfrac{1.3}{10} =0.13\) million rows per minute.
We know the \(N\) intercept, so we can write the equation:
\[N=0.13t+1.2\nonumber \]
To determine how long she will have to wait, we need to solve for when \(N = 80\).
\[N = 0.13t + 1.2 = 80\nonumber \]
\[0.13t = 78.8\nonumber \]
\[t = \dfrac{78.8}{0.13} = 606\nonumber \]. She’ll have to wait another 606 minutes, about 10 hours.
Example \(\PageIndex{2}\)
Jamal is choosing between two moving companies. The first, U-Haul, charges an up-front fee of $20, then 59 cents a mile. The second, Budget, charges an up-front fee of $16, then 63 cents a mile(Rates retrieved Aug 2, 2010 from www.budgettruck.com and http://www.uhaul.com/). When will U-Haul be the better choice for Jamal?
Solution
The two important quantities in this problem are the cost, and the number of miles that are driven. Since we have two companies to consider, we will define two functions:
Input: \(m\), miles driven
Outputs:
\(Y(m)\): cost, in dollars, for renting from U-Haul
\(B(m)\): cost, in dollars, for renting from Budget
Reading the problem carefully, it appears that we were given an initial cost and a rate of change for each company. Since our outputs are measured in dollars but the costs per mile given in the problem are in cents, we will need to convert these quantities to match our desired units: $0.59 a mile for U-Haul, and $0.63 a mile for Budget.
Looking to what we’re trying to find, we want to know when U-Haul will be the better choice. Since all we have to make that decision from is the costs, we are looking for when U-Haul will cost less, or when \(Y(m) < B(m)\). The solution pathway will lead us to find the equations for the two functions, find the intersection, then look to see where the \(Y(m)\) function is smaller. Using the rates of change and initial charges, we can write the equations:
\[Y(m) = 20 + 0.59m\nonumber \]
\[B(m) = 16 + 0.63m\nonumber \]
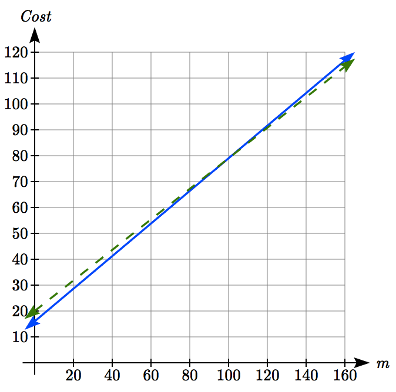
These graphs are sketched to the right, with Y(m) drawn dashed.
To find the intersection, we set the equations equal and solve:
\[\begin{array} {rcl} {Y(m)} &= & {B(m)} \\ {20 + 0.59m} &= & {16 + 0.63m} \\ {4} &= & {0.04m} \\ {m} &= & {100} \end{array}\nonumber \]
This tells us that the cost from the two companies will be the same if 100 miles are driven. Either by looking at the graph, or noting that \(Y(m)\) is growing at a slower rate, we can conclude that U-Haul will be the cheaper price when more than 100 miles are driven.
Example \(\PageIndex{3}\)
A town’s population has been growing linearly. In 2004 the population was 6,200. By 2009 the population had grown to 8,100. If this trend continues,
- Predict the population in 2013
- When will the population reach 15000?
Solution
The two changing quantities are the population and time. While we could use the actual year value as the input quantity, doing so tends to lead to very ugly equations, since the vertical intercept would correspond to the year 0, more than 2000 years ago!
To make things a little nicer, and to make our lives easier too, we will define our input as years since 2004:
Input: \(t\), years since 2004
Output: \(P(t)\), the town’s population
The problem gives us two input-output pairs. Converting them to match our defined variables, the year 2004 would correspond to \(t = 0\), giving the point (0, 6200). Notice that through our clever choice of variable definition, we have “given” ourselves the vertical intercept of the function. The year 2009 would correspond to \(t = 5\), giving the point (5, 8100).
To predict the population in 2013 (\(t = 9\)), we would need an equation for the population. Likewise, to find when the population would reach 15000, we would need to solve for the input that would provide an output of 15000. Either way, we need an equation. To find it, we start by calculating the rate of change:
\[m=\dfrac{8100-6200}{5-0} =\dfrac{1900}{5} =380\text{ people per year}\nonumber \]
Since we already know the vertical intercept of the line, we can immediately write the equation:
\[P(t)=6200+380t\nonumber \]
To predict the population in 2013, we evaluate our function at \(t = 9\)
\[P(9)=6200+380(9)=9620\nonumber \]
If the trend continues, our model predicts a population of 9,620 in 2013.
To find when the population will reach 15,000, we can set \(P(t) = 15000\) and solve for \(t\).
\[\begin{array} {rcl} {15000} &= & { 6200 + 380t} \\ {8800} &= & {380t} \\ {t} &\approx & {23.158} \end{array}\nonumber \]
Our model predicts the population will reach 15,000 in a little more than 23 years after 2004, or somewhere around the year 2027.
Example \(\PageIndex{4}\)
Anna and Emanuel start at the same intersection. Anna walks east at 4 miles per hour while Emanuel walks south at 3 miles per hour. They are communicating with a two-way radio with a range of 2 miles. How long after they start walking will they fall out of radio contact?
Solution
In essence, we can partially answer this question by saying they will fall out of radio contact when they are 2 miles apart, which leads us to ask a new question: how long will it take them to be 2 miles apart?
In this problem, our changing quantities are time and the two peoples’ positions, but ultimately we need to know how long will it take for them to be 2 miles apart. We can see that time will be our input variable, so we’ll define
Input: \(t\), time in hours.
Since it is not obvious how to define our output variables, we’ll start by drawing a picture.
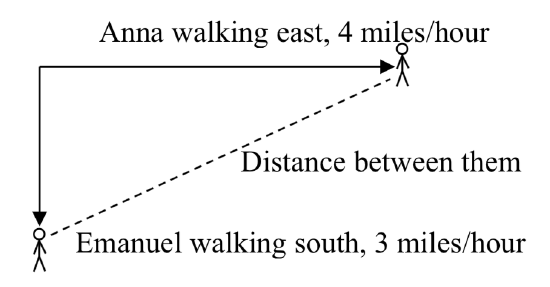
Because of the complexity of this question, it may be helpful to introduce some intermediary variables. These are quantities that we aren’t directly interested in, but seem important to the problem. For this problem, Anna’s and Emanuel’s distances from the starting point seem important. To notate these, we are going to define a coordinate system, putting the “starting point” at the intersection where they both started, then we’re going to introduce a variable, \(A\), to represent Anna’s position, and define it to be a measurement from the starting point, in the eastward direction. Likewise, we’ll introduce a variable, \(E\), to represent Emanuel’s position, measured from the starting point in the southward direction. Note that in defining the coordinate system we specified both the origin, or starting point, of the measurement, as well as the direction of measure.
While we’re at it, we’ll define a third variable, \(D\), to be the measurement of the distance between Anna and Emanuel. Showing the variables on the picture is often helpful:
Looking at the variables on the picture, we remember we need to know how long it takes for \(D\), the distance between them, to equal 2 miles.
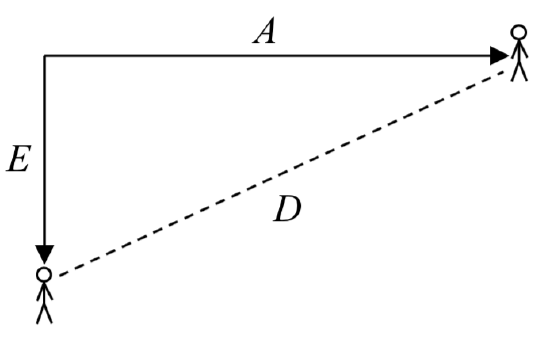
Seeing this picture we remember that in order to find the distance between the two, we can use the Pythagorean Theorem, a property of right triangles.
From here, we can now look back at the problem for relevant information. Anna is walking 4 miles per hour, and Emanuel is walking 3 miles per hour, which are rates of change. Using those, we can write formulas for the distance each has walked.
They both start at the same intersection and so when \(t = 0\), the distance travelled by each person should also be 0, so given the rate for each, and the initial value for each, we get:
\[A(t) = 4t\nonumber \]
\[E(t) = 3t\nonumber \]
Using the Pythagorean theorem we get:
\[D(t)^{2} =A(t)^{2} +E(t)^{2}\nonumber \] substitute in the function formulas
\[D(t)^{2} =(4t)^{2} +(3t)^{2} =16t^{2} +9t^{2} =25t^{2}\nonumber \] solve for \(D(t)\) using the square root
\[D(t)=\pm \sqrt{25t^{2} } =\pm 5|t|\nonumber \]
Since in this scenario we are only considering positive values of t and our distance \(D(t)\) will always be positive, we can simplify this answer to \(D(t)=5t\)
Interestingly, the distance between them is also a linear function. Using it, we can now answer the question of when the distance between them will reach 2 miles:
\[\begin{array} {rcl} {D(t)} &= & {2} \\ {5t} &= & {2} \\ {t} &= & {\dfrac{2}{5} = 0.4} \end{array}\nonumber \]
They will fall out of radio contact in 0.4 hours, or 24 minutes.
Example \(\PageIndex{5}\)
There is currently a straight road leading from the town of Westborough to a town 30 miles east and 10 miles north. Partway down this road, it junctions with a second road, perpendicular to the first, leading to the town of Eastborough. If the town of Eastborough is located 20 miles directly east of the town of Westborough, how far is the road junction from Westborough?
Solution
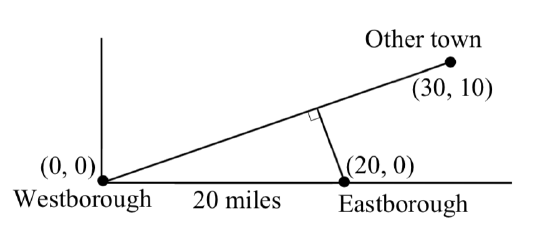 It might help here to draw a picture of the situation. It would then be helpful to introduce a coordinate system. While we could place the origin anywhere, placing it at Westborough seems convenient. This puts the other town at coordinates (30, 10), and Eastborough at (20, 0).
It might help here to draw a picture of the situation. It would then be helpful to introduce a coordinate system. While we could place the origin anywhere, placing it at Westborough seems convenient. This puts the other town at coordinates (30, 10), and Eastborough at (20, 0).
Using this point along with the origin, we can find the slope of the line from Westborough to the other town: \(m=\dfrac{10-0}{30-0} =\dfrac{1}{3}\). This gives the equation of the road from Westborough to the other town to be \(W(x)=\dfrac{1}{3} x\).
From this, we can determine the perpendicular road to Eastborough will have slope \(m=-3\). Since the town of Eastborough is at the point (20, 0), we can find the equation:
\[E(x) = -3x + b\nonumber \] plug in the point (20, 0)
\[0 = -3(20) + b\nonumber \]
\[b = 60\nonumber \]
\[E(x) = -3x + 60\nonumber \]
We can now find the coordinates of the junction of the roads by finding the intersection of these lines. Setting them equal,
\[\dfrac{1}{3} x = -3x + 60\nonumber \]
\[\dfrac{10}{3} x= 60\nonumber \]
\[10x = 180\nonumber \]
\[x = 18\nonumber \] Substituting this back into \(W(x)\)
\[y = W(18) = \dfrac{1}{3} (18) = 6\nonumber \]
The roads intersect at the point (18, 6). Using the distance formula, we can now find the distance from Westborough to the junction:
\[dist=\sqrt{(18-0)^{2} +(6-0)^{2} } \approx 18.934\text{ miles}\nonumber \]
Important Topics of this Section
The problem solving process
- Identify changing quantities, and then carefully and clearly define descriptive variables to represent those quantities. When appropriate, sketch a picture or define a coordinate system.
- Carefully read the problem to identify important information. Look for information giving values for the variables, or values for parts of the functional model, like slope and initial value.
- Carefully read the problem to identify what we are trying to find, identify, solve, or interpret.
- Identify a solution pathway from the provided information to what we are trying to find. Often this will involve checking and tracking units, building a table or even finding a formula for the function being used to model the problem.
- When needed, find a formula for the function.
- Solve or evaluate using the formula you found for the desired quantities.
- Reflect on whether your answer is reasonable for the given situation and whether it makes sense mathematically.
- Clearly convey your result using appropriate units, and answer in full sentences when appropriate.


