3.1E: Power Functions (Exercises)
- Page ID
- 13889
section 3.1 EXERCISE
Find the long run behavior of each function as \(x \to \infty\) and \(x \to -\infty\)
1. \(f(x)=x^{4}\)
2. \(f(x)=x^{6}\)
3. \(f(x)=x^{3}\)
4. \(f(x)=x^{5}\)
5. \(f(x)=-x^{2}\)
6. \(f(x)=-x^{4}\)
7. \(f(x)=-x^{7}\)
8. \(f(x)=-x^{9}\)
Find the degree and leading coefficient of each polynomial
9. \(4x^{7}\)
10. \(5x^{6}\)
11. \(5-x^{2}\)
12. \(6+3x-4x^{3}\)
13. \(-2x^{4} - 3x^{2} + x-1\)
14. \(6x^{5} -2x^{4} + x^{2} + 3\)
15. \((2x+3)(x-4)(3x+1)\)
16. \((3x+1)(x+1)(4x+3)\)
Find the long run behavior of each function as \(x \to \infty\) and \(x \to -\infty\)
17. \(-2x^{4} - 3x^{2} + x-1\)
18. \(6x^{5} -2x^{4} + x^{2} + 3\)
19. \(3x^{2} + x-2\)
20. \(-2x^{3} + x^{2} -x+3\)
21. What is the maximum number of \(x\)-intercepts and turning points for a polynomial of degree 5?
22. What is the maximum number of \(x\)-intercepts and turning points for a polynomial of degree 8?
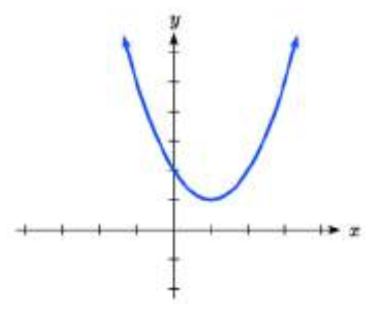
What is the least possible degree of the polynomial function shown in each graph?
23.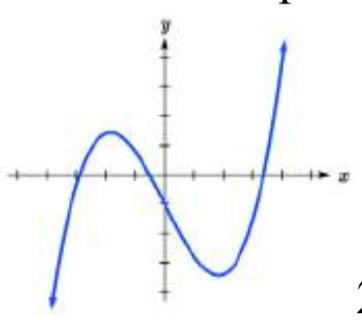 24
24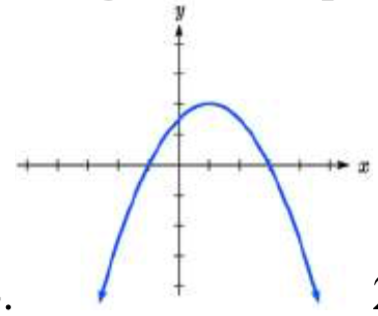 .25.
.25.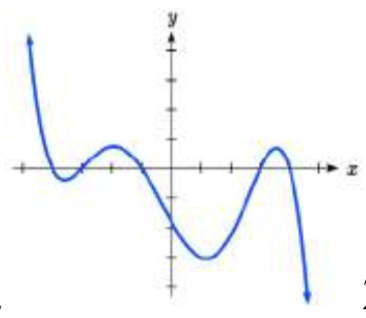 26.
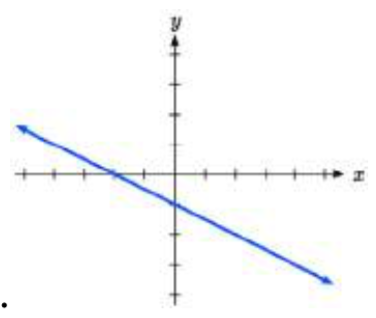
26.
27. 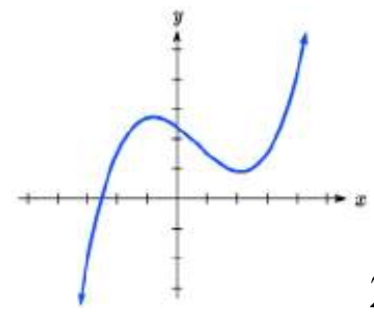 28.
28.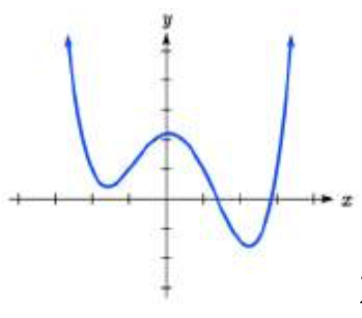 29.
29.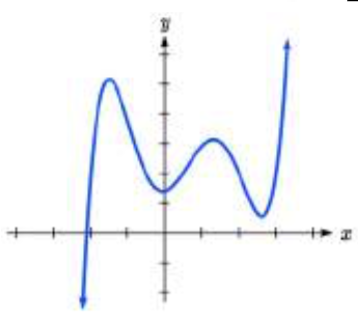 30.
30. 
Find the vertical and horizontal intercepts of each function.
31. \(f(t)=2(t-1)(t+2)(t-3)\)
32. \(f(x)=3(x+1)(x-4)(x+5)\)
33. \(g(n)=-2(3n-1)(2n+1)\)
34. \(k(u)=-3(4-n)(4n+3)\)
- Answer
-
1. As \(x \to \infty\), \(f(x) \to \infty\) As \(x \to -\infty\), \(f(x) \to \infty\)
3. As \(x \to \infty\), \(f(x) \to \infty\) As \(x \to -\infty\), \(f(x) \to -\infty\)
5. As \(x \to \infty\), \(f(x) \to -\infty\) As \(x \to -\infty\), \(f(x) \to -\infty\)
7. As \(x \to \infty\), \(f(x) \to -\infty\) As \(x \to -\infty\), \(f(x) \to \infty\)
9. \(7^{\text{th}}\) Degree, Leading coefficient 4
11. \(2^{\text{nd}}\) Degree, Leading coefficient -1
13. \(4^{\text{th}}\) Degree, Leading coefficient -2
15. \(3^{\text{rd}}\) Degree, Leading coefficient 6
17. As \(x \to \infty\), \(f(x) \to -\infty\) As \(x \to -\infty\), \(f(x) \to -\infty\)
19. As \(x \to \infty\), \(f(x) \to \infty\) As \(x \to -\infty\), \(f(x) \to \infty\)
21. intercepts: 5, turning points: 4
23. 3
25. 5
27. 3
29. 5
31. Horizontal Intercepts (1, 0), (-2, 0), (3, 0) Vertical Intercept (0, 12)
33. Horizontal Intercepts (1/3, 0) (-1/2. 0) Vertical Intercept (0, 2)


