2.2: The Law of Cosines
- Page ID
- 3255
We will now discuss how to solve a triangle in Case 3: two sides and the angle between them. First, let us see what happens when we try to use the Law of Sines for this case.
Solve the triangle \(\triangle\,ABC \) given \(A = 30^\circ \), \(b = 4 \), and \(c = 5 \).

Solution
Using the Law of Sines, we have
\[\nonumber \dfrac{a}{\sin\;30^\circ} ~=~ \dfrac{4}{\sin\;B} ~=~ \dfrac{5}{\sin\;C} ~, \nonumber \]
where each of the equations has two unknown parts, making the problem impossible to solve. For example, to solve for \(a \) we could use the equation
\[\dfrac{4}{\sin\;B} = \dfrac{5}{\sin\;C} \nonumber \]
to solve for \(\sin\;B \) in terms of \(\sin\;C \) and substitute that into the equation
\[\dfrac{a}{\sin\;30^\circ} = \dfrac{4}{\sin\;B}. \nonumber \]
But that would just result in the equation
\[\dfrac{a}{\sin\;30^\circ} = \dfrac{5}{\sin\;C} ,\nonumber \]
which we already knew and which still has two unknowns! Thus, this problem can not be solved using the Law of Sines.
To solve the triangle in the above example, we can use the Law of Cosines:
If a triangle has sides of lengths \(a \), \(b \), and \(c \) opposite the angles \(A \), \(B \), and \(C \), respectively, then
\[\begin{align}
a^2 ~ &= b^2 + c^2 - 2bc\;\cos\;A ~,\label{2.9}\\[4pt]
b^2 ~ &= c^2 + a^2 - 2ca\;\cos\;B ~,\label{2.10}\\[4pt]
c^2 ~ &= a^2 + b^2 - 2ab\;\cos\;C ~.\label{2.11} \\[4pt]
\end{align} \nonumber \]
To prove the Law of Cosines, let \(\triangle\,ABC \) be an oblique triangle. Then \(\triangle\,ABC \) can be acute, as in Figure \(\PageIndex{1a}\), or it can be obtuse, as in Figure \(\PageIndex{1b}\). In each case, draw the altitude from the vertex at \(C \) to the side \(\overline{AB} \). In Figure \(\PageIndex{1a}\), the altitude divides \(\overline{AB} \) into two line segments with lengths \(x \) and \(c-x \), while in Figure \(\PageIndex{1b}\) the altitude extends the side \(\overline{AB} \) by a distance \(x \). Let \(h \) be the height of the altitude.
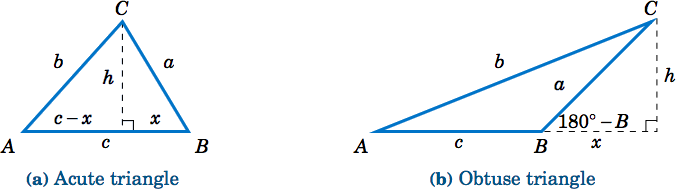
For each triangle in Figure \(\PageIndex{1}\), we see by the Pythagorean Theorem that
\[h^2 ~=~ a^2 ~-~ x^2\label{2.12} \]
and likewise for the acute triangle in Figure \(\PageIndex{1a}\) we see that
\[b^2 ~=~ h^2 ~+~ (c-x)^2 ~.\label{2.13} \]
Thus, substituting the expression for \(h^2 \) in Equation \ref{2.12} into Equation \ref{2.13} gives
\[\begin{align*} b^2 ~&=~ a^2 ~-~ x^2 ~+~ (c-x)^2\nonumber \\
&=~ a^2 ~-~ x^2 ~+~ c^2 ~-~ 2cx ~+~ x^2\nonumber \\
&=~ a^2 ~+~ c^2 ~-~ 2cx ~.\nonumber \\ \end{align*} \nonumber \]
But we see from Figure \(\PageIndex{1a}\) that \(x = a\;\cos\;B \), so
\[ b^2 ~=~ a^2 ~+~ c^2 ~-~ 2ca\;\cos\;B ~.\label{2.14} \]
And for the obtuse triangle in Figure \(\PageIndex{1b}\) we see that
\[ b^2 ~=~ h^2 ~+~ (c+x)^2 ~.\label{2.15} \]
Thus, substituting the expression for \(h^2 \) in Equation \ref{2.12} into Equation \ref{2.15} gives
\[ \begin{align*}b^2 ~&=~ a^2 ~-~ x^2 ~+~ (c+x)^2\nonumber \\
&=~ a^2 ~-~ x^2 ~+~ c^2 ~+~ 2cx ~+~ x^2\nonumber \\
&=~ a^2 ~+~ c^2 ~+~ 2cx ~.\nonumber \\ \end{align*} \nonumber \]
But we see from Figure \(\PageIndex{1a}\) that \(x = a\;\cos\;(180^\circ - B) \), and we know from Section 1.5 that \(\cos\;(180^\circ - B) = -\cos\;B \). Thus, \(x = -a\;\cos\;B\) and so
\[ b^2 ~=~ a^2 ~+~ c^2 ~-~ 2ca\;\cos\;B ~.\label{2.16} \]
So for both acute and obtuse triangles we have proved Equation \ref{2.10} in the Law of Cosines. Notice that the proof was for \(B \) acute and obtuse. By similar arguments for \(A \) and \(C\) we get the other two formulas.
\(\square\)
Note that we did not prove the Law of Cosines for right triangles, since it turns out (see Exercise 15) that all three formulas reduce to the Pythagorean Theorem for that case. The Law of Cosines can be viewed as a generalization of the Pythagorean Theorem.
Also, notice that it suffices to remember just one of the three Equations \ref{2.9}-\ref{2.11}, since the other two can be obtained by "cycling'' through the letters \(a \), \(b \), and \(c \). That is, replace \(a \) by \(b \), replace \(b \) by \(c \), and replace \(c \) by \(a \) (likewise for the capital letters). One cycle will give you the second formula, and another cycle will give you the third.
The angle between two sides of a triangle is often called the included angle. Notice in the Law of Cosines that if two sides and their included angle are known (e.g. \(b \), \(c \), and \(A\)), then we have a formula for the square of the third side. We will now solve the triangle from Example \(\PageIndex{2}\).
Solve the triangle \(\triangle\,ABC \) given \(A = 30^\circ \), \(b = 4 \), and \(c = 5 \).
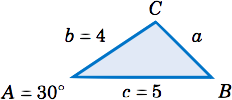
Solution
We will use the Law of Cosines to find \(a \), use it again to find \(B \), then use \(C = 180^\circ - A - B \). First, we have
\[\nonumber \begin{align*}
a^2 ~ &= ~ b^2 ~ &+ ~ c^2 ~ &- ~ 2bc\;\cos\;A\\ \nonumber
&= ~ 4^2 ~ &+ ~ 5^2 ~ &- ~ 2(4)(5)\;\cos\;30^\circ ~=~ 6.36 \quad\Rightarrow\quad
\boxed{a ~=~ 2.52} ~.\\
\end{align*} \nonumber \]
Now we use the formula for \(b^2 \) to find \(B\):
\[\nonumber \begin{align*}
b^2 ~ = ~ c^2 ~ + ~ a^2 ~ - ~ 2ca\;\cos\;B \quad&\Rightarrow\quad
\cos\;B ~=~ \dfrac{c^2 ~ + ~ a^2 ~-~ b^2}{2ca}\\ \nonumber
&\Rightarrow\quad \cos\;B ~=~ \dfrac{5^2 ~ + ~ (2.52)^2 ~-~ 4^2}{2(5)(2.52)} ~=~ 0.6091\\ \nonumber
&\Rightarrow\quad \boxed{B ~=~ 52.5^\circ}\\
\end{align*} \nonumber \]
Thus, \(C = 180^\circ - A - B = 180^\circ - 30^\circ - 52.5^\circ \Rightarrow \fbox{\(C = 97.5^\circ \; \)}\).
Notice in Example \(\PageIndex{2}\) that there was only one solution. For Case 3 this will always be true: when given two sides and their included angle, the triangle will have exactly one solution. The reason is simple: when joining two line segments at a common vertex to form an angle, there is exactly one way to connect their free endpoints with a third line segment, regardless of the size of the angle.
You may be wondering why we used the Law of Cosines a second time in Example \(\PageIndex{2}\), to find the angle \(B \). Why not use the Law of Sines, which has a simpler formula? The reason is that using the cosine function eliminates any ambiguity: if the cosine is positive then the angle is acute, and if the cosine is negative then the angle is obtuse. This is in contrast to using the sine function; as we saw in Section 2.1, both an acute angle and its obtuse supplement have the same positive sine.
To see this, suppose that we had used the Law of Sines to find \(B \) in Example \(\PageIndex{2}\):
\[ \sin\;B ~=~ \dfrac{b\;\sin\;A}{a} ~=~ \dfrac{4\;\sin\;30^\circ}{2.52} ~=~ 0.7937
\quad\Rightarrow\quad B ~=~ 52.5^\circ ~\text{or}~ 127.5^\circ
\nonumber \]
How would we know which answer is correct? We could not immediately rule out \(B = 127.5^\circ \) as too large, since it would make \(A + B = 157.5^\circ < 180^\circ \) and so \(C = 22.5^\circ \), which seems like it could be a valid solution. However, this solution is impossible. Why? Because the largest side in the triangle is \(c = 5 \), which (as we learned in Section 2.1) means that \(C \) has to be the largest angle. But \(C = 22.5^\circ \) would not be the largest angle in this solution, and hence we have a contradiction.
It remains to solve a triangle in Case 4, i.e. given three sides. We will now see how to use the Law of Cosines for that case.
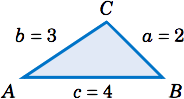
Solve the triangle \(\triangle\,ABC \) given \(a = 2 \), \(b = 3 \), and \(c = 4 \).
Solution
We will use the Law of Cosines to find \(B \) and \(C \), then use \(A = 180^\circ - B - C \). First, we use the formula for \(b^2 \) to find \(B\):
\[\nonumber \begin{align*}
b^2 ~ = ~ c^2 ~ + ~ a^2 ~ - ~ 2ca\;\cos\;B \quad&\Rightarrow\quad
\cos\;B ~=~ \dfrac{c^2 ~ + ~ a^2 ~-~ b^2}{2ca}\\ \nonumber
&\Rightarrow\quad \cos\;B ~=~ \dfrac{4^2 ~ + ~ 2^2 ~-~ 3^2}{2(4)(2)} ~=~ 0.6875\\ \nonumber
&\Rightarrow\quad \boxed{B ~=~ 46.6^\circ} \\
\end{align*} \nonumber \]
Now we use the formula for \(c^2 \) to find \(C\):
\[\nonumber \begin{align*}
c^2 ~ = ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\cos\;C \quad&\Rightarrow\quad
\cos\;C ~=~ \dfrac{a^2 ~ + ~ b^2 ~-~ c^2}{2ab}\\ \nonumber
&\Rightarrow\quad \cos\;C ~=~ \dfrac{2^2 ~ + ~ 3^2 ~-~ 4^2}{2(2)(3)} ~=~ -0.25\\ \nonumber
&\Rightarrow\quad \boxed{C ~=~ 104.5^\circ} \\
\end{align*} \nonumber \]
Thus, \(A = 180^\circ - B - C = 180^\circ - 46.6^\circ - 104.5^\circ \Rightarrow \boxed{A = 28.9^\circ}\; \).
It may seem that there is always a solution in Case 4 (given all three sides), but that is not true, as the following example shows.
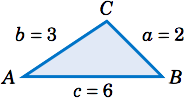
Solve the triangle \(\triangle\,ABC \) given \(a = 2 \), \(b = 3 \), and \(c = 6 \).
Solution
If we blindly try to use the Law of Cosines to find \(A \), we get
\[ a^2 ~ = ~ b^2 ~ + ~ c^2 ~ - ~ 2bc\;\cos\;A \quad\Rightarrow\quad \cos\;A ~=~
\dfrac{b^2 ~ + ~ c^2 ~-~ a^2}{2bc} ~=~ \dfrac{3^2 ~ + ~ 6^2 ~-~ 2^2}{2(3)(6)} ~=~ 1.139 ~,
\nonumber \]
which is impossible since \(| \cos\;A | \le 1 \). Thus, there is \(\fbox{no solution}\).
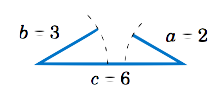
We could have saved ourselves some effort by recognizing that the length of one of the sides (\(c=6\)) is greater than the sums of the lengths of the remaining sides (\(a=2 \) and \(b=3\)), which (as the picture below shows) is impossible in a triangle.
The Law of Cosines can also be used to solve triangles in Case 2 (two sides and one opposite angle), though it is less commonly used for that purpose than the Law of Sines. The following example gives an idea of how to do this.
Solve the triangle \(\triangle\,ABC \) given \(a = 18 \), \(A = 25^\circ \), and \(b = 30 \).
Solution
In Example 2.2 from Section 2.1 we used the Law of Sines to show that there are two sets of solutions for this triangle: \(B = 44.8^\circ \), \(C = 110.2^\circ \), \(c = 40 \) and \(B = 135.2^\circ \), \(C = 19.8^\circ \), \(c = 14.4 \). To solve this using the Law of Cosines, first find \(c \) by using the formula for \(a^2\):
\[ \nonumber \begin{align*}
a^2 ~ = ~ b^2 ~ + ~ c^2 ~ - ~ 2bc\;\cos\;A \quad&\Rightarrow\quad
18^2 = ~ 30^2 ~ + ~ c^2 ~ - ~ 2(30)c\;\cos\;25^\circ\\ \nonumber
&\Rightarrow\quad c^2 ~-~ 54.38\,c ~+~ 576 ~ = ~ 0 ~,
\end{align*} \nonumber \]
which is a quadratic equation in \(c \), so we know that it can have either zero, one, or two real roots (corresponding to the number of solutions in Case 2). By the quadratic formula, we have
\[ c ~=~ \dfrac{54.38 ~\pm~ \sqrt{(54.38)^2 ~-~ 4(1)(576)}}{2(1)} ~=~ 40 ~~\text{or}~~ 14.4 ~.
\nonumber \]
Note that these are the same values for \(c \) that we found before. For \(c=40 \) we get
\[ \cos\;B ~=~ \dfrac{c^2 ~ + ~ a^2 ~-~ b^2}{2ca} ~=~
\dfrac{40^2 ~ + ~ 18^2 ~-~ 30^2}{2(40)(18)} ~=~ 0.7111
\quad\Rightarrow\quad B ~=~ 44.7^\circ \quad\Rightarrow\quad C ~=~ 110.3^\circ ~,
\nonumber \]
which is close to what we found before (the small difference being due to different rounding). The other solution set can be obtained similarly.
Like the Law of Sines, the Law of Cosines can be used to prove some geometric facts, as in the following example.
Use the Law of Cosines to prove that the sum of the squares of the diagonals of any parallelogram equals the sum of the squares of the sides.
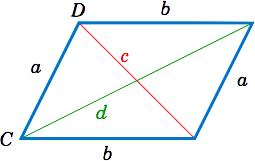
Solution:
Let \(a \) and \(b \) be the lengths of the sides, and let the diagonals opposite the angles \(C \) and \(D \) have lengths \(c \) and \(d \), respectively, as in Figure \(\PageIndex{2}\). Then we need to show that
\[c^2 ~+~ d^2 ~=~ a^2 ~+~ b^2 ~+~ a^2 ~+~ b^2 ~=~ 2\,( a^2 ~+~ b^2 ) ~.\nonumber \]
By the Law of Cosines, we know that
\[\nonumber \begin{align*}
c^2 ~ &= ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\cos\;C ~,~\text{and}\\ \nonumber
d^2 ~ &= ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\cos\;D ~. \\ \end{align*} \nonumber \]
By properties of parallelograms, we know that \(D = 180^\circ - C \), so
\[\nonumber \begin{align*} d^2 ~ &= ~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\cos\;(180^\circ - C)\\ \nonumber &=~ a^2 ~ + ~ b^2 ~ + ~ 2ab\;\cos\;C ~, \\ \end{align*} \nonumber \]
since \(\;\cos\;(180^\circ - C) = -\cos\;C \). Thus,
\[\nonumber \begin{align*} c^2 ~+~ d^2 ~&=~ a^2 ~ + ~ b^2 ~ - ~ 2ab\;\cos\;C ~+~ a^2 ~ + ~ b^2 ~ + ~ 2ab\;\cos\;C\\ \nonumber
&=~ 2\,( a^2 ~+~ b^2 ) ~. \quad \\ \end{align*} \nonumber \]


