8.5: Polar Form of Complex Numbers
- Last updated
- Save as PDF
- Page ID
- 1379
Learning Objectives
- Plot complex numbers in the complex plane.
- Find the absolute value of a complex number.
- Write complex numbers in polar form.
- Convert a complex number from polar to rectangular form.
- Find products of complex numbers in polar form.
- Find quotients of complex numbers in polar form.
- Find powers of complex numbers in polar form.
- Find roots of complex numbers in polar form.
“God made the integers; all else is the work of man.” This rather famous quote by nineteenth-century German mathematician Leopold Kronecker sets the stage for this section on the polar form of a complex number. Complex numbers were invented by people and represent over a thousand years of continuous investigation and struggle by mathematicians such as Pythagoras, Descartes, De Moivre, Euler, Gauss, and others. Complex numbers answered questions that for centuries had puzzled the greatest minds in science.
We first encountered complex numbers in the section on Complex Numbers. In this section, we will focus on the mechanics of working with complex numbers: translation of complex numbers from polar form to rectangular form and vice versa, interpretation of complex numbers in the scheme of applications, and application of De Moivre’s Theorem.
Plotting Complex Numbers in the Complex Plane
Plotting a complex number \(a+bi\) is similar to plotting a real number, except that the horizontal axis represents the real part of the number, \(a\), and the vertical axis represents the imaginary part of the number, \(bi\).
How to: Given a complex number \(a+bi\), plot it in the complex plane.
- Label the horizontal axis as the real axis and the vertical axis as the imaginary axis.
- Plot the point in the complex plane by moving \(a\) units in the horizontal direction and \(b\) units in the vertical direction.
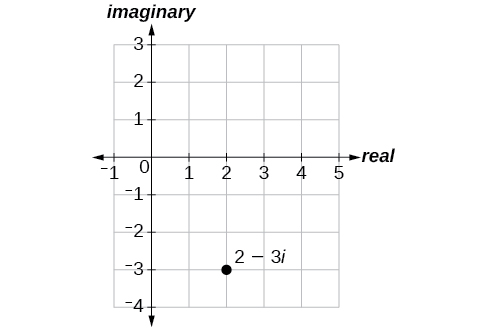
Example \(\PageIndex{1}\): Plotting a Complex Number in the Complex Plane
Plot the complex number \(2−3i\) in the complex plane.
Solution
From the origin, move two units in the positive horizontal direction and three units in the negative vertical direction. See Figure \(\PageIndex{1}\).
Exercise \(\PageIndex{1}\)
Plot the point \(1+5i\) in the complex plane.
- Answer
-
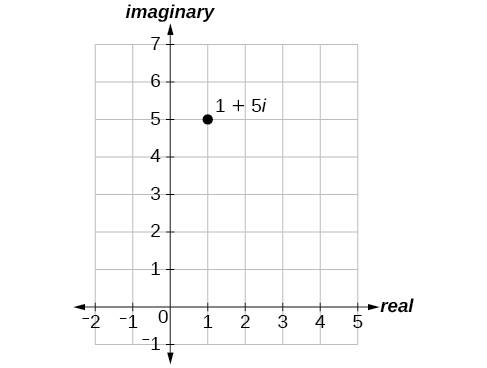
Figure \(\PageIndex{2}\)
Finding the Absolute Value of a Complex Number
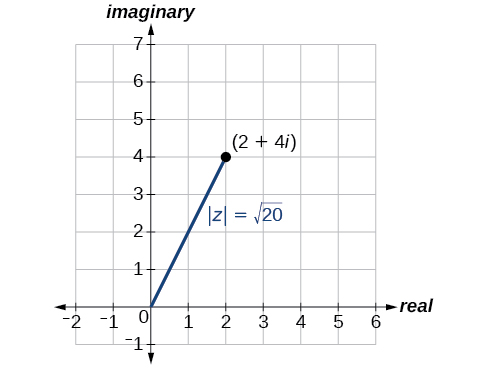
The first step toward working with a complex number in polar form is to find the absolute value. The absolute value of a complex number is the same as its magnitude, or \(| z |\). It measures the distance from the origin to a point in the plane. For example, the graph of \(z=2+4i\), in Figure \(\PageIndex{3}\), shows \(| z |\).
ABSOLUTE VALUE OF A COMPLEX NUMBER
Given \(z=x+yi\), a complex number, the absolute value of \(z\) is defined as
\[| z |=\sqrt{x^2+y^2}\]
It is the distance from the origin to the point \((x,y)\).
Notice that the absolute value of a real number gives the distance of the number from \(0\), while the absolute value of a complex number gives the distance of the number from the origin, \((0, 0)\).
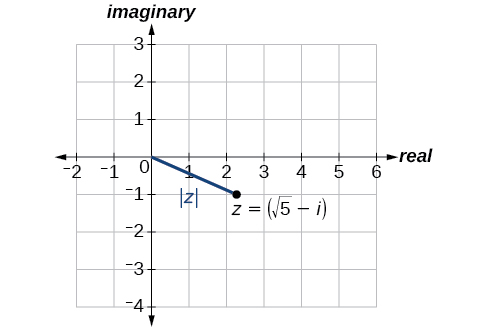
Example \(\PageIndex{2}\): Finding the Absolute Value of a Complex Number with a Radical
Find the absolute value of \(z=\sqrt{5}−i\).
Solution
Using the formula, we have
\[\begin{align*} |z| &= \sqrt{x^2+y^2} \\ |z| &= \sqrt{{(\sqrt{5})}^2+{(-1)}^2} \\ |z| &= \sqrt{5+1} \\ |z| &= \sqrt{6} \end{align*}\]
See Figure \(\PageIndex{4}\).
Exercise \(\PageIndex{2}\)
Find the absolute value of the complex number \(z=12−5i\).
- Answer
-
\(13\)
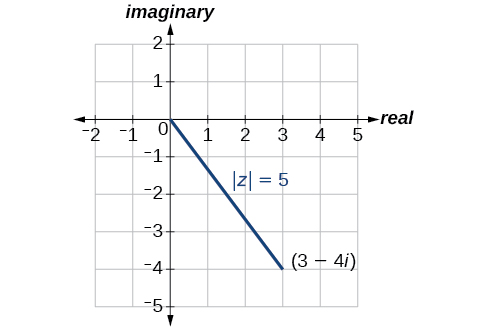
Example \(\PageIndex{3}\): Finding the Absolute Value of a Complex Number
Given \(z=3−4i\), find \(| z |\).
Solution
Using the formula, we have
\[\begin{align*} | z | &= \sqrt{x^2+y^2} \\ | z | &= \sqrt{{(3)}^2+{(-4)}^2} \\ | z | &= \sqrt{9+16} \\ | z | &= \sqrt{25} \\ | z | &= 5 \end{align*}\]
The absolute value \(z\) is \(5\). See Figure \(\PageIndex{5}\).
Exercise \(\PageIndex{3}\)
Given \(z=1−7i\), find \(| z |\).
- Answer
-
\(| z |=\sqrt{50}=5\sqrt{2}\)
Writing Complex Numbers in Polar Form
The polar form of a complex number expresses a number in terms of an angle \(\theta\) and its distance from the origin \(r\). Given a complex number in rectangular form expressed as \(z=x+yi\), we use the same conversion formulas as we do to write the number in trigonometric form:
\[\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align*}\]
We review these relationships in Figure \(\PageIndex{6}\).
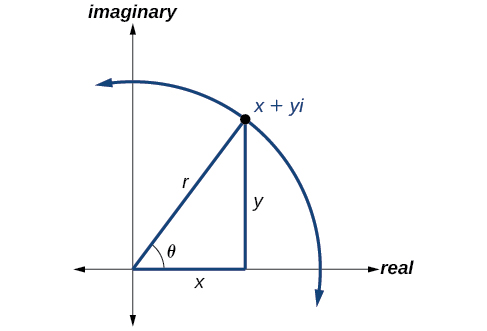
We use the term modulus to represent the absolute value of a complex number, or the distance from the origin to the point \((x,y)\). The modulus, then, is the same as \(r\), the radius in polar form. We use \(\theta\) to indicate the angle of direction (just as with polar coordinates). Substituting, we have
\[\begin{align*} z &= x+yi \\ z &= r \cos \theta+(r \sin \theta)i \\ z &= r(\cos \theta+i \sin \theta) \end{align*}\]
POLAR FORM OF A COMPLEX NUMBER
Writing a complex number in polar form involves the following conversion formulas:
\[\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align}\]
Making a direct substitution, we have
\[\begin{align} z &= x+yi \\ z &= (r \cos \theta)+i(r \sin \theta) \\ z &= r(\cos \theta+i \sin \theta) \end{align}\]
where \(r\) is the modulus and \(\theta\) is the argument. We often use the abbreviation \(r\; cis \theta\) to represent \(r(\cos \theta+i \sin \theta)\).
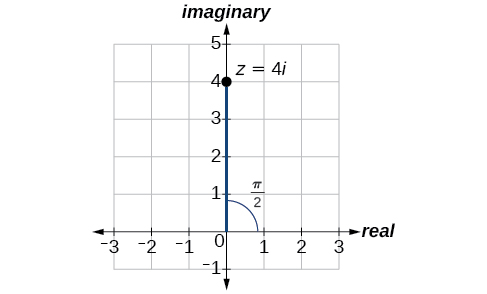
Example \(\PageIndex{4}\): Expressing a Complex Number Using Polar Coordinates
Express the complex number \(4i\) using polar coordinates.
Solution
On the complex plane, the number \(z=4i\) is the same as \(z=0+4i\). Writing it in polar form, we have to calculate \(r\) first.
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{0^2+4^2} \\ r &= \sqrt{16} \\ r &= 4 \end{align*}\]
Next, we look at \(x\). If \(x=r \cos \theta\), and \(x=0\), then \(\theta=\dfrac{\pi}{2}\). In polar coordinates, the complex number \(z=0+4i\) can be written as \(z=4\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right) \text{ or } 4\; cis\left( \dfrac{\pi}{2}\right)\). See Figure \(\PageIndex{7}\).
Exercise \(\PageIndex{4}\)
Express \(z=3i\) as \(r\space cis \theta\) in polar form.
- Answer
-
\(z=3\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right)\)
Example \(\PageIndex{5}\): Finding the Polar Form of a Complex Number
Find the polar form of \(−4+4i\).
Solution
First, find the value of \(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(−4)}^2+(4^2)} \\ r &= \sqrt{32} \\ r &= 4\sqrt{2} \end{align*}\]
Find the angle \(\theta\) using the formula:
\[\begin{align*} \cos \theta &= \dfrac{x}{r} \\ \cos \theta &= \dfrac{−4}{4\sqrt{2}} \\ \cos \theta &= −\dfrac{1}{\sqrt{2}} \\ \theta &= {\cos}^{−1} \left(−\dfrac{1}{\sqrt{2}}\right)\\ &= \dfrac{3\pi}{4} \end{align*}\]
Thus, the solution is \(4\sqrt{2}\space cis \left(\dfrac{3\pi}{4}\right)\).
Exercise \(\PageIndex{5}\)
Write \(z=\sqrt{3}+i\) in polar form.
- Answer
-
\(z=2\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Converting a Complex Number from Polar to Rectangular Form
Converting a complex number from polar form to rectangular form is a matter of evaluating what is given and using the distributive property. In other words, given \(z=r(\cos \theta+i \sin \theta)\), first evaluate the trigonometric functions \(\cos \theta\) and \(\sin \theta\). Then, multiply through by \(r\).
Example \(\PageIndex{6A}\): Converting from Polar to Rectangular Form
Convert the polar form of the given complex number to rectangular form:
\(z=12\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Solution
We begin by evaluating the trigonometric expressions.
\[\begin{align*} \cos\left(\dfrac{\pi}{6}\right)&= \dfrac{\sqrt{3}}{2} \text{ and } \sin(\dfrac{\pi}{6})=\dfrac{1}{2}\\ \text {After substitution, the complex number is}\\ z&= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \end{align*}\]
We apply the distributive property:
\[\begin{align*} z &= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\ &= (12)\dfrac{\sqrt{3}}{2}+(12)\dfrac{1}{2}i \\ &= 6\sqrt{3}+6i \end{align*}\]
The rectangular form of the given point in complex form is \(6\sqrt{3}+6i\).
Example \(\PageIndex{6B}\): Finding the Rectangular Form of a Complex Number
Find the rectangular form of the complex number given \(r=13\) and \(\tan \theta=\dfrac{5}{12}\).
Solution
If \(\tan \theta=\dfrac{5}{12}\), and \(\tan \theta=\dfrac{y}{x}\), we first determine \(r=\sqrt{x^2+y^2}=\sqrt{122+52}=13\). We then find \(\cos \theta=\dfrac{x}{r}\) and \(\sin \theta=\dfrac{y}{r}\).
\[\begin{align*} z &= 13\left(\cos \theta+i \sin \theta\right) \\ &= 13\left(\dfrac{12}{13}+\dfrac{5}{13}i\right) \\ &=12+5i \end{align*}\]
The rectangular form of the given number in complex form is \(12+5i\).
Exercise \(\PageIndex{6}\)
Convert the complex number to rectangular form:
\(z=4\left(\cos \dfrac{11\pi}{6}+i \sin \dfrac{11\pi}{6}\right)\)
- Answer
-
\(z=2\sqrt{3}−2i\)
Finding Products of Complex Numbers in Polar Form
Now that we can convert complex numbers to polar form we will learn how to perform operations on complex numbers in polar form. For the rest of this section, we will work with formulas developed by French mathematician Abraham de Moivre (1667-1754). These formulas have made working with products, quotients, powers, and roots of complex numbers much simpler than they appear. The rules are based on multiplying the moduli and adding the arguments.
PRODUCTS OF COMPLEX NUMBERS IN POLAR FORM
If \(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) and \(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), then the product of these numbers is given as:
\[\begin{align} z_1z_2 &= r_1r_2[ \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2) ] \\ z_1z_2 &= r_1r_2\space cis(\theta_1+\theta_2) \end{align}\]
Notice that the product calls for multiplying the moduli and adding the angles.
Example \(\PageIndex{7}\): Finding the Product of Two Complex Numbers in Polar Form
Find the product of \(z_1z_2\), given \(z_1=4(\cos(80°)+i \sin(80°))\) and \(z_2=2(\cos(145°)+i \sin(145°))\).
Solution
Follow the formula
\[\begin{align*} z_1z_2 &= 4⋅2[\cos(80°+145°)+i \sin(80°+145°)] \\ z_1z_2 &= 8[\cos(225°)+i \sin(225°)] \\ z_1z_2 &= 8\left[\cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ z_1z_2 &= 8\left[−\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ z_1z_2 &= −4\sqrt{2}−4i\sqrt{2} \end{align*}\]
Finding Quotients of Complex Numbers in Polar Form
The quotient of two complex numbers in polar form is the quotient of the two moduli and the difference of the two arguments.
QUOTIENTS OF COMPLEX NUMBERS IN POLAR FORM
If \(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) and \(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), then the quotient of these numbers is
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}[\cos(\theta_1−\theta_2)+i \sin(\theta_1−\theta_2) ],\space z_2≠0\]
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\space cis(\theta_1−\theta_2),\space z_2≠0\]
Notice that the moduli are divided, and the angles are subtracted.
How to: Given two complex numbers in polar form, find the quotient
- Divide \(\dfrac{r_1}{r_2}\).
- Find \(\theta_1−\theta_2\).
- Substitute the results into the formula: \(z=r(\cos \theta+i \sin \theta)\). Replace \(r\) with \(\dfrac{r_1}{r_2}\), and replace \(\theta\) with \(\theta_1−\theta_2\).
- Calculate the new trigonometric expressions and multiply through by \(r\).
Example \(\PageIndex{8}\): Finding the Quotient of Two Complex Numbers
Find the quotient of \(z_1=2(\cos(213°)+i \sin(213°))\) and \(z_2=4(\cos(33°)+i \sin(33°))\).
Solution
Using the formula, we have
\[\begin{align*} \dfrac{z_1}{z_2} &= \dfrac{2}{4}[\cos(213°−33°)+i \sin(213°−33°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[\cos(180°)+i \sin(180°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[−1+0i] \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2}+0i \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2} \end{align*}\]
Exercise \(\PageIndex{8}\)
Find the product and the quotient of \(z_1=2\sqrt{3}(\cos(150°)+i \sin(150°))\) and \(z_2=2(\cos(30°)+i \sin(30°))\).
- Answer
-
\(z_1z_2=−4\sqrt{3}\); \(\dfrac{z_1}{z_2}=−\dfrac{\sqrt{3}}{2}+\dfrac{3}{2}i\)
Finding Powers of Complex Numbers in Polar Form
Finding powers of complex numbers is greatly simplified using De Moivre’s Theorem. It states that, for a positive integer \(n\), \(z^n\) is found by raising the modulus to the \(n^{th}\) power and multiplying the argument by \(n\). It is the standard method used in modern mathematics.
DE MOIVRE’S THEOREM
If \(z=r(\cos \theta+i \sin \theta)\) is a complex number, then
\[\begin{align} z^n &= r^n[\cos(n\theta)+i \sin(n\theta) ] \\ z^n &= r^n\space cis(n\theta) \end{align}\]
where \(n\) is a positive integer.
Example \(\PageIndex{9}\): Evaluating an Expression Using De Moivre’s Theorem
Evaluate the expression \({(1+i)}^5\) using De Moivre’s Theorem.
Solution
Since De Moivre’s Theorem applies to complex numbers written in polar form, we must first write \((1+i)\) in polar form. Let us find \(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(1)}^2+{(1)}^2} \\ r &= \sqrt{2} \end{align*}\]
Then we find \(\theta\). Using the formula \(\tan \theta=\dfrac{y}{x}\) gives
\[\begin{align*} \tan \theta &= \dfrac{1}{1} \\ \tan \theta &= 1 \\ \theta &= \dfrac{\pi}{4} \end{align*}\]
Use De Moivre’s Theorem to evaluate the expression.
\[\begin{align*} {(a+bi)}^n &= r^n[\cos(n\theta)+i \sin(n\theta)] \\ {(1+i)}^5 &= {(\sqrt{2})}^5\left[ \cos\left(5⋅\dfrac{\pi}{4}\right)+i \sin\left(5⋅\dfrac{\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ \cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ −\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ {(1+i)}^5 &= −4−4i \end{align*}\]
Finding Roots of Complex Numbers in Polar Form
To find the \(n^{th}\) root of a complex number in polar form, we use the \(n^{th}\) Root Theorem or De Moivre’s Theorem and raise the complex number to a power with a rational exponent. There are several ways to represent a formula for finding \(n^{th}\) roots of complex numbers in polar form.
THE \(N^{TH}\) ROOT THEOREM
To find the \(n^{th}\) root of a complex number in polar form, use the formula given as
\[z^{\tfrac{1}{n}}=r^{\tfrac{1}{n}}\left[ \cos\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right)+i \sin\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right) \right]\]
where \(k=0, 1, 2, 3, . . . , n−1\). We add \(\dfrac{2k\pi}{n}\) to \(\dfrac{\theta}{n}\) in order to obtain the periodic roots.
th Root of a Complex Number
Evaluate the cube roots of \(z=8\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)\).
Solution
We have
\[\begin{align*} z^{\frac{1}{3}} &= 8^{\frac{1}{3}}\left[ \cos\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right) \right] \\ z^{\frac{1}{3}} &= 2\left[ \cos\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right) \right] \end{align*}\]
There will be three roots: \(k=0, 1, 2\). When \(k=0\), we have
\(z^{\frac{1}{3}}=2\left(\cos\left(\dfrac{2\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}\right)\right)\)
When \(k=1\), we have
\[\begin{align*} z^{\frac{1}{3}} &=2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right) \right] \;\;\;\;\;\;\;\;\; \text{Add }\dfrac{2(1)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{8\pi}{9}\right)+i \sin\left(\dfrac{8\pi}{9}\right)\right) \end{align*}\]
When \(k=2\), we have
\[\begin{align*} z^{\frac{1}{3}} &= 2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right) \right] \;\;\;\;\;\;\; \text{Add }\dfrac{2(2)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{14\pi}{9}\right)+i \sin\left(\dfrac{14\pi}{9}\right)\right) \end{align*}\]
Remember to find the common denominator to simplify fractions in situations like this one. For \(k=1\), the angle simplification is
\[\begin{align*} \dfrac{\dfrac{2\pi}{3}}{3}+\dfrac{2(1)\pi}{3} &= \dfrac{2\pi}{3}(\dfrac{1}{3})+\dfrac{2(1)\pi}{3}\left(\dfrac{3}{3}\right) \\ &=\dfrac{2\pi}{9}+\dfrac{6\pi}{9} \\ &=\dfrac{8\pi}{9} \end{align*}\]
Exercise \(\PageIndex{10}\)
Find the four fourth roots of \(16(\cos(120°)+i \sin(120°))\).
- Answer
-
\(z_0=2(\cos(30°)+i \sin(30°))\)
\(z_1=2(\cos(120°)+i \sin(120°))\)
\(z_2=2(\cos(210°)+i \sin(210°))\)
\(z_3=2(\cos(300°)+i \sin(300°))\)
Media
Access these online resources for additional instruction and practice with polar forms of complex numbers.
- The Product and Quotient of Complex Numbers in Trigonometric Form
- De Moivre’s Theorem
Key Concepts
- Complex numbers in the form \(a+bi\) are plotted in the complex plane similar to the way rectangular coordinates are plotted in the rectangular plane. Label the \(x\)-axis as the real axis and the \(y\)-axis as the imaginary axis. See Example \(\PageIndex{1}\).
- The absolute value of a complex number is the same as its magnitude. It is the distance from the origin to the point: \(| z |=\sqrt{a^2+b^2}\). See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
- To write complex numbers in polar form, we use the formulas \(x=r \cos \theta\), \(y=r \sin \theta\), and \(r=\sqrt{x^2+y^2}\). Then, \(z=r(\cos \theta+i \sin \theta)\). See Example \(\PageIndex{4}\) and Example \(\PageIndex{5}\).
- To convert from polar form to rectangular form, first evaluate the trigonometric functions. Then, multiply through by \(r\). See Example \(\PageIndex{6}\) and Example \(\PageIndex{7}\).
- To find the product of two complex numbers, multiply the two moduli and add the two angles. Evaluate the trigonometric functions, and multiply using the distributive property. See Example \(\PageIndex{8}\).
- To find the quotient of two complex numbers in polar form, find the quotient of the two moduli and the difference of the two angles. See Example \(\PageIndex{9}\).
- To find the power of a complex number \(z^n\), raise \(r\) to the power \(n\), and multiply \(\theta\) by \(n\). See Example \(\PageIndex{10}\).
- Finding the roots of a complex number is the same as raising a complex number to a power, but using a rational exponent. See Example \(\PageIndex{11}\).


