3.1: Basic Trigonometric Identities
- Page ID
- 3285
So far we know a few relations between the trigonometric functions. For example, we know the reciprocal relations:
- \(\csc\;\theta ~=~ \dfrac{1}{\sin\;\theta} \qquad \) when \(\sin\;\theta \ne 0\)
- \(\sec\;\theta ~=~ \dfrac{1}{\cos\;\theta} \qquad \) when \(\cos\;\theta \ne 0\)
- \(\cot\;\theta ~=~ \dfrac{1}{\tan\;\theta} \qquad \) when \(\tan\;\theta \) is defined and not \(0\)
- \(\sin\;\theta ~=~ \dfrac{1}{\csc\;\theta} \qquad \) when \(\csc\;\theta \) is defined and not \(0\)
- \(\cos\;\theta ~=~ \dfrac{1}{\sec\;\theta} \qquad \) when \(\sec\;\theta \) is defined and not \(0\)
- \(\tan\;\theta ~=~ \dfrac{1}{\cot\;\theta} \qquad \) when \(\cot\;\theta \) is defined and not \(0\)
Notice that each of these equations is true for all angles \(\theta \) for which both sides of the equation are defined. Such equations are called identities, and in this section we will discuss several trigonometric identities, i.e. identities involving the trigonometric functions. These identities are often used to simplify complicated expressions or equations. For example, one of the most useful trigonometric identities is the following:
\[ \tan\;\theta ~=~ \frac{\sin\;\theta}{\cos\;\theta} \qquad \text{when } \cos\;\theta \ne 0 \label{3.1} \]
To prove this identity, pick a point \((x,y) \) on the terminal side of \(\theta \) a distance \(r >0 \) from the origin, and suppose that \(\cos\;\theta \ne 0 \). Then \(x \ne 0 \) (since \(\cos\;\theta = \frac{x}{r}\)), so by definition
\[ \frac{\sin\;\theta}{\cos\;\theta} ~=~ \dfrac{~\dfrac{y}{r}~}{~\dfrac{x}{r}~} ~=~ \frac{y}{x} ~=~
\tan\;\theta ~.
\nonumber \]
Note how we proved the identity by expanding one of its sides (\(\frac{\sin\;\theta}{\cos\;\theta}\)) until we got an expression that was equal to the other side (\(\tan\;\theta\)). This is probably the most common technique for proving identities. Taking reciprocals in the above identity gives:
\[ \cot\;\theta ~=~ \frac{\cos\;\theta}{\sin\;\theta} \qquad \text{when } \sin\;\theta \ne 0 \label{3.2} \]
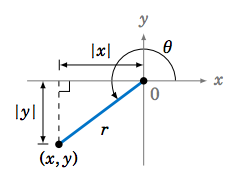
We will now derive one of the most important trigonometric identities. Let \(\theta \) be any angle with a point \((x,y) \) on its terminal side a distance \(r>0 \) from the origin. By the Pythagorean Theorem, \(r^2 = x^2 + y^2 \) (and hence \(r=\sqrt{x^2 + y^2}\)). For example, if \(\theta \) is in QIII as in Figure 3.1.1, then the legs of the right triangle formed by the reference angle have lengths \(|x| \) and \(|y| \) (we use absolute values because \(x \) and \(y \) are negative in QIII). The same argument holds if \(\theta\) is in the other quadrants or on either axis. Thus,
\[ r^2 ~=~ |{x}|^2 ~+~ |{y}|^2 ~=~ x^2 ~+~ y^2 ~,
\nonumber \]
so dividing both sides of the equation by \(r^2 \) (which we can do since \(r>0\)) gives
\[ \frac{r^2}{r^2} ~=~ \frac{x^2 ~+~ y^2}{r^2} ~=~ \frac{x^2}{r^2} ~+~ \frac{y^2}{r^2} ~=~
\left(\frac{x}{r}\right)^2 ~+~ \left(\frac{y}{r}\right)^2 ~.
\nonumber \]
Since \(\frac{r^2}{r^2} = 1 \), \(\frac{x}{r} = \cos\;\theta \), and \(\frac{y}{r} = \sin\;\theta \), we can rewrite this as:
\[\cos^2 \;\theta ~+~ \sin^2 \;\theta ~=~ 1 \label{3.3} \]
You can think of this as sort of a trigonometric variant of the Pythagorean Theorem. Note that we use the notation \(\sin^2 \;\theta \) to mean \((\sin\;\theta)^2 \), likewise for cosine and the other trigonometric functions. We will use the same notation for other powers besides \(2 \).
From the above identity we can derive more identities. For example:
\[ \sin^2 \;\theta ~=~ 1 ~-~ \cos^2 \;\theta \label{3.4} \]
\[ \cos^2 \;\theta ~=~ 1 ~-~ \sin^2 \;\theta \label{3.5} \]
from which we get (after taking square roots):
\[ \sin\;\theta ~=~ \pm\,\sqrt{1 ~-~ \cos^2 \;\theta}\label{3.6} \]
\[\cos\;\theta ~=~ \pm\,\sqrt{1 ~-~ \sin^2 \;\theta}\label{3.7} \]
Also, from the inequalities \(0 \le \sin^2 \;\theta = 1 ~-~ \cos^2 \;\theta \le 1 \) and \(0 \le \cos^2 \;\theta = 1 ~-~ \sin^2 \;\theta \le 1 \), taking square roots gives us the following bounds on sine and cosine:
\[ -1 ~ \le ~ \sin\;\theta ~ \le ~ 1 \label{3.8} \]
\[-1 ~ \le ~ \cos\;\theta ~ \le ~ 1 \label{3.9} \]
The above inequalities are not identities (since they are not equations), but they provide useful checks on calculations. Recall that we derived those inequalities from the definitions of sine and cosine in Section 1.4.
In Equation \ref{3.3}, dividing both sides of the identity by \(\cos^2 \;\theta \) gives
\[ \frac{\cos^2 \;\theta}{\cos^2 \;\theta} ~+~ \frac{\sin^2 \;\theta}{\cos^2 \;\theta} ~=~
\frac{1}{\cos^2 \;\theta} ~~,
\nonumber \]
so since \(\tan\;\theta = \frac{\sin\;\theta}{\cos\;\theta} \) and \(\sec\;\theta = \frac{1}{\cos\;\theta} \), we get:
\[1 ~+~ \tan^2 \;\theta ~=~ \sec^2 \;\theta \label{3.10} \]
Likewise, dividing both sides of Equation \ref{3.3} by \(\sin^2 \;\theta \) gives
\[ \frac{\cos^2 \;\theta}{\sin^2 \;\theta} ~+~ \frac{\sin^2 \;\theta}{\sin^2 \;\theta} ~=~
\frac{1}{\sin^2 \;\theta} ~~,
\nonumber \]
so since \(\cot\;\theta = \frac{\cos\;\theta}{\sin\;\theta} \) and \(\csc\;\theta = \frac{1}{\sin\;\theta} \), we get:
\[\cot^2 \;\theta ~+~ 1 ~=~ \csc^2 \;\theta \label{3.11} \]
Simplify \(\;\cos^2 \;\theta ~ \tan^2 \;\theta\; \).
Solution
We can use Equation \ref{3.5} to simplify:
\[\nonumber \begin{align*}
\cos^2 \;\theta~\tan^2 \;\theta ~ &= ~ \cos^2 \;\theta ~\cdot~
\frac{\sin^2 \;\theta}{\cos^2 \;\theta}\\ \nonumber
&= ~ \sin^2 \;\theta
\end{align*} \nonumber \]
Simplify \(\;5\sin^2 \;\theta ~+~ 4\cos^2 \;\theta\; \).
Solution
We can use Equation \ref{3.1} to simplify:
\[\nonumber \begin{align*}
5\sin^2 \;\theta ~+~ 4\cos^2 \;\theta ~ &= ~ 5\sin^2 \;\theta ~+~
4\left( 1 ~-~ \sin^2 \;\theta \right)\\ \nonumber
&= ~ 5\sin^2 \;\theta ~+~ 4 ~-~ 4\sin^2 \;\theta\\ \nonumber
&= ~ \sin^2 \;\theta ~+~ 4
\end{align*} \nonumber \]
Prove that \(\;\tan \;\theta ~+~ \cot \;\theta ~=~ \sec \;\theta ~ \csc \;\theta\; \).
Solution
We will expand the left side and show that it equals the right side:
\[\nonumber \begin{alignat*}{3}
\tan \;\theta + \cot \;\theta ~ &= ~ \frac{\sin\;\theta}{\cos\;\theta} ~+~
\frac{\cos\;\theta}{\sin\;\theta} &{} \qquad &\text{(by \ref{3.1} and
\ref{3.2})}\\ \nonumber
&= ~ \frac{\sin\;\theta}{\cos\;\theta} \;\cdot\; \frac{\sin\;\theta}{\sin\;\theta} ~+~
\frac{\cos\;\theta}{\sin\;\theta} \;\cdot\; \frac{\cos\;\theta}{\cos\;\theta}
&{} \qquad &\text{(multiply both fractions by \(1\))}\\ \nonumber
&= ~ \frac{\sin^2 \;\theta ~+~ \cos^2 \;\theta}{\cos\;\theta ~ \sin\;\theta} &{} \qquad
&\text{(after getting a common denominator)}\\ \nonumber
&= ~ \frac{1}{\cos\;\theta ~ \sin\;\theta} &{} \qquad &\text{(by \ref{3.3})}\\ \nonumber
&= ~ \frac{1}{\cos\;\theta} ~\cdot~ \frac{1}{\sin\;\theta}\\ \nonumber
&= ~ \sec \;\theta ~ \csc \;\theta
\end{alignat*} \nonumber \]
In the above example, how did we know to expand the left side instead of the right side? In general, though this technique does not always work, the more complicated side of the identity is likely to be easier to expand. The reason is that, by its complexity, there will be more things that you can do with that expression. For example, if you were asked to prove that
\[ \sec\;\theta ~-~ \sin\;\theta ~ \tan\;\theta ~=~ \cos\;\theta ~,
\nonumber \]
there would not be much that you could do with the right side of that identity; it consists of a single term (\(\cos\;\theta\)) that offers no obvious means of expansion.
Prove that \(\;\dfrac{1 ~+~ \cot^2 \;\theta}{\sec\;\theta} ~=~ \csc\;\theta ~ \cot\;\theta\; \).
Solution
Of the two sides, the left side looks more complicated, so we will expand that:
\[\nonumber \begin{alignat*}{3}
\frac{1 ~+~ \cot^2 \;\theta}{\sec\;\theta} ~ &= ~ \frac{\csc^2 \;\theta}{\sec\;\theta}
&{} \qquad &\text{(by \ref{3.11})}\\ \nonumber
&= ~ \dfrac{\csc\;\theta ~\cdot~ \dfrac{1}{\sin\;\theta}}{\dfrac{1}{\cos\;\theta}} &{}
&{}\\[2mm]\nonumber
&= ~ \csc\;\theta ~\cdot~ \frac{\cos\;\theta}{\sin\;\theta} &{} &{}\\ \nonumber
&= ~ \csc \;\theta ~ \cot \;\theta &{} \qquad &\text{(by \ref{3.2})}
\end{alignat*} \nonumber \]
When trying to prove an identity where at least one side is a ratio of expressions, cross-multiplying can be an effective technique:
\[ \frac{a}{b} ~=~ \frac{c}{d} \quad\text{if and only if}\quad ad ~=~ bc
\nonumber \]
Prove that \(\;\dfrac{1 ~+~ \sin\;\theta}{\cos\;\theta} ~=~ \dfrac{\cos\;\theta}{1 ~-~ \sin\;\theta}\; \).
Solution
Cross-multiply and reduce both sides until it is clear that they are equal:
\[\nonumber \begin{align*}
( 1 ~+~ \sin\;\theta ) ( 1 ~-~ \sin\;\theta ) ~ &= ~ \cos\;\theta ~\cdot~ \cos\;\theta\\ \nonumber
1 ~-~ \sin^2 \;\theta ~ &= ~ \cos^2 \;\theta
\end{align*} \nonumber \]
By \ref{3.5} both sides of the last equation are indeed equal. Thus, the original identity holds.
Suppose that \(\;a\,\cos\;\theta = b\; \) and \(\;c\,\sin\;\theta = d\; \) for some angle \(\theta \) and some constants \(a \), \(b \), \(c \), and \(d \). Show that \(\;a^2 c^2 = b^2 c^2 + a^2 d^2 \).
Solution
Multiply both sides of the first equation by \(c \) and the second equation by \(a\):
\[\nonumber \begin{align*}
ac\,\cos\;\theta ~ &= ~ bc\\ \nonumber
ac\,\sin\;\theta ~ &= ~ ad
\end{align*} \nonumber \]
Now square each of the above equations then add them together to get:
\[\nonumber \begin{align*}
(ac\,\cos\;\theta)^2 ~+~ (ac\,\sin\;\theta)^2 ~ &= ~ (bc)^2 ~+~ (ad)^2\\ \nonumber
(ac)^2 \left( \cos^2 \;\theta ~+~ \sin^2 \;\theta \right)~ &= ~ b^2 c^2 ~+~ a^2 d^2\\ \nonumber
a^2 c^2 ~ &= ~ b^2 c^2 ~+~ a^2 d^2 \qquad\text{(by \ref{3.3})}
\end{align*} \nonumber \]
Notice how \(\theta \) does not appear in our final result. The trick was to get a common coefficient (\(ac\)) for \(\;\cos\;\theta\; \) and \(\;\sin\;\theta\; \) so that we could use \(\;\cos^2 \;\theta + \sin^2 \;\theta = 1 \). This is a common technique for eliminating trigonometric functions from systems of equations.


