11.4: Series and Their Notations
- Last updated
- Save as PDF
- Page ID
- 1399
Learning Objectives
- Use summation notation.
- Use the formula for the sum of the first \(n\) terms of an arithmetic series.
- Use the formula for the sum of the first \(n\) terms of a geometric series.
- Use the formula for the sum of an infinite geometric series.
- Solve annuity problems.
A couple decides to start a college fund for their daughter. They plan to invest \($50\) in the fund each month. The fund pays \(6\%\) annual interest, compounded monthly. How much money will they have saved when their daughter is ready to start college in \(6\) years? In this section, we will learn how to answer this question. To do so, we need to consider the amount of money invested and the amount of interest earned.
Using Summation Notation
To find the total amount of money in the college fund and the sum of the amounts deposited, we need to add the amounts deposited each month and the amounts earned monthly. The sum of the terms of a sequence is called a series. Consider, for example, the following series.
\(3+7+11+15+19+ \ldots \nonumber \)
The \(n^{th}\) partial sum of a series is the sum of a finite number of consecutive terms beginning with the first term. The notation \(S_n\) represents the partial sum.
\[\begin{align} S_1 &= 3 \nonumber \\ S_2 &= 3+7=10 \nonumber \\ S_3 &= 3+7+11=21 \nonumber \\ S_4 &= 3+7+11+15 =36 \nonumber \end{align} \nonumber\]
Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma, \(\sum\), to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation, which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation, is the number used to generate the last term in a series.
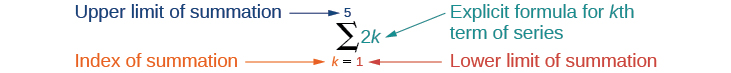
If we interpret the given notation, we see that it asks us to find the sum of the terms in the series \(a_k=2k\) for \(k=1\) through \(k=5\). We can begin by substituting the terms for \(k\) and listing out the terms of this series.
\[\begin{align}a_1 &=2(1)=2 \nonumber \\ a_2 &=2(2)=4 \nonumber \\ a_3 &= 2(3)=6 \nonumber \\ a_4 &= 2(4)=8 \nonumber \\ a_5 &= 2(5)=10 \nonumber \end{align} \nonumber\]
We can find the sum of the series by adding the terms:
\[\sum_{k=1}^{5}2k=2+4+6+8+10=30 \nonumber\]
Definition: SUMMATION NOTATION
The sum of the first \(n\) terms of a series can be expressed in summation notation as follows:
\[\sum_{k=1}^{n}a_k\]
This notation tells us to find the sum of \(a_k\) from \(k=1\) to \(k=n\).
\(k\) is called the index of summation, \(1\) is the lower limit of summation, and \(n\) is the upper limit of summation.
Q&A: Does the lower limit of summation have to be 1?
No. The lower limit of summation can be any number, but \(1\) is frequently used. We will look at examples with lower limits of summation other than \(1\).
How to: Given summation notation for a series, evaluate the value
- Identify the lower limit of summation.
- Identify the upper limit of summation.
- Substitute each value of \(k\) from the lower limit to the upper limit into the formula.
- Add to find the sum.
Example \(\PageIndex{1}\): Using Summation Notation
Evaluate
\(\sum_{k=3}^{7}k^2\)
Solution
According to the notation, the lower limit of summation is \(3\) and the upper limit is \(7\). So we need to find the sum of \(k^2\) from \(k=3\) to \(k=7\). We find the terms of the series by substituting \(k=3, 4, 5, 6,\) and \(7\) into the function \(k^2\). We add the terms to find the sum.
\[\begin{align}\sum_{k=3}^{7}k^2 &= 3^2+4^2+5^2+6^2+7^2 \nonumber \\[4pt] &= 9+16+25+36+49 \nonumber \\[4pt] &= 135 \nonumber \end{align} \nonumber\]
Exercise \(\PageIndex{1}\)
Evaluate
\(\sum_{k=2}^{5}(3k–1)\)
- Answer
-
\(38\)
Using the Formula for Arithmetic Series
Just as we studied special types of sequences, we will look at special types of series. Recall that an arithmetic sequence is a sequence in which the difference between any two consecutive terms is the common difference, \(d\). The sum of the terms of an arithmetic sequence is called an arithmetic series. We can write the sum of the first \(n\) terms of an arithmetic series as:
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n. \nonumber \]
We can also reverse the order of the terms and write the sum as
\[S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1. \nonumber\]
If we add these two expressions for the sum of the first \(n\) terms of an arithmetic series, we can derive a formula for the sum of the first \(n\) terms of any arithmetic series.
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n \nonumber\]
\[\underline{+S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1} \nonumber\]
\[2S_n=(a_1+a_n)+(a_1+a_n)+...+(a_1+a_n) \nonumber\]
Because there are \(n\) terms in the series, we can simplify this sum to
\[2S_n=n(a_1+a_n). \nonumber \]
We divide by \(2\) to find the formula for the sum of the first \(n\) terms of an arithmetic series.
\[S_n=\dfrac{n(a_1+a_n)}{2} \nonumber \]
FORMULA FOR THE SUM OF THE FIRST \(N\) TERMS OF AN ARITHMETIC SERIES
An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of the first \(n\) terms of an arithmetic sequence is
\[S_n=\dfrac{n(a_1+a_n)}{2}\]
How to: Given terms of an arithmetic series, find the sum of the first \(n\) terms
- Identify \(a_1\) and \(a_n\).
- Determine \(n\).
- Substitute values for \(a_1\), \(a_n\), and \(n\) into the formula \(S_n=\dfrac{n(a_1+a_n)}{2}\).
- Simplify to find \(S_n\).
Terms of an Arithmetic Series
Find the sum of each arithmetic series.
- \(5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 + 32\)
- \(20 + 15 + 10 +…+ −50\)
- \(\sum_{k=1}^{12}3k−8\)
Solution
- We are given \(a_1=5\) and \(a_n=32\).
Count the number of terms in the sequence to find \(n=10\).
Substitute values for \(a_1\), \(a_n\), and \(n\) into the formula and simplify.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{10}&=\dfrac{10(5+32)}{2}\\ &=185 \end{align*}\]
- We are given \(a_1=20\) and \(a_n=−50\).
Use the formula for the general term of an arithmetic sequence to find \(n\).
\[\begin{align*} a_n&=a_1+(n-1)d\\ -50&=20+(n-1)(-5)\\ -70&=(n-1)(-5)\\ 14&=n-1\\ 15&=n \end{align*}\]
Substitute values for \(a_1\), \(a_n\), \(n\) into the formula and simplify.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{15}&=\dfrac{15(20-50)}{2}\\ &=-225 \end{align*}\]
- To find \(a_1\), substitute \(k=1\) into the given explicit formula.
\[\begin{align*} a_k&=3k-8\\ a_1&=3(1)-8\\ &=-5 \end{align*}\]
We are given that \(n=12\). To find \(a_12\), substitute \(k=12\) into the given explicit formula.
\[\begin{align*} a_k&=3k-8\\ a_{12}&=3(12)-8\\ &=28 \end{align*}\]
Substitute values for \(a_1\), \(a_n\), and \(n\) into the formula and simplify.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{12}&=\dfrac{12(-5+28)}{2}\\ &=138 \end{align*}\]
Use the formula to find the sum of each arithmetic series.
Exercise \(\PageIndex{2A}\)
\(1.4 + 1.6 + 1.8 + 2.0 + 2.2 + 2.4 + 2.6 + 2.8 + 3.0 + 3.2 + 3.4\)
- Answer
-
\(26.4\)
Exercise \(\PageIndex{2B}\)
\(13 + 21 + 29 + …+ 69\)
- Answer
-
\(328\)
Exercise \(\PageIndex{2C}\)
\(\sum_{k=1}{10}5−6k\)
- Answer
-
\(−280\)
Example \(\PageIndex{3}\): Solving Application Problems with Arithmetic Series
On the Sunday after a minor surgery, a woman is able to walk a half-mile. Each Sunday, she walks an additional quarter-mile. After \(8\) weeks, what will be the total number of miles she has walked?
Solution
This problem can be modeled by an arithmetic series with \(a_1=\dfrac{1}{2}\) and \(d=\dfrac{1}{4}\). We are looking for the total number of miles walked after \(8\) weeks, so we know that \(n=8\), and we are looking for \(S_8\). To find \(a_8\), we can use the explicit formula for an arithmetic sequence.
\[\begin{align*} a_n&=a_1+d(n-1)\\ a_8&=\dfrac{1}{2}+\dfrac{1}{4}(8-1)\\ &=\dfrac{9}{4} \end{align*}\]
We can now use the formula for arithmetic series.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_8&=\dfrac{8\left(\dfrac{1}{2}+\dfrac{9}{4}\right)}{2}\\ &=11 \end{align*}\]
She will have walked a total of \(11\) miles.
Exercise \(\PageIndex{3}\)
A man earns \($100\) in the first week of June. Each week, he earns \($12.50\) more than the previous week. After \(12\) weeks, how much has he earned?
- Answer
-
\($2,025\)
Using the Formula for Geometric Series
Just as the sum of the terms of an arithmetic sequence is called an arithmetic series, the sum of the terms in a geometric sequence is called a geometric series. Recall that a geometric sequence is a sequence in which the ratio of any two consecutive terms is the common ratio, \(r\). We can write the sum of the first \(n\) terms of a geometric series as
\(S_n=a_1+ra_1+r^2a_1+...+r^{n–1}a_1\).
Just as with arithmetic series, we can do some algebraic manipulation to derive a formula for the sum of the first \(n\) terms of a geometric series. We will begin by multiplying both sides of the equation by \(r\).
\(rS_n=ra_1+r^2a_1+r^3a_1+...+r^na_1\)
Next, we subtract this equation from the original equation.
\[\begin{align*} S_n&=a_1+ra_1+r^2a_1+...+r^{n-1}a_1\\ \underline{-rS_n}&=\underline{-(ra_1+r^2a_1+r^3a_1+...+r^na_1)}\\ (1-r)S_n&=a_1-r^na_1 \end{align*}\]
Notice that when we subtract, all but the first term of the top equation and the last term of the bottom equation cancel out. To obtain a formula for \(S_n\), divide both sides by \((1−r)\).
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\) \(r≠1\)
TERMS OF A GEOMETRIC SERIES
A geometric series is the sum of the terms in a geometric sequence. The formula for the sum of the first \(n\) terms of a geometric sequence is represented as
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\) \(r≠1\)
How to: Given a geometric series, find the sum of the first \(n\) terms.
- Identify \(a_1\), \(r\), and \(n\).
- Substitute values for \(a_1\), \(r\), and \(n\) into the formula \(S_n=\dfrac{a_1(1−r^n)}{1−r}\).
- Simplify to find \(S_n\).
Terms of a Geometric Series
Use the formula to find the indicated partial sum of each geometric series.
- \(S_{11}\) for the series \(8 + -4 + 2 + …\)
- \(\sum_{ 6}^{k=1}3⋅2k\)
Solution
- \(a_1=8\), and we are given that \(n=11\).
We can find \(r\) by dividing the second term of the series by the first.
\(r=\dfrac{−4}{8}=−\dfrac{1}{2}\)
Substitute values for \(a_1\), \(r\), and \(n\) into the formula and simplify.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_{11}&=\dfrac{8\left(1-{\left(-\dfrac{1}{2}\right)}^{11}\right)}{1-\left(-\dfrac{1}{2}\right)}\\ &\approx 5.336 \end{align*}\]
- Find \(a_1\) by substituting \(k=1\) into the given explicit formula.
\(a_1=3⋅2^1=6\)
We can see from the given explicit formula that \(r=2\). The upper limit of summation is \(6\), so \(n=6\).
Substitute values for \(a_1\), \(r\), and \(n\) into the formula, and simplify.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_6&=\dfrac{6(1-2^6)}{1-2}\\ &=378 \end{align*}\]
Use the formula to find the indicated partial sum of each geometric series.
Exercise \(\PageIndex{4A}\)
\(S_{20}\) for the series \(1,000 + 500 + 250 + …\)
- Answer
-
\(≈2,000.00\)
Exercise \(\PageIndex{4B}\)
\(\sum_{k=1}^{8}3^k\)
- Answer
-
\(9,840\)
Example \(\PageIndex{5}\): Solving an Application Problem with a Geometric Series
At a new job, an employee’s starting salary is \($26,750\). He receives a \(1.6\%\) annual raise. Find his total earnings at the end of \(5\) years.
Solution
The problem can be represented by a geometric series with \(a_1=26,750\); \(n=5\); and \(r=1.016\). Substitute values for \(a_1\), \(r\), and \(n\) into the formula and simplify to find the total amount earned at the end of \(5\) years.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_5&=\dfrac{26,750(1-{1.016}^5)}{1-1.016}\\ &\approx 138,099.03 \end{align*}\]
He will have earned a total of \($138,099.03\) by the end of \(5\) years.
Exercise \(\PageIndex{5}\)
At a new job, an employee’s starting salary is \($32,100\). She receives a \(2\%\) annual raise. How much will she have earned by the end of \(8\) years?
- Answer
-
\($275,513.31\)
Using the Formula for the Sum of an Infinite Geometric Series
Thus far, we have looked only at finite series. Sometimes, however, we are interested in the sum of the terms of an infinite sequence rather than the sum of only the first \(n\) terms. An infinite series is the sum of the terms of an infinite sequence. An example of an infinite series is \(2+4+6+8+...\)
This series can also be written in summation notation as \(\sum_{k=1}^{\infty}2k\), where the upper limit of summation is infinity. Because the terms are not tending to zero, the sum of the series increases without bound as we add more terms. Therefore, the sum of this infinite series is not defined. When the sum is not a real number, we say the series diverges.
Determining Whether the Sum of an Infinite Geometric Series is Defined
If the terms of an infinite geometric series approach \(0\), the sum of an infinite geometric series can be defined. The terms in this series approach \(0\):
\(1+0.2+0.04+0.008+0.0016+...\)
The common ratio \(r = 0.2\). As \(n\) gets very large, the values of \(r^n\) get very small and approach \(0\). Each successive term affects the sum less than the preceding term. As each succeeding term gets closer to \(0\), the sum of the terms approaches a finite value. The terms of any infinite geometric series with \(−1<r<1\) approach \(0\); the sum of a geometric series is defined when \(−1<r<1\).
DETERMINING WHETHER THE SUM OF AN INFINITE GEOMETRIC SERIES IS DEFINED
The sum of an infinite series is defined if the series is geometric and \(−1<r<1\).
How to: Given the first several terms of an infinite series, determine if the sum of the series exists.
- Find the ratio of the second term to the first term.
- Find the ratio of the third term to the second term.
- Continue this process to ensure the ratio of a term to the preceding term is constant throughout. If so, the series is geometric.
- If a common ratio, \(r\), was found in step 3, check to see if \(−1<r<1\). If so, the sum is defined. If not, the sum is not defined.
Example \(\PageIndex{6}\): Determining Whether the Sum of an Infinite Series is Defined
Determine whether the sum of each infinite series is defined.
- \(12 + 8 + 4 + …\)
- \(\dfrac{3}{4}+\dfrac{1}{2}+\dfrac{1}{3}+...\)
- \(\sum_{k=1}^{\infty}27⋅{(\dfrac{1}{3})}^k\)
- \(\sum_{k=1}^{\infty}5k\)
Solution
- The ratio of the second term to the first is \(\dfrac{2}{3}\), which is not the same as the ratio of the third term to the second, \(\dfrac{1}{2}\).The series is not geometric.
- The ratio of the second term to the first is the same as the ratio of the third term to the second. The series is geometric with a common ratio of \(\dfrac{2}{3}\). The sum of the infinite series is defined.
- The given formula is exponential with a base of \(\dfrac{1}{3}\); the series is geometric with a common ratio of \(\dfrac{1}{3}\). The sum of the infinite series is defined.
- The given formula is not exponential; the series is not geometric because the terms are increasing, and so cannot yield a finite sum.
Determine whether the sum of the infinite series is defined.
Exercise \(\PageIndex{6A}\)
\(\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{9}{8}+...\)
- Answer
-
The sum is defined. It is geometric.
Exercise \(\PageIndex{6B}\)
\(24+(−12)+6+(−3)+...\)
- Answer
-
The sum of the infinite series is defined.
Exercise \(\PageIndex{6C}\)
\(\sum_{k=1}^{\infty}15⋅{(–0.3)}^k\)
- Answer
-
The sum of the infinite series is defined.
Finding Sums of Infinite Series
When the sum of an infinite geometric series exists, we can calculate the sum. The formula for the sum of an infinite series is related to the formula for the sum of the first \(n\) terms of a geometric series.
\[S_n=\dfrac{a_1(1−r^n)}{1−r}\]
We will examine an infinite series with \(r=\dfrac{1}{2}\). What happens to \(r^n\) as \(n\) increases?
\[\begin{align*} \left(\dfrac{1}{2}\right)^2&=\dfrac{1}{4}\\ \left(\dfrac{1}{2}\right)^3&=\dfrac{1}{8}\\ \left(\dfrac{1}{2}\right)^4&=\dfrac{1}{16} \end{align*}\]
The value of \(r^n\) decreases rapidly. What happens for greater values of \(n\)?
\[\begin{align*} {\left(\dfrac{1}{2}\right)}^{10} &= \dfrac{1}{1,024} \\ {\left(\dfrac{1}{2}\right)}^{20} &= \dfrac{1}{1,048,576} \\ {\left(\dfrac{1}{2}\right)}^{30} &= \dfrac{1}{1,073,741,824} \end{align*}\]
As \(n\) gets very large, \(r^n\) gets very small. We say that, as \(n\) increases without bound, \(r^n\) approaches 0. As \(r^n\) approaches \(0\), \(1\), \(−r^n\) approaches \(1\). When this happens, the numerator approaches \(a_1\). This give us a formula for the sum of an infinite geometric series.
FORMULA FOR THE SUM OF AN INFINITE GEOMETRIC SERIES
The formula for the sum of an infinite geometric series with \(−1<r<1\) is
\[S=\dfrac{a_1}{1−r}\]
How to: Given an infinite geometric series, find its sum
- Identify \(a_1\) and \(r\).
- Confirm that \(–1<r<1\).
- Substitute values for \(a_1\) and \(r\) into the formula, \(S=\dfrac{a_1}{1−r}\).
- Simplify to find \(S\).
Example \(\PageIndex{7A}\): Finding the Sum of an Infinite Geometric Series
Find the sum, if it exists, for the following:
- \(10+9+8+7+…\)
- \(248.6+99.44+39.776 + …\)
- \(\sum_{k=1}^{\infty}4,374⋅{(–\dfrac{1}{3})}^{k–1}\)
- \(\sum_{k=1}^{\infty}\dfrac{1}{9}⋅{(\dfrac{4}{3})}^k\)
Solution
- There is not a constant ratio; the series is not geometric.
- There is a constant ratio; the series is geometric. \(a_1=248.6\) and \(r=\dfrac{99.44}{248.6}=0.4\), so the sum exists. Substitute \(a_1=248.6\) and \(r=0.4\) into the formula and simplify to find the sum:
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &=\dfrac{248.6}{1−0.4} \\[4pt] &=414.\overline{3} \end{align*}\]
- The formula is exponential, so the series is geometric with \(r=–\dfrac{1}{3}\). Find \(a_1\) by substituting \(k=1\) into the given explicit formula:
\(a_1=4,374⋅{(–\dfrac{1}{3})}^{1–1}=4,374\)
Substitute \(a_1=4,374\) and \(r=−\dfrac{1}{3}\) into the formula, and simplify to find the sum:
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &= \dfrac{4,374}{1−\left(−\dfrac{1}{3}\right)} \\[4pt] &= 3,280.5 \end{align*}\]
- The formula is exponential, so the series is geometric, but \(r>1\). The sum does not exist.
Example \(\PageIndex{7B}\): Finding an Equivalent Fraction for a Repeating Decimal
Find an equivalent fraction for the repeating decimal \(0.\overline{3}\)
Solution
We notice the repeating decimal \(0.\overline{3}=0.333...\) so we can rewrite the repeating decimal as a sum of terms.
\(0.\overline{3}=0.3+0.03+0.003+...\)
Looking for a pattern, we rewrite the sum, noticing that we see the first term multiplied to \(0.1\) in the second term, and the second term multiplied to \(0.1\) in the third term.

Notice the pattern; we multiply each consecutive term by a common ratio of \(0.1\) starting with the first term of \(0.3\). So, substituting into our formula for an infinite geometric sum, we have
\(S_n=\dfrac{a_1}{1−r}=\dfrac{0.3}{1−0.1}=\dfrac{0.3}{0.9}=\dfrac{1}{3}\).
Find the sum, if it exists.
Exercise \(\PageIndex{7A}\)
\(2+23+29+...\)
- Answer
-
\(3\)
Exercise \(\PageIndex{7B}\)
\(\sum_{k=1}^{\infty}0.76k+1\)
- Answer
-
The series is not geometric.
Exercise \(\PageIndex{7C}\)
\(\sum_{k=1}^{\infty}{\left(−\dfrac{3}{8}\right)}^k\)
- Answer
-
\(−\dfrac{3}{11}\)
Solving Annuity Problems
At the beginning of the section, we looked at a problem in which a couple invested a set amount of money each month into a college fund for six years. An annuity is an investment in which the purchaser makes a sequence of periodic, equal payments. To find the amount of an annuity, we need to find the sum of all the payments and the interest earned. In the example, the couple invests \($50\) each month. This is the value of the initial deposit. The account paid \(6\%\) annual interest, compounded monthly. To find the interest rate per payment period, we need to divide the \(6\%\) annual percentage interest (APR) rate by \(12\). So the monthly interest rate is \(0.5\%\). We can multiply the amount in the account each month by \(100.5\%\) to find the value of the account after interest has been added.
We can find the value of the annuity right after the last deposit by using a geometric series with \(a_1=50\) and \(r=100.5%=1.005\). After the first deposit, the value of the annuity will be \($50\). Let us see if we can determine the amount in the college fund and the interest earned.
We can find the value of the annuity after nn deposits using the formula for the sum of the first nn terms of a geometric series. In \(6\) years, there are \(72\) months, so \(n=72\). We can substitute \(a_1=50\), \(r=1.005\), and \(n=72\) into the formula, and simplify to find the value of the annuity after 6 years.
\(S_{72}=\dfrac{50(1−{1.005}^{72})}{1−1.005}≈4,320.44\)
After the last deposit, the couple will have a total of \($4,320.44\) in the account. Notice, the couple made \(72\) payments of \($50\) each for a total of \(72(50) = $3,600\). This means that because of the annuity, the couple earned \($720.44\) interest in their college fund.
How to: Given an initial deposit and an interest rate, find the value of an annuity.
- Determine \(a_1\), the value of the initial deposit.
- Determine \(n\), the number of deposits.
- Determine \(r\).
- Divide the annual interest rate by the number of times per year that interest is compounded.
- Add 1 to this amount to find \(r\).
- Substitute values for \(a_1\), \(r\), and \(n\) into the formula for the sum of the first nn terms of a geometric series, \(S_n=\dfrac{a_1(1–r^n)}{1–r}\).
- Simplify to find \(S_n\), the value of the annuity after \(n\) deposits.
Example \(\PageIndex{8}\): Solving an Annuity Problem
A deposit of \($100\) is placed into a college fund at the beginning of every month for \(10\) years. The fund earns \(9\%\) annual interest, compounded monthly, and paid at the end of the month. How much is in the account right after the last deposit?
Solution
The value of the initial deposit is \($100\), so \(a_1=100\). A total of \(120\) monthly deposits are made in the \(10\) years, so \(n=120\). To find \(r\), divide the annual interest rate by \(12\) to find the monthly interest rate and add \(1\) to represent the new monthly deposit.
\(r=1+\dfrac{0.09}{12}=1.0075\)
Substitute \(a_1=100\), \(r=1.0075\), and \(n=120\) into the formula for the sum of the first \(n\) terms of a geometric series, and simplify to find the value of the annuity.
\(S_{120}=\dfrac{100(1−{1.0075}^{120})}{1−1.0075}≈19,351.43\)
So the account has $19,351.43 after the last deposit is made.
Exercise \(\PageIndex{8}\)
At the beginning of each month, \($200\) is deposited into a retirement fund. The fund earns \(6\%\) annual interest, compounded monthly, and paid into the account at the end of the month. How much is in the account if deposits are made for \(10\) years?
- Answer
-
\($92,408.18\)
Media
Access these online resources for additional instruction and practice with series.
Key Equations
| sum of the first \(n\) terms of an arithmetic series | \(S_n=\dfrac{n(a_1+a_n)}{2}\) |
| sum of the first \(n\) terms of a geometric series | \(S_n=\dfrac{a_1(1−r^n)}{1−r}\)⋅ \(r≠1\) |
| sum of an infinite geometric series with \(–1<r< 1\) | \(S_n=\dfrac{a_1}{1−r}\)⋅ \(r≠1\) |
Key Concepts
- The sum of the terms in a sequence is called a series.
- A common notation for series is called summation notation, which uses the Greek letter sigma to represent the sum. See Example \(\PageIndex{1}\).
- The sum of the terms in an arithmetic sequence is called an arithmetic series.
- The sum of the first \(n\) terms of an arithmetic series can be found using a formula. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
- The sum of the terms in a geometric sequence is called a geometric series.
- The sum of the first \(n\) terms of a geometric series can be found using a formula. See Example \(\PageIndex{4}\) and Example \(\PageIndex{5}\).
- The sum of an infinite series exists if the series is geometric with \(–1<r<1\).
- If the sum of an infinite series exists, it can be found using a formula. See Example \(\PageIndex{6}\), Example \(\PageIndex{7}\), and Example \(\PageIndex{8}\).
- An annuity is an account into which the investor makes a series of regularly scheduled payments. The value of an annuity can be found using geometric series. See Example \(\PageIndex{9}\).


