4.3: Area of a Sector
- Page ID
- 3326
In geometry you learned that the area of a circle of radius \(r \) is \(\pi r^2 \). We will now learn how to find the area of a sector of a circle. A sector is the region bounded by a central angle and its intercepted arc, such as the shaded region in Figure 4.3.1.
Let \(\theta \) be a central angle in a circle of radius \(r \) and let \(A \) be the area of its sector. Similar to arc length, the ratio of \(A \) to the area of the entire circle is the same as the ratio of \(\theta \) to one revolution. In other words, again using radian measure,
\[ \frac{\text{area of sector}}{\text{area of entire circle}} ~=~
\frac{\text{sector angle}}{\text{one revolution}} \quad\Rightarrow\quad
\frac{A}{\pi\,r^2} ~=~ \frac{\theta}{2\pi} ~.
\nonumber \]
Solving for \(A \) in the above equation, we get the following formula:
In a circle of radius \(r \), the area \(A \) of the sector inside a central angle \(\theta \) is
\[ A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~,\label{eqn:sectorarea} \]
where \(\theta \) is measured in radians.
Find the area of a sector whose angle is \(\frac{\pi}{5} \) rad in a circle of radius \(4\) cm.
Solution
Using \(\theta=\frac{\pi}{5} \) and \(r=4 \) in Equation \ref{eqn:sectorarea}, the area \(A \) of the sector is
\[ A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~= \tfrac{1}{2}\,(4)^2 \;\cdot\;\tfrac{\pi}{5}
~=~ \boxed{\tfrac{8\pi}{5}~\text{cm}^2} ~.
\nonumber \]
Find the area of a sector whose angle is \(117^\circ \) in a circle of radius \(3.5 \) m.
Solution:
As with arc length, we have to make sure that the angle is measured in radians or else the answer will be way off. So converting \(\theta=117^\circ \) to radians and using \(r=3.5 \) in Equation \ref{eqn:sectorarea} for the area \(A \) of the sector, we get
\[ \theta ~=~ 117^\circ ~=~ \frac{\pi}{180} \;\cdot\; 117 ~=~ 2.042~\text{rad}
\quad\Rightarrow\quad
A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~= \tfrac{1}{2}\,(3.5)^2 \;(2.042)
~=~ \boxed{12.51~\text{m}^2} ~.
\nonumber \]
For a sector whose angle is \(\theta \) in a circle of radius \(r \), the length of the arc cut off by that angle is \(s=r\,\theta \). Thus, by Equation \ref{eqn:sectorarea} the area \(A \) of the sector can be written as:
\[
\boxed{ A ~=~ \tfrac{1}{2}\,rs}\label{eqn:sectorarc}
\nonumber \]
Note: The central angle \(\theta \) that intercepts an arc is sometimes called the angle subtended by the arc.
Find the area of a sector whose arc is \(6 \) cm in a circle of radius \(9 \) cm.
Solution
Using \(s=6 \) and \(r=9 \) in Equation \ref{eqn:sectorarc} for the area \(A \), we get
\[ A ~=~ \tfrac{1}{2}\,rs ~=~ ~=~ \tfrac{1}{2}\,(9)\,(6) ~=~ \boxed{27~\text{cm}^2} ~.
\nonumber \]
Note that the angle subtended by the arc is \(\theta = \frac{s}{r} = \frac{2}{3} \) rad.
Find the area \(K \) inside the belt pulley system from Example 4.7 in Section 4.2.
Solution:
Recall that the belt pulleys have radii of \(5 \) cm and \(8 \) cm, and their centers are \(15 \) cm apart. We showed in Example 4.7 that \(EF=AC=6\,\sqrt{6} \), \(\angle\,DAE=1.37 \) rad, and \(\angle\,GBF=1.77 \) rad. We see from Figure 4.3.2 that, by symmetry, the total area \(K \) enclosed by the belt is twice the area above the line \(\overline{DG} \), that is,
\[\nonumber \begin{align*}
K ~=~ 2\,( (&\text{Area of sector \(DAE\)}) ~+~ (\text{Area of rectangle \(AEFC\)})\\ \nonumber
&+~ (\text{Area of triangle \(\triangle\,ABC\)}) ~+~ (\text{Area of sector \(GBF\)}) )~.
\end{align*} \nonumber \]
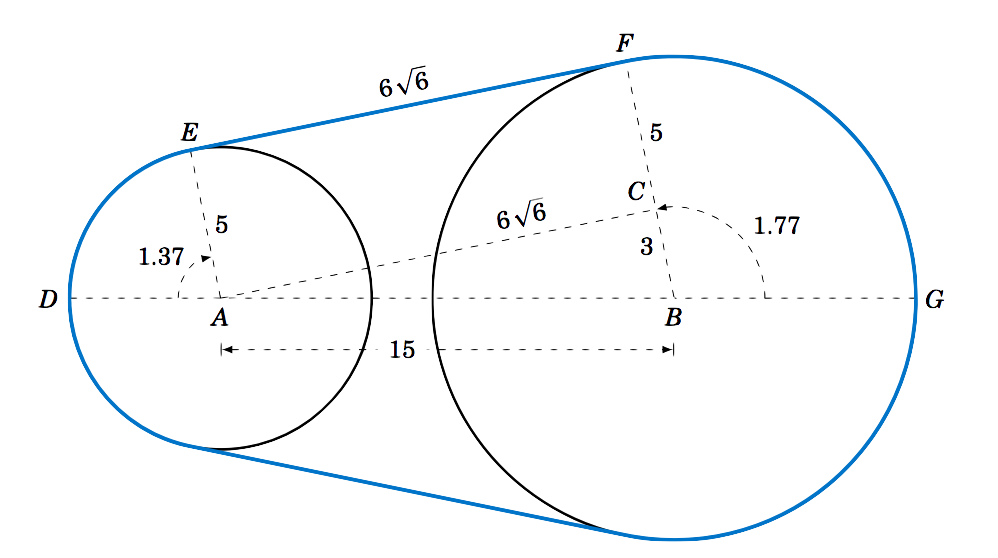
Since \(AEFC \) is a rectangle with sides \(5 \) and \(6\,\sqrt{6} \), its area is \(30\,\sqrt{6} \). And since \(\triangle\,ABC \) is a right triangle whose legs have lengths \(3 \) and \(6\,\sqrt{6} \), its area is \(\frac{1}{2}\,(3)\,(6\,\sqrt{6}) = 9\,\sqrt{6} \). Thus, using Equation \ref{eqn:sectorarea} for the areas of sectors \(DAE \) and \(GBF \), we have
\[\nonumber \begin{align*}
K ~&=~ 2\,\left( (\text{Area of sector \(DAE\)}) \;+\; 30\,\sqrt{6} \;+\; 9\,\sqrt{6} \;+\;
(\text{Area of sector \(GBF\)}) \right)\\ \nonumber
&=~ 2\,\left( \tfrac{1}{2}\,(5)^2 \,(1.37) ~+~ 30\,\sqrt{6} ~+~ 9\,\sqrt{6} ~+~
\tfrac{1}{2}\,(8)^2 \,(1.77) \right)\\ \nonumber
&=~ \boxed{338.59~\text{cm}^2}~.
\end{align*}
\nonumber \]
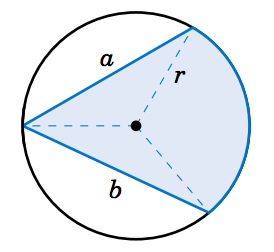
So far we have dealt with the area cut off by a central angle. How would you find the area of a region cut off by an inscribed angle, such as the shaded region in Figure 4.3.3? In this picture, the center of the circle is inside the inscribed angle, and the lengths \(a \) and \(b\) of the two chords are given, as is the radius \(r \) of the circle. Drawing line segments from the center of the circle to the endpoints of the chords indicates how to solve this problem: add up the areas of the two triangles and the sector formed by the central angle. The areas and angles of the two triangles can be determined (since all three sides are known) using methods from Chapter 2. Also, recall (Theorem 2.4 in Section 2.5) that a central angle has twice the measure of any inscribed angle which intercepts the same arc. In the exercises you will be asked to solve problems like this (including the cases where the center of the circle is outside or on the inscribed angle).
Another type of region we can consider is a segment of a circle, which is the region between a chord and the arc it cuts off. In Figure 4.3.4 the segment formed by the chord \(\overline{AB} \) is the shaded region between the arc \(\overparen{AB} \) and the triangle \(\triangle\,OAB \). By Equation 2.23 in Section 2.4 for the area of a triangle given two sides and their included angle, we know that
\[ \text{area of } \triangle\,OAB ~=~ \tfrac{1}{2}\,(r)\,(r)\,\sin\;\theta ~=~
\tfrac{1}{2}\,r^2 \,\sin\;\theta ~.
\nonumber \]
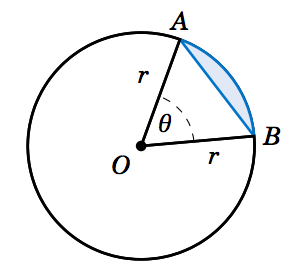
Thus, since the area \(K \) of the segment is the area of the sector \(AOB \) minus the area of the triangle \(\triangle\,OAB \), we have
\[
\text{area \(K \) of segment } AB ~=~ \tfrac{1}{2}\,r^2 \;\theta ~-~ \tfrac{1}{2}\,r^2 \,\sin\;\theta
~=~ \boxed{\tfrac{1}{2}\,r^2 \,(\theta - \sin\;\theta)} ~.\label{eqn:segment}
\nonumber \]
Note that as a consequence of Equation \ref{eqn:segment} we must have \(\;\theta > \sin\;\theta\) for \(0 < \theta \le \pi \) (measured in radians), since the area of a segment is positive for those angles.
Find the area of the segment formed by a chord of length \(3 \) in a circle of radius \(2 \).
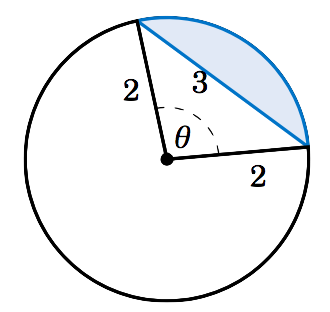
Figure 4.3.5
Solution
Figure 4.3.5 shows the segment formed by a chord of length \(3 \) in a circle of radius \(r=2 \). We can use the Law of Cosines to find the subtended central angle \(\theta\):
\[ \cos\;\theta ~=~ \frac{2^2 + 2^2 - 3^2}{2\,(2)\,(2)} ~=~ -0.125 \quad\Rightarrow\quad
\theta ~=~ 1.696~\text{rad}
\nonumber \]
Thus, by Equation \ref{eqn:segment} the area \(K \) of the segment is:
\[ K ~=~ \tfrac{1}{2}\,r^2 \,(\theta - \sin\;\theta) ~=~ \tfrac{1}{2}\,(2)^2 \,
(1.696 - \sin\;1.696) ~=~ \boxed{1.408}
\nonumber \]
The centers of two circles are \(7 \) cm apart, with one circle having a radius of \(5 \) cm and the other a radius of \(4 \) cm. Find the area \(K \) of their intersection.
Solution:
In Figure 4.3.6(a), we see that the intersection of the two circles is the union of the segments formed by the chord \(\overline{CD} \) in each circle. Thus, once we determine the angles \(\angle\,CAD \) and \(\angle\,CBD \) we can calculate the area of each segment and add those areas together to get \(K \).
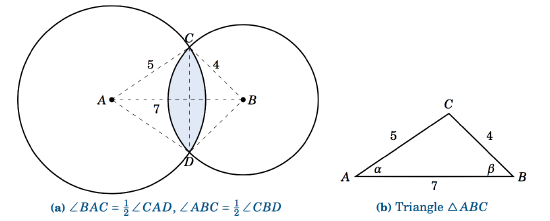
By symmetry, we see that \(\angle\,BAC = \frac{1}{2}\,\angle\,CAD \) and \(\angle\,ABC = \frac{1}{2}\,\angle\,CBD \). So let \(\alpha = \angle\,BAC \) and \(\beta = \angle\,ABC \), as in Figure 4.3.6(b). By the Law of Cosines, we have
\[ \begin{alignat*}{7}
\cos\;\alpha ~&=~ \frac{7^2 + 5^2 - 4^2}{2\,(7)\,(5)} ~&=~ 0.8286 \quad&\Rightarrow\quad
\alpha ~&=~ 0.594~\text{rad} \quad&\Rightarrow\quad \angle\,CAD ~&=~2\,(0.594) = 1.188~\text{rad}\\ \nonumber
\cos\;\beta ~&=~ \frac{7^2 + 4^2 - 5^2}{2\,(7)\,(4)} ~&=~ 0.7143 \quad&\Rightarrow\quad
\beta ~&=~ 0.775~\text{rad} \quad&\Rightarrow\quad \angle\,CBD ~&=~ 2\,(0.775) = 1.550~\text{rad}
\end{alignat*} \nonumber \]
Thus, the area \(K \) is
\[\nonumber \begin{align*}
K ~&=~ (\text{Area of segment \(CD \) in circle at \(A\)}) ~+~
(\text{Area of segment \(CD \) in circle at \(B\)})\\ \nonumber
&=~ \tfrac{1}{2}\,(5)^2 \,(1.188 - \sin\;1.188) ~+~ \tfrac{1}{2}\,(4)^2 \,(1.550 - \sin\;1.550)\\ \nonumber
&=~ \boxed{7.656~\text{cm}^2} ~.
\end{align*} \nonumber \]


