9.2: Systems of Linear Equations - Three Variables
- Last updated
- Save as PDF
- Page ID
- 1384
Learning Objectives
- Solve systems of three equations in three variables.
- Identify inconsistent systems of equations containing three variables.
- Express the solution of a system of dependent equations containing three variables.
John received an inheritance of \($12,000\) that he divided into three parts and invested in three ways: in a money-market fund paying \(3\%\) annual interest; in municipal bonds paying \(4\%\) annual interest; and in mutual funds paying \(7\%\) annual interest. John invested \($4,000\) more in municipal funds than in municipal bonds. He earned \($670\) in interest the first year. How much did John invest in each type of fund?

Figure \(\PageIndex{1}\): (credit: “Elembis,” Wikimedia Commons)
Understanding the correct approach to setting up problems such as this one makes finding a solution a matter of following a pattern. We will solve this and similar problems involving three equations and three variables in this section. Doing so uses similar techniques as those used to solve systems of two equations in two variables. However, finding solutions to systems of three equations requires a bit more organization and a touch of visual gymnastics.
Solving Systems of Three Equations in Three Variables
In order to solve systems of equations in three variables, known as three-by-three systems, the primary tool we will be using is called Gaussian elimination, named after the prolific German mathematician Karl Friedrich Gauss. While there is no definitive order in which operations are to be performed, there are specific guidelines as to what type of moves can be made. We may number the equations to keep track of the steps we apply. The goal is to eliminate one variable at a time to achieve upper triangular form, the ideal form for a three-by-three system because it allows for straightforward back-substitution to find a solution \((x,y,z)\), which we call an ordered triple. A system in upper triangular form looks like the following:
\[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]
The third equation can be solved for \(z\),and then we back-substitute to find \(y\) and \(x\). To write the system in upper triangular form, we can perform the following operations:
- Interchange the order of any two equations.
- Multiply both sides of an equation by a nonzero constant.
- Add a nonzero multiple of one equation to another equation.
The solution set to a three-by-three system is an ordered triple \({(x,y,z)}\). Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.
NUMBER OF POSSIBLE SolutionS
Figure \(\PageIndex{2}\) and Figure \(\PageIndex{3}\) illustrate possible solution scenarios for three-by-three systems.
- Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple \({(x,y,z)}\). Graphically, the ordered triple defines a point that is the intersection of three planes in space.
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as \(0=0\). Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space.
- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as \(3=0\). Graphically, a system with no solution is represented by three planes with no point in common.

Figure \(\PageIndex{2}\): (a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.

Figure \(\PageIndex{3}\): All three figures represent three-by-three systems with no solution. (a) The three planes intersect with each other, but not at a common point. (b) Two of the planes are parallel and intersect with the third plane, but not with each other. (c) All three planes are parallel, so there is no point of intersection.
Example \(\PageIndex{1}\): Determining Whether an Ordered Triple Is a Solution to a System
Determine whether the ordered triple \((3,−2,1)\) is a solution to the system.
\[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]
Solution
We will check each equation by substituting in the values of the ordered triple for \( x,y\), and \(z\).
\[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1)=2 \nonumber \\[4pt] \text{True}} & {6x−4y+5z=31 \nonumber \\[4pt] 6(3)−4(−2)+5(1)=31 \nonumber \\[4pt] 18+8+5=31 \nonumber \\[4pt] \text{True} } & { 5x+2y+2z = 13 \nonumber \\[4pt] 5(3)+2(−2)+2(1)=13 \nonumber \\[4pt] 15−4+2=13 \nonumber \\[4pt] \text{True}} \end{array}\]
The ordered triple \((3,−2,1)\) is indeed a solution to the system.
How to: Given a linear system of three equations, solve for three unknowns
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Example \(\PageIndex{2}\): Solving a System of Three Equations in Three Variables by Elimination
Find a solution to the following system:
\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \nonumber \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]
Solution
There will always be several choices as to where to begin, but the most obvious first step here is to eliminate \(x\) by adding equations (1) and (2).
\[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(4) \nonumber \end{align} \nonumber\]
The second step is multiplying equation (1) by \(−2\) and adding the result to equation (3). These two steps will eliminate the variable \(x\).
\[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ multiplied by }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]
In equations (4) and (5), we have created a new two-by-two system. We can solve for \(z\) by adding the two equations.
\[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \nonumber \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]
Choosing one equation from each new system, we obtain the upper triangular form:
\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \nonumber \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]
Next, we back-substitute \(z=2\) into equation (4) and solve for \(y\).
\[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]
Finally, we can back-substitute \(z=2\) and \(y=−1\) into equation (1). This will yield the solution for \(x\).
\[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]
The solution is the ordered triple \((1,−1,2)\). See Figure \(\PageIndex{4}\).
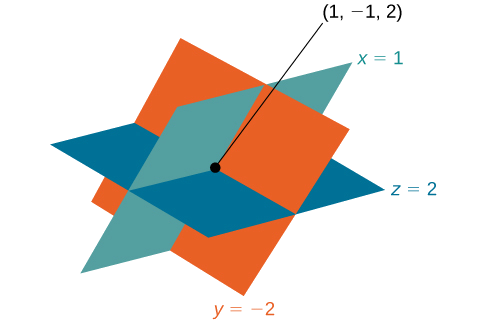
Figure \(\PageIndex{4}\)
Example \(\PageIndex{3}\): Solving a Real-World Problem Using a System of Three Equations in Three Variables
In the problem posed at the beginning of the section, John invested his inheritance of \($12,000\) in three different funds: part in a money-market fund paying \(3\%\) interest annually; part in municipal bonds paying \(4\%\) annually; and the rest in mutual funds paying \(7\%\) annually. John invested \($4,000\) more in mutual funds than he invested in municipal bonds. The total interest earned in one year was \($670\). How much did he invest in each type of fund?
Solution
To solve this problem, we use all of the information given and set up three equations. First, we assign a variable to each of the three investment amounts:
\[\begin{align} x &= \text{amount invested in money-market fund} \nonumber \\[4pt] y &= \text{amount invested in municipal bonds} \nonumber \\[4pt] z &= \text{amount invested in mutual funds} \nonumber \end{align} \nonumber\]
The first equation indicates that the sum of the three principal amounts is \($12,000\).
\[x+y+z=12,000 \nonumber\]
We form the second equation according to the information that John invested \($4,000\) more in mutual funds than he invested in municipal bonds.
\[z=y+4,000 \nonumber\]
The third equation shows that the total amount of interest earned from each fund equals \($670\).
\[0.03x+0.04y+0.07z=670 \nonumber\]
Then, we write the three equations as a system.
\[\begin{align} x+y+z &=12,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \\[4pt] 0.03x+0.04y+0.07z &= 670 \nonumber \end{align} \nonumber\]
To make the calculations simpler, we can multiply the third equation by \(100\). Thus,
\[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4,000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67,000 \; &(3) \nonumber \end{align} \nonumber\]
Step 1. Interchange equation (2) and equation (3) so that the two equations with three variables will line up.
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] 3x+4y+7z &= 67,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]
Step 2. Multiply equation (1) by \(−3\) and add to equation (2). Write the result as row 2.
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]
Step 3. Add equation (2) to equation (3) and write the result as equation (3).
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] 5z &= 35,000 \nonumber \end{align} \nonumber\]
Step 4. Solve for \(z\) in equation (3). Back-substitute that value in equation (2) and solve for \(y\). Then, back-substitute the values for \(z\) and \(y\) into equation (1) and solve for \(x\).
\[\begin{align} 5z &= 35,000 \nonumber \\[4pt] z &= 7,000 \nonumber \\[4pt] \nonumber \\[4pt] y+4(7,000) &= 31,000 \nonumber \\[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber\]
John invested \($2,000\) in a money-market fund, \($3,000\) in municipal bonds, and \($7,000\) in mutual funds.
Exercise \(\PageIndex{1}\)
Solve the system of equations in three variables.
\[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]
- Answer
-
\((1,−1,1)\)
Identifying Inconsistent Systems of Equations Containing Three Variables
Just as with systems of equations in two variables, we may come across an inconsistent system of equations in three variables, which means that it does not have a solution that satisfies all three equations. The equations could represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location. The process of elimination will result in a false statement, such as \(3=7\) or some other contradiction.
Example \(\PageIndex{4}\): Solving an Inconsistent System of Three Equations in Three Variables
Solve the following system.
\[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+13z &=8 \label{4.3} \end{align} \nonumber\]
Solution
Looking at the coefficients of \(x\), we can see that we can eliminate \(x\) by adding Equation \ref{4.1} to Equation \ref{4.2}.
\[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]
Next, we multiply equation (1) by \(−5\) and add it to equation (3).
\[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{multiplied by }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \end{align} \nonumber\]
Then, we multiply equation (4) by 2 and add it to equation (5).
\[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{multiplied by }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]
The final equation \(0=2\) is a contradiction, so we conclude that the system of equations in inconsistent and, therefore, has no solution.
Analysis
In this system, each plane intersects the other two, but not at the same location. Therefore, the system is inconsistent.
Exercise \(\PageIndex{2}\)
Solve the system of three equations in three variables.
\[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{align} \nonumber\]
- Answer
-
No solution.
Expressing the Solution of a System of Dependent Equations Containing Three Variables
We know from working with systems of equations in two variables that a dependent system of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the same, so that a solution to one equation will be the solution to the other two equations. All three equations could be different but they intersect on a line, which has infinite solutions. Or two of the equations could be the same and intersect the third on a line.
Example \(\PageIndex{5}\): Finding the Solution to a Dependent System of Equations
Find the solution to the given system of three equations in three variables.
\[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y+z &= 0 &(3) \nonumber \end{align} \nonumber\]
Solution
First, we can multiply equation (1) by \(−2\) and add it to equation (2).
\[\begin{align} −4x−2y+6z =0 & (1) \;\;\;\;\; \text{multiplied by }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\]
We do not need to proceed any further. The result we get is an identity, \(0=0\), which tells us that this system has an infinite number of solutions. There are other ways to begin to solve this system, such as multiplying equation (3) by \(−2\), and adding it to equation (1). We then perform the same steps as above and find the same result, \(0=0\).
When a system is dependent, we can find general expressions for the solutions. Adding equations (1) and (3), we have
\[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align} \nonumber\]
We then solve the resulting equation for \(z\).
\[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]
We back-substitute the expression for \(z\) into one of the equations and solve for \(y\).
\[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]
So the general solution is \(\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)\). In this solution, \(x\) can be any real number. The values of \(y\) and \(z\) are dependent on the value selected for \(x\).
Analysis
As shown in Figure \(\PageIndex{5}\), two of the planes are the same and they intersect the third plane on a line. The solution set is infinite, as all points along the intersection line will satisfy all three equations.

Figure \(\PageIndex{5}\)
Q&A: Does the generic solution to a dependent system always have to be written in terms of \(x\)?
No, you can write the generic solution in terms of any of the variables, but it is common to write it in terms of \(x\) and if needed \(x\) and \(y\).
Exercise \(\PageIndex{3}\):
Solve the following system.
\[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \end{align} \nonumber\]
- Answer
-
Infinite number of solutions of the form \((x,4x−11,−5x+18)\).
Media
Access these online resources for additional instruction and practice with systems of equations in three variables.
Key Concepts
- A solution set is an ordered triple {(x,y,z)} that represents the intersection of three planes in space. See Example \(\PageIndex{1}\).
- A system of three equations in three variables can be solved by using a series of steps that forces a variable to be eliminated. The steps include interchanging the order of equations, multiplying both sides of an equation by a nonzero constant, and adding a nonzero multiple of one equation to another equation. See Example \(\PageIndex{2}\).
- Systems of three equations in three variables are useful for solving many different types of real-world problems. See Example \(\PageIndex{3}\).
- A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the result is a contradiction. See Example \(\PageIndex{4}\).
- Systems of equations in three variables that are inconsistent could result from three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location.
- A system of equations in three variables is dependent if it has an infinite number of solutions. After performing elimination operations, the result is an identity. See Example \(\PageIndex{5}\).
- Systems of equations in three variables that are dependent could result from three identical planes, three planes intersecting at a line, or two identical planes that intersect the third on a line.
Contributors
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


