9.5: Matrices and Matrix Operations
- Last updated
- Save as PDF
- Page ID
- 1387
Learning Objectives
- Find the sum and difference of two matrices.
- Find scalar multiples of a matrix.
- Find the product of two matrices.
Two club soccer teams, the Wildcats and the Mud Cats, are hoping to obtain new equipment for an upcoming season. Table \(\PageIndex{1}\) shows the needs of both teams.
| Wildcats | Mud Cats | |
|---|---|---|
| Goals | 6 | 10 |
| Balls | 30 | 24 |
| Jerseys | 14 | 20 |
A goal costs \($300\); a ball costs \($10\); and a jersey costs \($30\). How can we find the total cost for the equipment needed for each team? In this section, we discover a method in which the data in the soccer equipment table can be displayed and used for calculating other information. Then, we will be able to calculate the cost of the equipment.

Finding the Sum and Difference of Two Matrices
To solve a problem like the one described for the soccer teams, we can use a matrix, which is a rectangular array of numbers. A row in a matrix is a set of numbers that are aligned horizontally. A column in a matrix is a set of numbers that are aligned vertically. Each number is an entry, sometimes called an element, of the matrix. Matrices (plural) are enclosed in [ ] or ( ), and are usually named with capital letters. For example, three matrices named \(A\), \(B\), and \(C\) are shown below.
\[ \begin{align*} A&=\begin{bmatrix} 1& 2 \\ 3 & 4 \\ \end{bmatrix} \\[4pt] B &=\begin{bmatrix} 1 & 2 & 7 \\ 0 & -5 & 6 \\ 7 & 8 & 2 \end{bmatrix} \\[4pt] C &=\begin{bmatrix} -1 & 3 \\ 0 & 2 \\ 3 & 1 \end{bmatrix} \end{align*}\]
A matrix is often referred to by its size or dimensions: \(m×n\) indicating \(m\) rows and \(n\) columns. Matrix entries are defined first by row and then by column. For example, to locate the entry in matrix \(A\) identified as \(a_{ij}\),we look for the entry in row \(i\),column \(j\). In matrix \(A\), shown below, the entry in row \(2\), column \(3\) is \(a_{23}\).
\[A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix} \nonumber\]
- A square matrix is a matrix with dimensions \(n × n\), meaning that it has the same number of rows as columns. The \(3×3\) matrix above is an example of a square matrix.
- A row matrix is a matrix consisting of one row with dimensions \(1 × n\). \[\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix} \nonumber\]
- A column matrix is a matrix consisting of one column with dimensions \(m × 1\). \[\begin{bmatrix} a_{11} \\ a_{21} \\a_{31} \end{bmatrix} \nonumber\]
A matrix may be used to represent a system of equations. In these cases, the numbers represent the coefficients of the variables in the system. Matrices often make solving systems of equations easier because they are not encumbered with variables. We will investigate this idea further in the next section, but first we will look at basic matrix operations.
Definition: MATRICES
A matrix is a rectangular array of numbers that is usually named by a capital letter: \(A\), \(B\), \(C\),and so on. Each entry in a matrix is referred to as \(a_{ij}\),such that \(i\) represents the row and \(j\) represents the column. Matrices are often referred to by their dimensions: \(m × n\) indicating \(m\) rows and \(n\) columns.
Example \(\PageIndex{1}\): Finding the Dimensions of the Given Matrix and Locating Entries
Given matrix \(A\):
- What are the dimensions of matrix \(A\)?
- What are the entries at \(a_{31}\) and \(a_{22}\)?
\[A=\begin{bmatrix} 2 & 1 & 0\\2 & 4 & 7\\3 & 1 & −2 \end{bmatrix} \nonumber\]
Solution
- The dimensions are \(3 \times 3\) because there are three rows and three columns.
- Entry \(a_{31}\) is the number at row 3, column 1, which is \(3\). The entry \(a_{22}\) is the number at row 2, column 2, which is \(4\). Remember, the row comes first, then the column.
Adding and Subtracting Matrices
We use matrices to list data or to represent systems. Because the entries are numbers, we can perform operations on matrices. We add or subtract matrices by adding or subtracting corresponding entries. To do this, the entries must correspond. Therefore, addition and subtraction of matrices is only possible when the matrices have the same dimensions. We can add or subtract a \(3 \times 3\) matrix and another \(3 \times 3\) matrix, but we cannot add or subtract a \(2 \times 3\) matrix and a \(3 \times 3\) matrix because some entries in one matrix will not have a corresponding entry in the other matrix.
ADDING AND SUBTRACTING MATRICES
Given matrices \(A\) and \(B\) of like dimensions, addition and subtraction of \(A\) and \(B\) will produce matrix \(C\) or matrix \(D\) of the same dimension.
\[A+B=C\]
such that \(a_{ij}+b_{ij}=c_{ij}\)
\[A−B=D\]
such that \(a_{ij}−b_{ij}=d_{ij}\)
Matrix addition is commutative.
\[A+B=B+A\]
It is also associative.
\[(A+B)+C=A+(B+C)\]
Example \(\PageIndex{2A}\): Finding the Sum of Matrices
Find the sum of \(A\) and \(B\), given
\[A=\begin{bmatrix}a & b\\c & d \end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber\]
Solution
Add corresponding entries.
\[\begin{align} A+B &=\begin{bmatrix}a & b\\c & d\end{bmatrix}+\begin{bmatrix}e & f\\g & h\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}a+e & b+f\\c+g & d+h \end{bmatrix} \nonumber \end{align} \nonumber\]
Example \(\PageIndex{2B}\): Adding Matrix \(A\) and Matrix \(B\)
Find the sum of \(A\) and \(B\).
\[A=\begin{bmatrix}4 &1\\3 & 2 \end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}5 & 9\\0 & 7\end{bmatrix} \nonumber\]
Solution
Add corresponding entries. Add the entry in row 1, column 1, \(a_{11}\), of matrix \(A\) to the entry in row 1, column 1, \(b_{11}\), of \(B\). Continue the pattern until all entries have been added.
\[\begin{align} A+B &=\begin{bmatrix}4&1\\3 &2\end{bmatrix}+\begin{bmatrix}5&9\\0&7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}4+5&1+9\\3+0&2+7\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}9&10\\3&9\end{bmatrix} \nonumber \end{align} \nonumber\]
Example \(\PageIndex{2C}\): Finding the Difference of Two Matrices
Find the difference of \(A\) and \(B\).
\(A=\begin{bmatrix}−2&3\\0&1\end{bmatrix}\) and \(B=\begin{bmatrix}8&1\\5&4\end{bmatrix}\)
Solution
We subtract the corresponding entries of each matrix.
\[\begin{align} A−B &=\begin{bmatrix}−2&3\\0&1\end{bmatrix}−\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−2−8&3−1\\0−5&1−4\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−10&2\\−5&−3\end{bmatrix} \nonumber \end{align} \nonumber\]
Example \(\PageIndex{2D}\): Finding the Sum and Difference of Two 3 x 3 Matrices
Given \(A\) and \(B\):
- Find the sum.
- Find the difference.
\[A=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber\]
Solution
- Add the corresponding entries.
\[\begin{align} A+B & =\begin{bmatrix} 2& −10& −2\\14 & 12 & 10\\4 & −2 & 2\end{bmatrix}+\begin{bmatrix}6 & 10 & −2\\0 & −12 & −4\\−5 & 2 & −2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+6 & −10+10 & −2−2\\14+0 & 12−12 & 10−4\\4−5 & −2+2 & 2−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix} 8 & 0 & −4\\14 & 0 & 6\\−1 & 0 & 0\end{bmatrix} \nonumber \end{align} \nonumber\]
- Subtract the corresponding entries.
\[\begin{align} A−B &=\begin{bmatrix}2&−10&−2\\14&12&10\\4&−2&2\end{bmatrix}−\begin{bmatrix}6&10&−2\\0&−12&−4\\−5&2&−2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2−6 & −10−10 & −2+2\\14−0 & 12+12 & 10+4\\4+5 & −2−2 & 2+2\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−4 & −20 & 0\\14 & 24 & 14\\9 & −4 & 4\end{bmatrix} \nonumber \end{align} \nonumber\]
Exercise \(\PageIndex{1}\)
Add matrix \(A\) and matrix \(B\).
\[A=\begin{bmatrix}2&6\\1&0\\1&−3\end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}3&−2\\1&5\\−4&3\end{bmatrix} \nonumber\]
- Answer
-
\[\begin{align} A+B&=\begin{bmatrix}2&6\\ 1 &0\\1&−3\end{bmatrix}+\begin{bmatrix} 3&-2 \\1&5 \\-4&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}2+3&6+(−2)\\1+1&0+5\\1+(-4)&−3+3\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}5&4\\2&5\\-3&0\end{bmatrix} \nonumber \end{align} \nonumber\]
Finding Scalar Multiples of a Matrix
Besides adding and subtracting whole matrices, there are many situations in which we need to multiply a matrix by a constant called a scalar. Recall that a scalar is a real number quantity that has magnitude, but not direction. For example, time, temperature, and distance are scalar quantities. The process of scalar multiplication involves multiplying each entry in a matrix by a scalar. A scalar multiple is any entry of a matrix that results from scalar multiplication.
Consider a real-world scenario in which a university needs to add to its inventory of computers, computer tables, and chairs in two of the campus labs due to increased enrollment. They estimate that \(15%\) more equipment is needed in both labs. The school’s current inventory is displayed in Table \(\PageIndex{2}\).
| Lab A | Lab B | |
|---|---|---|
| Computers | 15 | 27 |
| Computer Tables | 16 | 34 |
| Chairs | 16 | 34 |
Converting the data to a matrix, we have
\[C_{2013}=\begin{bmatrix}15 & 27\\16&34\\16&34\end{bmatrix} \nonumber\]
To calculate how much computer equipment will be needed, we multiply all entries in matrix \(C\) by \(0.15\).
\[(0.15)C_{2013}=\begin{bmatrix}(0.15)15&(0.15)27\\(0.15)16&(0.15)34\\(0.15)16 &(0.15)34\end{bmatrix}=\begin{bmatrix}2.25 &4.05\\2.4&5.1\\2.4&5.1\end{bmatrix} \nonumber\]
We must round up to the next integer, so the amount of new equipment needed is
\[\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix} \nonumber\]
Adding the two matrices as shown below, we see the new inventory amounts.
\[\begin{bmatrix}15&27\\16&34\\16&34\end{bmatrix}+\begin{bmatrix}3&5\\3&6\\3&6\end{bmatrix}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
This means
\[C_{2014}=\begin{bmatrix}18&32\\19&40\\19&40\end{bmatrix} \nonumber\]
Thus, Lab A will have \(18\) computers, \(19\) computer tables, and \(19\) chairs; Lab B will have \(32\) computers, \(40\) computer tables, and \(40\) chairs.
SCALAR MULTIPLICATION
Scalar multiplication involves finding the product of a constant by each entry in the matrix. Given
\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
the scalar multiple \(cA\) is
\[cA=c\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \nonumber\]
\[=\begin{bmatrix}ca_{11}&ca_{12}\\ca_{21}&ca_{22}\end{bmatrix} \nonumber\]
Scalar multiplication is distributive. For the matrices \(A\), \(B\),and \(C\) with scalars \(a\) and \(b\),
\[a(A+B)=aA+aB\]
\[(a+b)A=aA+bA\]
Example \(\PageIndex{3}\): Multiplying the Matrix by a Scalar
Multiply matrix \(A\) by the scalar \(3\).
\[A=\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber\]
Solution
Multiply each entry in \(A\) by the scalar \(3\).
\[ \begin{align} 3A&=3\begin{bmatrix}8&1\\5&4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3⋅8&3⋅1\\3⋅5&3⋅4\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}24&3\\15&12\end{bmatrix} \nonumber \end{align} \nonumber\]
Exercise \(\PageIndex{2}\)
Given matrix \(B\), find \(−2B\) where
\[B=\begin{bmatrix}4&1\\3&2\end{bmatrix} \nonumber\]
- Answer
-
\[−2B=\begin{bmatrix}−8&−2\\−6&−4\end{bmatrix} \nonumber\]
Example \(\PageIndex{4}\): Finding the Sum of Scalar Multiples
Find the sum \(3A+2B\).
\[A=\begin{bmatrix}1&−2&0\\0&−1&2\\4&3&−6\end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}−1&2&1\\0&−3&2\\0&1&−4\end{bmatrix} \nonumber\]
Solution
First, find \(3A\), then \(2B\).
\[ \begin{align} 3A&=\begin{bmatrix}3⋅1&3(−2)&3⋅0\\3⋅0&3(−1)&3⋅2\\3⋅4&3⋅3&3(−6)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}\nonumber \end{align} \nonumber\]
\[ \begin{align} 2B&=\begin{bmatrix}2(−1)&2⋅2&2⋅1\\2⋅0&2(−3)&2⋅2\\2⋅0&2⋅1&2(−4)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix}\nonumber \end{align} \nonumber\]
Now, add \(3A+2B\).
\[ \begin{align} 3A+2B&=\begin{bmatrix}3&−6&0\\0&−3&6\\12&9&−18\end{bmatrix}+\begin{bmatrix}−2&4&2\\0&−6&4\\0&2&−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}3−2&−6+4&0+2\\0+0&−3−6&6+4\\12+0&9+2&−18−8\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1& −2&2\\0&−9&10\\12&11&−26\end{bmatrix} \nonumber \end{align} \nonumber\]
Finding the Product of Two Matrices
In addition to multiplying a matrix by a scalar, we can multiply two matrices. Finding the product of two matrices is only possible when the inner dimensions are the same, meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. If \(A\) is an \(m × r\) matrix and \(B\) is an \(r × n\) matrix, then the product matrix \(AB\) is an \(m × n\) matrix. For example, the product \(AB\) is possible because the number of columns in \(A\) is the same as the number of rows in \(B\). If the inner dimensions do not match, the product is not defined.
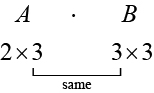
We multiply entries of \(A\) with entries of \(B\) according to a specific pattern as outlined below. The process of matrix multiplication becomes clearer when working a problem with real numbers.
To obtain the entries in row \(i\) of \(AB\), we multiply the entries in row \(i\) of \(A\) by column \(j\) in \(B\) and add. For example, given matrices \(A\) and \(B\), where the dimensions of \(A\) are \(2 \times 3\) and the dimensions of \(B\) are \(3 \times 3\),the product of \(AB\) will be a \(2 \times 3\) matrix.
\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{bmatrix} \nonumber \]
and
\[B=\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix} \nonumber\]
Multiply and add as follows to obtain the first entry of the product matrix \(AB\).
- To obtain the entry in row 1, column 1 of \(AB\),multiply the first row in \(A\) by the first column in \(B\),and add.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}=a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} \nonumber \]
- To obtain the entry in row 1, column 2 of \(AB\),multiply the first row of \(A\) by the second column in \(B\),and add.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{12}\\b_{22}\\b_{32}\end{bmatrix}=a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32} \nonumber \]
- To obtain the entry in row 1, column 3 of \(AB\),multiply the first row of \(A\) by the third column in \(B\),and add.
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\end{bmatrix} ⋅\begin{bmatrix}b_{13}\\b_{23}\\b_{33}\end{bmatrix}=a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \nonumber \]
We proceed the same way to obtain the second row of \(AB\). In other words, row 2 of \(A\) times column 1 of \(B\); row 2 of \(A\) times column 2 of \(B\); row 2 of \(A\) times column 3 of \(B\). When complete, the product matrix will be
\[AB=\begin{bmatrix}a_{11}⋅b_{11}+a_{12}⋅b_{21}+a_{13}⋅b_{31} &a_{11}⋅b_{12}+a_{12}⋅b_{22}+a_{13}⋅b_{32}&a_{11}⋅b_{13}+a_{12}⋅b_{23}+a_{13}⋅b_{33} \\a_{21}⋅b_{11}+a_{22}⋅b_{21}+a_{23}⋅b_{31}&a_{21}⋅b_{12}+a_{22}⋅b_{22}+a_{23}⋅b_{32}&a_{21}⋅b_{13}+a_{22}⋅b_{23}+a_{23}⋅b_{33}\end{bmatrix} \nonumber\]
PROPERTIES OF MATRIX MULTIPLICATION
For the matrice \(A, B\),and \(C\) the following properties hold.
- Matrix multiplication is associative: \[(AB)C=A(BC).\]
- Matrix multiplication is distributive: \[C(A+B)=CA+CB\] \[(A+B)C=AC+BC.\]
Note that matrix multiplication is not commutative.
Example \(\PageIndex{5A}\): Multiplying Two Matrices
Multiply matrix \(A\) and matrix \(B\).
\[A=\begin{bmatrix}1&2\\3&4\end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}5&6\\7&8\end{bmatrix} \nonumber\]
Solution
First, we check the dimensions of the matrices. Matrix \(A\) has dimensions \(2 × 2\) and matrix \(B\) has dimensions \(2 × 2\). The inner dimensions are the same so we can perform the multiplication. The product will have the dimensions \(2 × 2\).
We perform the operations outlined previously.
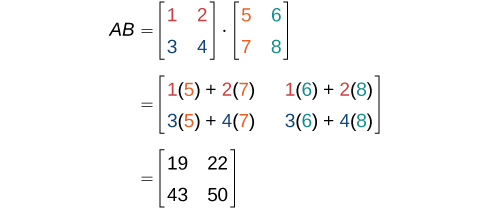
Example \(\PageIndex{5B}\): Multiplying Two Matrices
Given \(A\) and \(B\):
- Find \(AB\).
- Find \(BA\).
\[A=\begin{bmatrix}−1&2&3\\ 4&0&5\end{bmatrix} \nonumber\]
and
\[B=\begin{bmatrix}5&−1\\-4&0\\2&3\end{bmatrix} \nonumber\]
Solution
- As the dimensions of \(A\) are \(2 \times 3\) and the dimensions of \(B\) are \(3 \times 2\),these matrices can be multiplied together because the number of columns in \(A\) matches the number of rows in \(B\). The resulting product will be a \(2 \times 2\) matrix, the number of rows in \(A\) by the number of columns in \(B\).
\[ \begin{align}AB&=\begin{bmatrix}−1&2&3\\4&0&5\end{bmatrix} \begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−1(5)+2(−4)+3(2)&−1(−1)+2(0)+3(3)\\4(5)+0(−4)+5(2)&4(−1)+0(0)+5(3)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−7&10\\30&11\end{bmatrix} \nonumber \end{align} \nonumber\]
- The dimensions of \(B\) are \(3 \times 2\) and the dimensions of \(A\) are \(2 \times 3\). The inner dimensions match so the product is defined and will be a \(3 \times 3\) matrix.
\[ \begin{align}BA&=\begin{bmatrix}5&−1\\−4&0\\2&3\end{bmatrix} \begin{bmatrix} −1&2&3\\4&0&5\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}5(−1)+−1(4)&5(2)+−1(0)&5(3)+−1(5)\\−4(−1)+0(4)&−4(2)+0(0)&−4(3)+0(5)\\2(−1)+3(4)& 2(2)+3(0)&2(3)+3(5)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix} \nonumber \end{align} \nonumber\]
Analysis
Notice that the products \(AB\) and \(BA\) are not equal.
\[AB=\begin{bmatrix}−7&10\\30&11\end{bmatrix}≠ \begin{bmatrix}−9&10&10\\4&−8&−12\\10&4&21\end{bmatrix}=BA \nonumber\]
This illustrates the fact that matrix multiplication is not commutative.
Q&A: Is it possible for AB to be defined but not BA?
Yes, consider a matrix \(A\) with dimension \(3 × 4\) and matrix \(B\) with dimension \(4 × 2\). For the product \(AB\) the inner dimensions are \(4\) and the product is defined, but for the product \(BA\) the inner dimensions are \(2\) and \(3\) so the product is undefined.
Example \(\PageIndex{6}\): Using Matrices in Real-World Problems
Let’s return to the problem presented at the opening of this section. We have Table \(\PageIndex{3}\), representing the equipment needs of two soccer teams.
| Wildcats | Mud Cats | |
|---|---|---|
| Goals | 6 | 10 |
| Balls | 30 | 24 |
| Jerseys | 14 | 20 |
We are also given the prices of the equipment, as shown in Table \(\PageIndex{4}\).
| Goal | $300 |
| Ball | $10 |
| Jersey | $30 |
We will convert the data to matrices. Thus, the equipment need matrix is written as
\[E=\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber\]
The cost matrix is written as
\[C=\begin{bmatrix}300&10&30\end{bmatrix} \nonumber\]
We perform matrix multiplication to obtain costs for the equipment.
\[ \begin{align} CE&=\begin{bmatrix}300&10&30\end{bmatrix}⋅\begin{bmatrix}6&10\\30&24\\14&20\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}300(6)+10(30)+30(14)&300(10)+10(24)+30(20)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}2,520&3,840\end{bmatrix} \nonumber \end{align} \nonumber\]
The total cost for equipment for the Wildcats is \($2,520\), and the total cost for equipment for the Mud Cats is \($3,840\).
How to: Given a matrix operation, evaluate using a calculator
- Save each matrix as a matrix variable \([A], [B], [C],...\)
- Enter the operation into the calculator, calling up each matrix variable as needed.
- If the operation is defined, the calculator will present the solution matrix; if the operation is undefined, it will display an error message.
Example \(\PageIndex{7}\): Using a Calculator to Perform Matrix Operations
Find \(AB−C\) given
\(A=\begin{bmatrix}−15&25&32\\41&−7&−28\\10&34&−2\end{bmatrix}\), \(B=\begin{bmatrix}45&21&−37\\−24&52&19\\6&−48&−31\end{bmatrix}\), and \(C=\begin{bmatrix}−100&−89&−98\\25&−56&74\\−67&42&−75\end{bmatrix}\)
Solution
On the matrix page of the calculator, we enter matrix \(A\) above as the matrix variable \([ A ]\), matrix \(B\) above as the matrix variable \([ B ]\), and matrix \(C\) above as the matrix variable \([ C ]\).
On the home screen of the calculator, we type in the problem and call up each matrix variable as needed.
\[[A]×[B]−[C] \nonumber\]
The calculator gives us the following matrix.
\[\begin{bmatrix}−983&−462&136\\1,820&1,897&−856\\−311&2,032&413\end{bmatrix} \nonumber\]
Media
Access these online resources for additional instruction and practice with matrices and matrix operations.
Key Concepts
- A matrix is a rectangular array of numbers. Entries are arranged in rows and columns.
- The dimensions of a matrix refer to the number of rows and the number of columns. A \(3×2\) matrix has three rows and two columns. See Example \(\PageIndex{1}\).
- We add and subtract matrices of equal dimensions by adding and subtracting corresponding entries of each matrix. See Example \(\PageIndex{2}\), Example \(\PageIndex{3}\), Example \(\PageIndex{4}\), and Example \(\PageIndex{5}\).
- Scalar multiplication involves multiplying each entry in a matrix by a constant. See Example \(\PageIndex{6}\).
- Scalar multiplication is often required before addition or subtraction can occur. See Example \(\PageIndex{7}\).
- Multiplying matrices is possible when inner dimensions are the same—the number of columns in the first matrix must match the number of rows in the second.
- The product of two matrices, \(A\) and \(B\),is obtained by multiplying each entry in row 1 of \(A\) by each entry in column 1 of \(B\); then multiply each entry of row 1 of \(A\) by each entry in columns 2 of \(B\),and so on. See Example \(\PageIndex{8}\) and Example \(\PageIndex{9}\).
- Many real-world problems can often be solved using matrices. See Example \(\PageIndex{10}\).
- We can use a calculator to perform matrix operations after saving each matrix as a matrix variable. See Example \(\PageIndex{11}\).


