11.1: Sequences and Their Notations
- Last updated
- Save as PDF
- Page ID
- 1396
Learning Objectives
- Write the terms of a sequence defined by an explicit formula.
- Write the terms of a sequence defined by a recursive formula.
- Use factorial notation.
A video game company launches an exciting new advertising campaign. They predict the number of online visits to their website, or hits, will double each day. The model they are using shows \(2\) hits the first day, \(4\) hits the second day, \(8\) hits the third day, and so on (Table \(\PageIndex{1}\)).
| Day | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|
| Hits | 2 | 4 | 8 | 16 | 32 | … |
If their model continues, how many hits will there be at the end of the month? To answer this question, we’ll first need to know how to determine a list of numbers written in a specific order. In this section, we will explore these kinds of ordered lists.
Writing the Terms of a Sequence Defined by an Explicit Formula
One way to describe an ordered list of numbers is as a sequence. A sequence is a function whose domain is a subset of the counting numbers. The sequence established by the number of hits on the website is
\(\{ 2,4,8,16,32,…\}\)
The ellipsis (…) indicates that the sequence continues indefinitely. Each number in the sequence is called a term. The first five terms of this sequence are \(2\), \(4\), \(8\), \(16\), and \(32\).
Listing all of the terms for a sequence can be cumbersome. For example, finding the number of hits on the website at the end of the month would require listing out as many as \(31\) terms. A more efficient way to determine a specific term is by writing a formula to define the sequence.
One type of formula is an explicit formula, which defines the terms of a sequence using their position in the sequence. Explicit formulas are helpful if we want to find a specific term of a sequence without finding all of the previous terms. We can use the formula to find the nth term of the sequence, where nn is any positive number. In our example, each number in the sequence is double the previous number, so we can use powers of 2 to write a formula for the nth term.

The first term of the sequence is \(2^1=2\), the second term is \(2^2=4\), the third term is \(2^3=8\), and so on. The nth term of the sequence can be found by raising 2 to the nth power. An explicit formula for a sequence is named by a lower case letter \(a\), \(b\), \(c\)... with the subscript \(n\). The explicit formula for this sequence is
\(a_n=2^n\)
Now that we have a formula for the nth term of the sequence, we can answer the question posed at the beginning of this section. We were asked to find the number of hits at the end of the month, which we will take to be 31 days. To find the number of hits on the last day of the month, we need to find the 31st term of the sequence. We will substitute 31 for \(n\) in the formula.
\[ \begin{align*} a_{31}=2^{31} \\ [5pt] &=2,147,483,648 \end{align*}\]
If the doubling trend continues, the company will get \(2,147,483,648\) hits on the last day of the month. That is over \(2.1\) billion hits! The huge number is probably a little unrealistic because it does not take consumer interest and competition into account. It does, however, give the company a starting point from which to consider business decisions.
Another way to represent the sequence is by using a table. The first five terms of the sequence and the nth term of the sequence are shown in Table \(\PageIndex{2}\).
| \(n\) | 1 | 2 | 3 | 4 | 5 | \(n\) |
|---|---|---|---|---|---|---|
| \(n^{th}\) term of the sequence, \(a_n\) | 2 | 4 | 8 | 16 | 32 | \(2^n\) |
Graphing provides a visual representation of the sequence as a set of distinct points. We can see from the graph in Figure \(\PageIndex{1}\) that the number of hits is rising at an exponential rate. This particular sequence forms an exponential function.
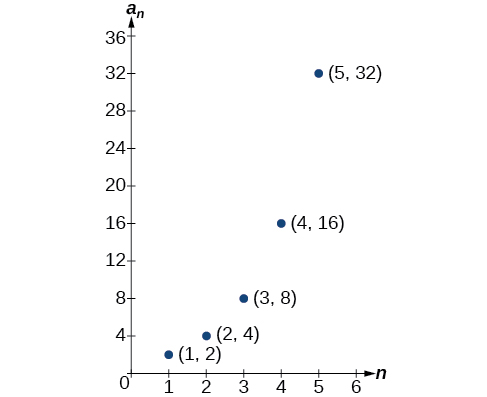
Figure \(\PageIndex{1}\)
Lastly, we can write this particular sequence as
\(\{2,4,8,16,32,…,2^n,…\}\)
A sequence that continues indefinitely is called an infinite sequence. The domain of an infinite sequence is the set of counting numbers. If we consider only the first \(10\) terms of the sequence, we could write
\(\{2,4,8,16,32,…,2^n,…,1024\}\)
This sequence is called a finite sequence because it does not continue indefinitely.
SEQUENCE
A sequence is a function whose domain is the set of positive integers. A finite sequence is a sequence whose domain consists of only the first \(n\) positive integers. The numbers in a sequence are called terms. The variable \(a\) with a number subscript is used to represent the terms in a sequence and to indicate the position of the term in the sequence.
\[a_1,a_2,a_3,…,a_n,…\]
We call \(a_1\) the first term of the sequence, \(a_2\) the second term of the sequence, \(a_3\) the third term of the sequence, and so on. The term \(a_n\) is called the nth term of the sequence, or the general term of the sequence. An explicit formula defines the nth term of a sequence using the position of the term. A sequence that continues indefinitely is an infinite sequence.
Q&A: Does a sequence always have to begin with \(a_1\)?
No. In certain problems, it may be useful to define the initial term as \(a_0\) instead of \(a_1\). In these problems, the domain of the function includes \(0\).
How to: Given an explicit formula, write the first \(n\) terms of a sequence
- Substitute each value of \(n\) into the formula. Begin with \(n=1\) to find the first term, \(a_1\).
- To find the second term, \(a_2\), use \(n=2\).
- Continue in the same manner until you have identified all nn terms.
Example \(\PageIndex{1}\): Writing the Terms of a Sequence Defined by an Explicit Formula
Write the first five terms of the sequence defined by the explicit formula \(a_n=−3n+8\).
Solution
Substitute \(n=1\) into the formula. Repeat with values \(2\) through \(5\) for \(n\).
\(\begin{array}{ll} n=1 & a_1=−3(1)+8=5 \\ n=2 & a_2=−3(2)+8=2 \\ n=3 & a_3=−3(3)+8=−1 \\ n=4 & a_4=−3(4)+8=−4 \\ n=5 & a_5=−3(5)+8=−7 \end{array}\)
The first five terms are \(\{5,2,−1,−4,−7\}\).
Analysis
The sequence values can be listed in a table. A table, such as Table \(\PageIndex{3}\), is a convenient way to input the function into a graphing utility.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(a_n\) | 5 | 2 | –1 | –4 | –7 |
A graph can be made from this table of values. From the graph in Figure \(\PageIndex{2}\), we can see that this sequence represents a linear function, but notice the graph is not continuous because the domain is over the positive integers only.

Figure \(\PageIndex{2}\)
Exercise \(\PageIndex{1}\)
Write the first five terms of the sequence defined by the explicit formula \(t_n=5n−4\).
- Answer
-
The first five terms are \(\{1,6, 11, 16, 21\}\).
Investigating Alternating Sequences
Sometimes sequences have terms that are alternate. In fact, the terms may actually alternate in sign. The steps to finding terms of the sequence are the same as if the signs did not alternate. However, the resulting terms will not show increase or decrease as \(n\) increases. Let’s take a look at the following sequence.
\(\{2,−4,6,−8\}\)
Notice the first term is greater than the second term, the second term is less than the third term, and the third term is greater than the fourth term. This trend continues forever. Do not rearrange the terms in numerical order to interpret the sequence.
How to: Given an explicit formula with alternating terms, write the first nn terms of a sequence
- Substitute each value of nn into the formula. Begin with \(n=1\) to find the first term, \(a_1\). The sign of the term is given by the \({(−1)}^n\) in the explicit formula.
- To find the second term, \(a_2\), use \(n=2\).
- Continue in the same manner until you have identified all \(n\) terms.
Example \(\PageIndex{2}\): Writing the Terms of an Alternating Sequence Defined by an Explicit Formula
Write the first five terms of the sequence.
\(a_n=\dfrac{{(−1)}^nn^2}{n+1}\)
Solution
Substitute \(n=1\), \(n=2\), and so on in the formula.
\(\begin{array}{ll} n=1 & a_1=\dfrac{{(−1)}^12^2}{1+1}=−\dfrac{1}{2} \\ n=2 & a_2=\dfrac{{(−1)}^22^2}{2+1}=\dfrac{4}{3} \\ n=3 & a_3=\dfrac{{(−1)}^33^2}{3+1}=−\dfrac{9}{4} \\ n=4 & a_4=\dfrac{{(−1)}^44^2}{4+1}=\dfrac{16}{5} \\ n=5 & a_5=\dfrac{{(−1)}^55^2}{5+1}=−\dfrac{25}{6} \end{array}\)
The first five terms are \(\{−12,43,−94,165,−256\}\).
Analysis
The graph of this function, shown in Figure \(\PageIndex{3}\), looks different from the ones we have seen previously in this section because the terms of the sequence alternate between positive and negative values.

Figure \(\PageIndex{3}\)
Q&A: In the example above, does the \((–1)\) to the power of \(n\) account for the oscillations of signs?
Yes, the power might be \(n\), \(n+1\), \(n−1\), and so on, but any odd powers will result in a negative term, and any even power will result in a positive term.
Exercise \(\PageIndex{2}\)
Write the first five terms of the sequence:
\(a_n=\dfrac{4n}{{(−2)}^n}\)
- Answer
-
The first five terms are \(\{−2, 2, −32, 1, −58\}\).
Investigating Piecewise Explicit Formulas
We’ve learned that sequences are functions whose domain is over the positive integers. This is true for other types of functions, including some piecewise functions. Recall that a piecewise function is a function defined by multiple subsections. A different formula might represent each individual subsection.
How to: Given an explicit formula for a piecewise function, write the first \(n\) terms of a sequence
- Identify the formula to which \(n=1\) applies.
- To find the first term, \(a_1\), use \(n=1\) in the appropriate formula.
- Identify the formula to which \(n=2\) applies.
- To find the second term, \(a_2\), use \(n=2\) in the appropriate formula.
- Continue in the same manner until you have identified all \(n\) terms.
Example \(\PageIndex{3}\): Writing the Terms of a Sequence Defined by a Piecewise Explicit Formula
Write the first six terms of the sequence.
\(a_n=\begin{cases}n^2\space \text{if n is not divisible by } 3\\\dfrac{n}{3} \text{if n is divisible by } 3\end{cases}\)
Solution
Substitute \(n=1\), \(n=2\), and so on in the appropriate formula. Use \(n^2\) when \(n\) is not a multiple of \(3\). Use \(n^3\) when \(n\) is a multiple of \(3\).
\(\begin{array}{ll} a_1=1^2=1 & 1 \text{ is not a multiple of }3. \text{ Use } n^2. \\ a_2=2^2=4 & 2 \text{ is not a multiple of }3 \text{ . Use }n^2. \\ a_3=\dfrac{3}{3}=1 & 3 \text{ is a multiple of }3 \text{. Use }\dfrac{n}{3}. \\ a_4=4^2=16 & 4 \text{ is not a multiple of }3. \text{ Use }n^2. \\ a_5=5^2=25 & 5 \text{ is not a multiple of } 3. \text{Use }n^2. \\ a_6=\dfrac{6}{3}=2 & 6 \text{ is a multiple of }3. \text{Use }\dfrac{n}{3} \end{array}\)
The first six terms are \(\{1, 4, 1, 16, 25, 2\}\).
Analysis
Every third point on the graph shown in Figure \(\PageIndex{4}\) stands out from the two nearby points. This occurs because the sequence was defined by a piecewise function.
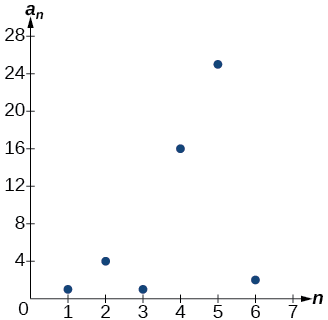
Figure \(\PageIndex{4}\)
Exercise \(\PageIndex{3}\)
Write the first six terms of the sequence.
\(a_n=\begin{cases}2n^3 \text{ if } n\text{ is odd} \\ \dfrac{5n}{2} \text{ if } n \text{ is even}\end{cases}\)
- Answer
-
The first six terms are \(\{2, 5, 54, 10, 250, 15\}\).
Finding an Explicit Formula
Thus far, we have been given the explicit formula and asked to find a number of terms of the sequence. Sometimes, the explicit formula for the nth term of a sequence is not given. Instead, we are given several terms from the sequence. When this happens, we can work in reverse to find an explicit formula from the first few terms of a sequence. The key to finding an explicit formula is to look for a pattern in the terms. Keep in mind that the pattern may involve alternating terms, formulas for numerators, formulas for denominators, exponents, or bases.
How to: Given the first few terms of a sequence, find an explicit formula for the sequence
- Look for a pattern among the terms.
- If the terms are fractions, look for a separate pattern among the numerators and denominators.
- Look for a pattern among the signs of the terms.
- Write a formula for \(a_n\) in terms of \(n\). Test your formula for \(n=1\), \(n=2\), and \(n=3\).
Example \(\PageIndex{4}\): Writing an Explicit Formula for the nth Term of a Sequence
Write an explicit formula for the nth term of each sequence.
- \(\{−\dfrac{2}{11}, \dfrac{3}{13}, −\dfrac{4}{15}, \dfrac{5}{17}, −\dfrac{6}{19},…\}\)
- \(\{−\dfrac{2}{25}, −\dfrac{2}{125}, −\dfrac{2}{625}, −\dfrac{2}{3,125}, −\dfrac{2}{15,625},…\}\)
- \(\{e^4,e^5,e^6,e^7,e^8,…\}\)
Solution
Look for the pattern in each sequence.
- The terms alternate between positive and negative. We can use \({(−1)}^n\) to make the terms alternate. The numerator can be represented by \(n+1\). The denominator can be represented by \(2n+9\).
\(a_n=\dfrac{{(−1)}^n(n+1)}{2n+9}\)
- The terms are all negative.
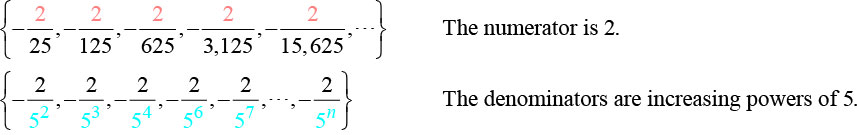
So we know that the fraction is negative, the numerator is \(2\), and the denominator can be represented by \(5n+1\).
\(a_n=−\dfrac{2}{5^{n+1}}\)
- The terms are powers of \(e\). For \(n=1\), the first term is \(e^4\) so the exponent must be \(n+3\).
\(a_n=e^{n+3}\)
Exercise \(\PageIndex{4A}\)
Write an explicit formula for the nth term of the sequence.\(\{9,−81,729,−6,561,59,049,…\}\)
- Answer
-
\(a_n={(−1)}^{n+1}9^n\)
Exercise \(\PageIndex{4B}\)
Write an explicit formula for the nth term of the sequence.
\(\{−34,−98,−2712,−8116,−24320,...\}\)
- Answer
-
\(a_n=−\dfrac{3^n}{4n}\)
Exercise \(\PageIndex{4C}\)
Write an explicit formula for the nth term of the sequence.
\(\left \{ \dfrac{1}{e^2}, \dfrac{1}{e}, 1, e, e^2,... \right \}\)
- Answer
-
\(a_n=e^{n−3}\)
Writing the Terms of a Sequence Defined by a Recursive Formula
Sequences occur naturally in the growth patterns of nautilus shells, pinecones, tree branches, and many other natural structures. We may see the sequence in the leaf or branch arrangement, the number of petals of a flower, or the pattern of the chambers in a nautilus shell. Their growth follows the Fibonacci sequence, a famous sequence in which each term can be found by adding the preceding two terms. The numbers in the sequence are \(1, 1, 2, 3, 5, 8, 13, 21, 34,….\) Other examples from the natural world that exhibit the Fibonacci sequence are the Calla Lily, which has just one petal, the Black-Eyed Susan with \(13\) petals, and different varieties of daisies that may have \(21\) or \(34\) petals.
Each term of the Fibonacci sequence depends on the terms that come before it. The Fibonacci sequence cannot easily be written using an explicit formula. Instead, we describe the sequence using a recursive formula, a formula that defines the terms of a sequence using previous terms.
A recursive formula always has two parts: the value of an initial term (or terms), and an equation defining \(a_n\) in terms of preceding terms. For example, suppose we know the following:
\[\begin{align*} a_1 &= 3 \\ a_n &= 2a_{n−1}−1 , \text{ for }n≥2 \end{align*}\]
We can find the subsequent terms of the sequence using the first term.
\[\begin{align*} a_1 &= 3 \\ a_2 &= 2a_1−1=2(3)−1=5 \\ a_3 &= 2a_2−1=2(5)−1=9 \\ a_4 &= 2a_3−1=2(9)−1=17 \end{align*}\]
So the first four terms of the sequence are \(\{3, 5, 9, 17\}\).
The recursive formula for the Fibonacci sequence states the first two terms and defines each successive term as the sum of the preceding two terms.
\[\begin{align*}a_1 &= 1 \\ a_2 &= 1 \\ a_n &= a_{n−1}+a_{n−2} \text{, for }n≥3 \end{align*}\]
To find the tenth term of the sequence, for example, we would need to add the eighth and ninth terms. We were told previously that the eighth and ninth terms are \(21\) and \(34\), so
\(a_{10}=a_9+a_8=34+21=55\)
RECURSIVE FORMULA
A recursive formula is a formula that defines each term of a sequence using preceding term(s). Recursive formulas must always state the initial term, or terms, of the sequence.
Q&A: Must the first two terms always be given in a recursive formula?
No. The Fibonacci sequence defines each term using the two preceding terms, but many recursive formulas define each term using only one preceding term. These sequences need only the first term to be defined.
How to: Given a recursive formula with only the first term provided, write the first n terms of a sequence
- Identify the initial term, \(a_1\), which is given as part of the formula. This is the first term.
- To find the second term, \(a_2\), substitute the initial term into the formula for \(a_{n−1}\). Solve.
- To find the third term, \(a_3\), substitute the second term into the formula. Solve.
- Repeat until you have solved for the nth term.
Example \(\PageIndex{5}\): Writing the Terms of a Sequence Defined by a Recursive Formula
Write the first five terms of the sequence defined by the recursive formula.
\[\begin{align*}a_1 &= 9 \\ a_n &= 3a_{n−1}−20 , \text{ for }n≥2 \end{align*}\]
Solution
The first term is given in the formula. For each subsequent term, we replace \(a_n−1\) with the value of the preceding term.
\(\begin{array}{ll} n=1 & a_1=9 \\ n=2 & a_2=3a_1−20=3(9)−20=27−20=7 \\ n=3 & a_3=3a_2−20=3(7)−20=21−20=1 \\ n=4 & a_4=3a_3−20=3(1)−20=3−20=−17 \\ n=5 & a_5=3a_4−20=3(−17)−20=−51−20=−71 \end{array}\)
The first five terms are \(\{9, 7, 1, –17, –71\}\). See Figure \(\PageIndex{5}\).
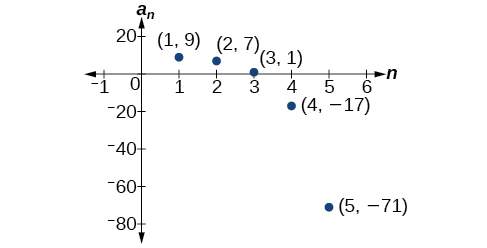
Figure \(\PageIndex{5}\)
Exercise \(\PageIndex{5}\)
Write the first five terms of the sequence defined by the recursive formula.
\[\begin{align*} a_1 &= 2 \\ a_n &= 2a_{n−1}+1 , \text{ for }n≥2 \end{align*}\]
- Answer
-
\(\{2, 5, 11, 23, 47\}\)
How to: Given a recursive formula with two initial terms, write the first \(n\) terms of a sequence
- Identify the initial term, \(a_1\), which is given as part of the formula.
- Identify the second term, \(a_2\), which is given as part of the formula.
- To find the third term, substitute the initial term and the second term into the formula. Evaluate.
- Repeat until you have evaluated the nth term.
Example \(\PageIndex{6}\): Writing the Terms of a Sequence Defined by a Recursive Formula
Write the first six terms of the sequence defined by the recursive formula.
\[\begin{align*} a_1 &=1 \\ a_2 &= 2 \\ a_n &= 3a_{n−1}+4a_{n−2} , \text{ for }n≥3 \end{align*}\]
Solution
The first two terms are given. For each subsequent term, we replace \(a_{n−1}\) and \(a_{n−2}\) with the values of the two preceding terms.
\(\begin{array}{ll} n=3 & a_3=3a_2+4a_1=3(2)+4(1)=10 \\ n=4 & a_4=3a_3+4a_2=3(10)+4(2)=38 \\ n=5 & a_5=3a_4+4a_3=3(38)+4(10)=154 \\ n=6 & a_6=3a_5+4a_4=3(154)+4(38)=614 \end{array}\)
The first six terms are \(\{1,2,10,38,154,614\}\). See Figure \(\PageIndex{6}\).
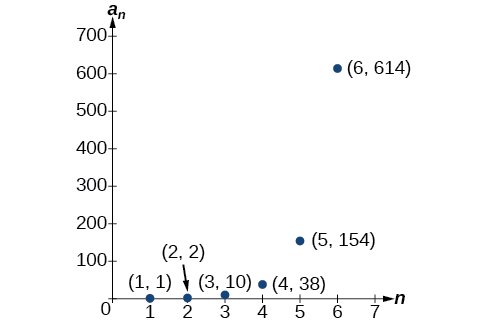
Figure \(\PageIndex{6}\)
Exercise \(\PageIndex{6}\)
Write the first \(8\) terms of the sequence defined by the recursive formula.
\[\begin{align*}a_1 &= 0 \\ a_2 &= 1 \\ a_3 &= 1 \\ a_n &= \dfrac{a_{n−1}}{a_{n−2}}+a_{n−3} , \text{ for }n≥4 \end{align*}\]
- Answer
-
\(\left \{0, 1, 1, 1, 2, 3, 52, 176 \right \}\).
Using Factorial Notation
The formulas for some sequences include products of consecutive positive integers. \(n\) factorial, written as \(n!\), is the product of the positive integers from \(1\) to \(n\). For example,
\[\begin{align*}4! &= 4⋅3⋅2⋅1=24 \\ 5! &= 5⋅4⋅3⋅2⋅1=120 \end{align*}\]
An example of formula containing a factorial is \(a_n=(n+1)!\). The sixth term of the sequence can be found by substituting \(6\) for \(n\).
\(a_6=(6+1)!=7!=7·6·5·4·3·2·1=5040\)
The factorial of any whole number \(n\) is \(n(n−1)!\) We can therefore also think of \(5!\) as \(5⋅4!\).
FACTORIAL
\(n\) factorial is a mathematical operation that can be defined using a recursive formula. The factorial of \(n\), denoted \(n!\), is defined for a positive integer \(n\) as:
\[\begin{align} 0! &= 1 \\ 1! &= 1 \\ n! &= n(n−1)(n−2)⋯(2)(1), \text{ for }n≥2 \end{align}\]
The special case \(0!\) is defined as \(0!=1\).
Q&A: Can factorials always be found using a calculator?
No. Factorials get large very quickly—faster than even exponential functions! When the output gets too large for the calculator, it will not be able to calculate the factorial.
Example \(\PageIndex{7}\): Writing the Terms of a Sequence Using Factorials
Write the first five terms of the sequence defined by the explicit formula \(a_n=\dfrac{5n}{(n+2)!}\).
Solution
Substitute \(n=1\), \(n=2\), and so on in the formula.
\(\begin{array}{ll} n=1 & a_1=\dfrac{5(1)}{(1+2)!}=\dfrac{5}{3!}=\dfrac{5}{3·2·1}=\dfrac{5}{6} \\ n=2 & a_2=\dfrac{5(2)}{(2+2)!}=\dfrac{10}{4!}=\dfrac{10}{4·3·2·1}=\dfrac{5}{12} \\ n=3 & a_3=\dfrac{5(3)}{(3+2)!}=\dfrac{15}{5!}=\dfrac{15}{5·4·3·2·1}=\dfrac{1}{8} \\ n=4 & a_4=\dfrac{5(4)}{(4+2)!}=\dfrac{20}{6!}=\dfrac{20}{6·5·4·3·2·1}=\dfrac{1}{36} \\ n=5 & a_5=\dfrac{5(5)}{(5+2)!}=\dfrac{25}{7!}=\dfrac{25}{7·6·5·4·3·2·1}=\dfrac{5}{1,008} \end{array}\)
The first five terms are \(\left \{\dfrac{5}{6}, \dfrac{5}{12}, \dfrac{1}{8}, \dfrac{1}{36}, \dfrac{5}{1,008} \right \}\).
Analysis
Figure \(\PageIndex{7}\) shows the graph of the sequence. Notice that, since factorials grow very quickly, the presence of the factorial term in the denominator results in the denominator becoming much larger than the numerator as nn increases. This means the quotient gets smaller and, as the plot of the terms shows, the terms are decreasing and nearing zero.
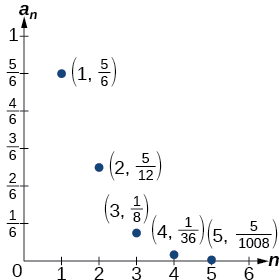
Figure \(\PageIndex{7}\)
Exercise \(\PageIndex{7}\)
Write the first five terms of the sequence defined by the explicit formula \(a_n=\dfrac{(n+1)!}{2n}\).
- Answer
-
The first five terms are \(\left \{1, \dfrac{3}{2}, 4, 15, 72 \right \}\).
Media
Access this online resource for additional instruction and practice with sequences.
Key Equations
| Formula for a factorial |
\(0!=1\) \(1!=1\) \(n!=n(n−1)(n−2)⋯(2)(1)\), for \(n≥2\) |
Key Concepts
- A sequence is a list of numbers, called terms, written in a specific order.
- Explicit formulas define each term of a sequence using the position of the term. See Example \(\PageIndex{1}\), Example \(\PageIndex{2}\), and Example \(\PageIndex{3}\).
- An explicit formula for thenth nth term of a sequence can be written by analyzing the pattern of several terms. See Example \(\PageIndex{4}\).
- Recursive formulas define each term of a sequence using previous terms.
- Recursive formulas must state the initial term, or terms, of a sequence.
- A set of terms can be written by using a recursive formula. See Example \(\PageIndex{5}\) and Example \(\PageIndex{6}\).
- A factorial is a mathematical operation that can be defined recursively.
- The factorial of \(n\) is the product of all integers from \(1\) to \(n\). See Example \(\PageIndex{7}\).
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


