2.2: The Commutative Property of Addition and Multiplication
- Page ID
- 13968
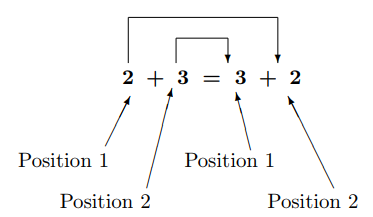
Figure 2.2.1
\(2\) commuted (traveled) from position 1 to position 2
and
\(3\) commuted (traveled) from position 2 to position 1.
Note
A commuter is a traveler. Do not say “communitive" property.
Figure 2.2.1 illustrates the commutative property of addition.
In general
\[\boxed{\Large a+b=b+a}\]
where \(a\) and \(b\) are any real numbers (like \(-6.4\), \(\displaystyle \frac{2}{7}\), \(\pi\)). Any real number can hide in the \(a\)-box or the \(b\)-box.
Example \(\PageIndex{1}\): Is subtraction commutative?
Is \(3-1=1-3\) a true statement?
Solution
No, because \(3-1-2\) and \(1-3=-2\). If we find one counterexample, one example that shows that subtraction is not commutative, the general property (using \(a\) and \(b\)) does not exist.
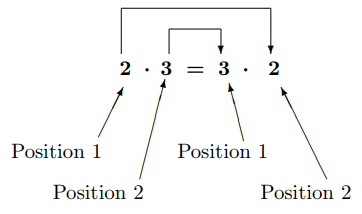
Figure 2.2.2
\(2\) commuted (traveled) from position 1 to position 2
and
\(3\) commuted (traveled) from position 2 to position 1.
Figure 2.2.2 illustrates the commutative property of multiplication.
In general
\[\boxed{\Large ab=ba}\]
where \(a\) and \(b\) are any real numbers (like \(-6.4\), \(\displaystyle \frac{2}{7}\), \(\pi\)). Any real number can hide in the \(a\)-box or the \(b\)-box.
Note that \(ab\) means \(a\) times \(b\).
Example \(\PageIndex{2}\): Is division commutative?
Is \(4\div 2=2\div 4\) a true statement?
Solution
No, because \(4\div 2=2\) and \(2\div 4=\displaystyle \frac{1}{2}=0.5\). If we find one counterexample, one example that shows that division is not commutative, the general property (using \(a\) and \(b\)) does not exist


