6.2: Informal introduction to functions

Last updated
Save as PDF

Page ID: 23907

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

You have seen many examples of functions in your previous math classes. Most of these were probably given by formulas (such as $f(x) = x^{3}$), but functions can also be given in other ways. The key property of a function is that it accepts inputs, and provides a corresponding output value for each possible input.

Example $6.2.1$.

For the function $f(x) = x^{3}$, the input $x$ can be any real number. Plugging a value for $x$ into the formula yields an output value, which is also a real number. For example, using $x = 2$ as the input yields the output value $f(2) = 2^{3} = 8$.

Definition $6.2.2$ (unofficial).

Suppose $f$ is any function.

The set of allowable inputs of $f$ is called the domain of $f$.
If $A$ is the domain of $f$, and $B$ is any set that contains all of the possible outputs of $f$, then we say that $f$ is a function from $A$ to $B$. In the case of the function $f(x) = x^{3}$, we may take $A$ and $B$ to both be the set of real numbers; thus, $f$ is a function from $\mathbb{R} to \mathbb{R}$.

Example $6.2.3$.

$g(x) = 1/x$ is not a function from $\mathbb{R}$ to $\mathbb{R}$. This is because 0 is an element of $\mathbb{R}$, but the formula does not define a value for $g(0)$. Thus, 0 cannot be in the domain of $g$. To correct this problem, one could say that $g$ is a function from the set $\{x \in \mathbb{R} \mid x \neq 0\}$ of nonzero real numbers, to $\mathbb{R}$.

Intuitively, a function from $A$ to $B$ can be thought of being any process that accepts inputs from the set $A$, and assigns an element of the set $B$ to each of these inputs. The process need not be given by a formula. Indeed, most of the functions that arise in science or in everyday life are not given by any formula.

Example $6.2.4$.

Each point on the surface of the earth has a particular temperature right now, and the temperature (in degrees centigrade) is a real number. Thus, temperature defines a function $\text {temp}$ from the surface of the earth to $\mathbb{R}$: $\text {temp} (x)$ is the temperature at the point $x$.
The items in a grocery store each have a particular price, which is a certain number of cents, so $\text {price}$ can be thought of as a function from the set of items for sale to the set $\mathbb{N}$ of all natural numbers: $\text {price}(x)$ is the price of item $x$ (in cents).
If we let $\text {People}$ be the set of all people (alive or dead), then $\text {mother}$ is a function from $\text {People}$ to $\text {People}$. For example, \[\text { mother(Prince Charles) }=\text { Queen Elizabeth. }\]
(To avoid ambiguity, perhaps we should clarify that, by “mother,” we mean “biological mother.”)
In contrast, $\text {grandmother}$ is not a function from $\text {People}$ to $\text {People}$. This is because people have not just one grandmother, but two (a maternal grandmother and a paternal grandmother). For example, if we say that Prince Charles wrote a poem for his grandmother, we do not know whether he wrote the poem for the mother of Queen Elizabeth, or for his other grandmother. A function is not ever allowed to have such an ambiguity. (In technical terms, $\text {grandmother}$ is a “relation,” not a function. This will be explained in Section $7.1$.)

Functions are often given by a table of values.

Example $6.2.5$.

The list of prices in a store is an example of this:

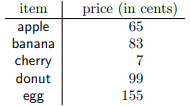
$clipboard_e9f51e8299ed416f348a2bad8ef5f33e0.png$

In this example:

The domain of price is $\text { \{apple, banana, cherry, donut, egg }\}$.
$\text { price(banana) }=83$.
$\text { price(guava) }$ does not exist, because $\text {guava}$ is not in the domain of the function.

Instead of making a table, mathematicians prefer to represent each row of the table by an ordered pair. For example, the first row of the table is $\text {apple } \mid 65$. This has $\text {apple}$ on the left and 65 on the right, so we represent it by the ordered pair $(\text {apple}, 65)$, which has $\text {apple}$ on the left and 65 on the right. The second row is represented by $(\text {banana}, 83)$. Continuing in this way yields a total of 5 ordered pairs (one for each row). To keep them gathered together, a mathematician puts them into a set. Thus, instead of writing a table, a mathematician would represent this function as: \[\{(\text { apple, } 65),(\text { banana }, 83),(\text { cherry, } 7),(\text { donut, } 99),(\text { egg, } 155)\} .\]
The set of ordered pairs contains exactly the same information as a table of values, but the set is a more convenient form for mathematical manipulations.

Exercise $6.2.6$.

At right is a function $f$ given by a table of values. (You do not need to show your work on any parts of this problem.)

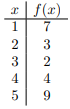
$clipboard_edb7018d1cfac1a658d85b9b89355af80.png$

What is the domain of $f$?
What is $f(3)$?
Represent $f$ as a set of ordered pairs.
Find a formula to represent $f$.
[Hint: There is a formula of the form $f(x) = ax^{2} + bx + c$.]

Example $6.2.7$.

Not every table of values represents a function. For example, suppose we have the following price list, which is a slight change from Example $6.2.5$:

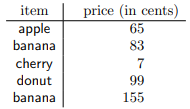
$clipboard_e6fd11f61098e79dc999953a5a242276a.png$

There is a problem here, because there are two possible prices for a banana, depending on which line of the table is looked at. (So you might pick up a banana, expecting to pay 83 cents, and end up having the cashier charge you $1.55.) This is not allowed in a function: each input must have exactly one output, not a number of different possible outputs. Thus, if a table represents a function, and an item appears in the left side of more than one row, then all of those rows must have the same output listed on the right side.

Remark $6.2.8$.

A 2-column table represents a function from $A$ to $B$ if and only if:

every value that appears in the left column of the table is an element of $A$,
every value that appears in the right column of the table is an element of $B$,
every element of $A$ appears in the left side of the table, and
no two rows of the table have the same left side, but different right sides.

Example $6.2.9$.

Which of the following are functions from $\{1, 2, 3\}$ to $\{\text {w, h, o}\}$? (If it is not such a function, then explain why not.)

$\{(1, \mathrm{w}),(1, \mathrm{~h}),(1, \mathrm{o})\}$
$\{(1, \mathrm{~h}),(2, \mathrm{~h}),(3, \mathrm{~h})\}$
$\{(1, \mathrm{~h}),(2, \mathrm{o}),(3, \mathrm{w})\}$
$\{(\mathrm{w}, 1),(\mathrm{h}, 2),(\mathrm{o},3)\}$

Solution

This is not a function. Since $(1, \mathrm{w})$, $(1, \mathrm{~h})$, and $(1,\mathrm{o})$ are all in the set, there are three different elements $b$ (not a unique $b$), such that $(1, b)$ is in the set.
This is such a function.
This is such a function.
This is not such a function, because, for the element $(\mathrm{w}, 1)$ of the set, there do not exist elements $a$ of $\{1, 2, 3\}$ and $b$ of $\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}$, such that $(\mathrm{w}, 1)=(a, b)$. (Instead, we would need to take $a$ in $\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}$ and $b$ in $\{1, 2, 3\}$, which is backwards from what is required. In fact, $f$ is a function from $\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}$ to $\{1, 2, 3\}$, not from $\{1, 2, 3\}$ to $\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}$.)

Exercise $6.2.10$.

Let

$A=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{e}\}$, and
$B=\{1,3,5,7,9,11\}$.

Which of the following sets of ordered pairs are functions from $A$ to $B$? (For those that are not, explain why.)

$\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 7),(\mathrm{e}, 9)\}$
$\{(\mathrm{a}, 1),(\mathrm{b}, 2),(\mathrm{c}, 3),(\mathrm{d}, 4),(\mathrm{e}, 5)\}$
$\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 3),(\mathrm{e}, 1)\}$
$\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 7),(\mathrm{e}, 9),(\mathrm{a}, 11)\}$
$\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{e}, 7)\}$
$\{(\mathrm{a}, 1),(\mathrm{b}, 1),(\mathrm{c}, 1),(\mathrm{d}, 1),(\mathrm{e}, 1)\}$
$\{(\mathrm{a}, \mathrm{a}),(\mathrm{b}, \mathrm{a}),(\mathrm{c}, \mathrm{a}),(\mathrm{d}, \mathrm{a}),(\mathrm{e}, \mathrm{a})\}$
$\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 5),(\mathrm{e}, 3),(\mathrm{a}, 1)\}$
$\{(1, \mathrm{a}),(3, \mathrm{a}),(5, \mathrm{a}),(7, \mathrm{a}),(9, \mathrm{a}),(11, \mathrm{a})\}$
$\{(\mathrm{c}, 1),(\mathrm{b}, 3),(\mathrm{e}, 5),(\mathrm{a}, 7),(\mathrm{d}, 9)\}$

Remark $6.2.11$.

It is sometimes helpful to represent a function $f: A \rightarrow B$ by drawing an arrow diagram:

a dot is drawn for each element of $A$ and each element of $B$, and
an arrow is drawn from $a$ to $f(a)$, for each $a \in A$.

For example, suppose

$A=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{e}\}$,
$B=\{1,2,3,4\}$, and
$f=\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 4),(\mathrm{d}, 4),(\mathrm{e}, 3)\}$.

Then the picture at right is an arrow diagram of $f$.

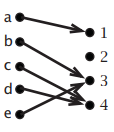
$clipboard_e4291ddfcac4c9fb86b6a84e86dbe9ada.png$

Notice that:

There is exactly one arrow coming out of each element of $A$. This is true for the arrow diagram of any function.
There can be any number of arrows coming into each element of $B$ (perhaps none, perhaps one, or perhaps more than one).

Example \(6.2.1\).

Definition \(6.2.2\) (unofficial).

Example \(6.2.3\).

Example \(6.2.4\).

Example \(6.2.5\).

Exercise \(6.2.6\).

Example \(6.2.7\).

Remark \(6.2.8\).

Example \(6.2.9\).

Exercise \(6.2.10\).

Remark \(6.2.11\).