6.4: One-to-one functions

We begin this section with an example.

Example \(6.4.1\).

1. Suppose Inspector Thinkright knows two facts:
   1. Alice is the thief’s wife, and
   2. Alice is Bob’s wife.
      Then the Inspector can arrest Bob for theft, because a woman cannot be the wife of more than one man.
2. On the other hand, suppose the Inspector knows:
   1. Alice is the forger’s mother, and
   2. Alice is Charlie’s mother.
      Then the Inspector does not know enough to be sure who the forger is, because it could be some other child of Alice, instead of being Charlie.

This example illustrates a fundamental difference between the \(\text{wife}\) function and the \(\text{mother}\) function: two different people can have the same mother, but only one person can have any particular person as their wife. (For example, if Bud and Charlie have the same wife, then “Bud” must be a nickname for Charlie.) In mathematical terms, this important property of the wife function is expressed by saying that the \(\text{wife}\) function is “one-to-one.”

The notion is formalized in the following definition:

Definition \(6.4.2\).

Suppose \(f: A \rightarrow B\). We say \(f\) is one-to-one iff, for all \(a_{1}, a_{2} \in A\), such that \(f(a_{1}) = f(a_{2})\), we have \(a_{1} = a_{2}\).

Exercise \(6.4.3\).

Assume \(f: A \rightarrow B\) and \(g: X \rightarrow Y\). Translate each assertion into FirstOrder Logic. 1) f is one-to-one. 2) g is one-to-one. 3) f is not one-to-one. 4) g is not one-to-one. (Simplify your answers in (3) and (4) so that ¬ is applied only to predicates.)

Remark \(6.4.4\).

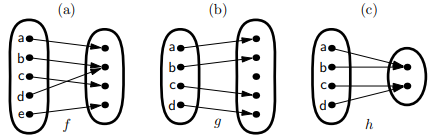
If you have an arrow diagram of a function, then it is easy to tell whether or not the function is one-to-one. For example:

1. The function \(f\) of Figure \(6A(a)\) is not one-to-one. This is because the arrow from \(b\) and the arrow from \(d\) go to the same place, so \(f(b) = f(d)\). In general, if arrows from two different elements of the domain go to the same element of the range, then the function is not one-to-one.
2. The function \(g\) of Figure \(6A(b)\) is one-to-one. This is because the arrows from two different elements of the domain never go to the same element of the range. In short, there is only one element of the domain that goes to any one element of the range. (This is the reason for the terminology “one-to-one.” A function is “two-to-one” if there are two elements of the domain mapping to each element of the range, as is true of the function \(h\) in Figure \(6A(c)\), but we do not need this terminology.)
3. Warning. Although the arrow diagram of a one-to-one function never has more than one arrow pointing to the same element of the codomain, this does not mean that every element of the codomain has exactly one arrow into it. For example, the function \(g\) of Figure \(6A(b)\) is one-to-one (because there is never more than one arrow into any point), but there is a point in the codomain that does not have any arrows to it.

Figure \(6A\). Arrow diagrams of three functions \(f\), \(g\), and \(h\).

Example \(6.4.5\).

Without giving official proofs, let us determine which of the following functions are one-to-one.

1. \(f: \mathbb{R} \rightarrow \mathbb{R}\), defined by \(f(x) = x + 1\).
   This is one-to-one. For any real numbers \(x\) and \(y\), \(f(x) = f(y)\) means that \(x + 1 = y + 1\). Subtracting 1 from both sides of the equation, we conclude that \(x = y\) whenever \(f(x) = f(y)\).
2. \(g: \mathbb{R} \rightarrow \mathbb{R}\), defined by \(g(x) = |x|\). This is not one-to-one. We demonstrate this by finding two distinct real numbers whose image is the same: \[g(1)=|1|=1=|-1|=g(-1) ,\]
   but \(1 \neq-1\). This shows that \(g\) is not one-to-one.
3. \(f:\{1,2,3\} \rightarrow\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}\) defined by \(f=\{(1, b),(2, a),(3, a)\}\).
   This is not one-to-one. We demonstrate this by finding two distinct values in \(\{1,2,3\}\) whose image is the same: f(2) = a = f(3), but 2 ̸= 3. This shows that f is not one-to-one. 4) h: N → N, defined by h(x) = |x|. This is one-to-one. Since all natural numbers are nonnegative, we have |x| = x for every natural number x. So if h(x) = h(y), then x = |x| = h(x) = h(y) = |y| = y.

Remark \(6.4.6\).

These examples demonstrate the general pattern of how to prove a function is (or is not) one-to-one:

• To prove that a function \(f: A \rightarrow B\) is one-to-one, we need to demonstrate that for every \(a_{1}, a_{2} \in A\), if \(f(a_{1}) = f(a_{2})\), then \(a_{1} = a_{2}\).
• To prove that a function \(f: A \rightarrow B\) is not one-to-one, we need only find a single pair of values \(a_{1}, a_{2} \in A\), for which \(f(a_{1}) = f(a_{2})\), but \(a_{1} \neq a_{2}\).

Exercise \(6.4.7\).

Explain why your answers are correct (but you do not need to give formal proofs).

1. Each formula defines a function from \(\mathbb{R}\) to \(\mathbb{R}\). Which of the functions are one-to-one?
   1. \(f(x) = 1\).
   2. \(g(x) = x\).
   3. \(h(x) = x^{2}\).
   4. \(i(x) = 3x + 2\).
   5. \(j(x) = 1/ ( |x| + 1)\).
2. Each of the following sets of ordered pairs is a function from \(\{1,2,3,4\}\) to \(\{a, b, c, d, e\}\). Which are one-to-one?
   1. \(f = \{(1, a),(2, b),(3, d),(4, e)\}\)
   2. \(g = \{(1, c),(2, d),(3, d),(4, e)\}\)
   3. \(h = \{(1, e),(2, d),(3, c),(4, b)\}\)
   4. \(i = \{(1, e),(2, e),(3, e),(4, e)\}\)
   5. \(j = \{(1, a),(2, c),(3, e),(4, c)\}\)
   6. \(k = \{(1, a),(2, c),(3, e),(4, d)\}\)

Here is an example of a formal proof that a function is one-to-one.

Example \(6.4.8\).

Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be defined by \(f(x) = 2x + 1\). Then \(f\) is one-to-one.

Scratchwork. By definition, we wish to show \(\forall x_{1}, x_{2} \in \mathbb{R},\left(f\left(x_{1}\right)=f\left(x_{2}\right) \Rightarrow x_{1}=x_{2}\right)\). Thus, the proof will use \(\forall\)-introduction: the first words in the proof will be “Given \(x_{1}, x_{2} \in \mathbb{R}\)” (or other words to that effect). Then, because we wish to show \(f(x_{1}) = f(x_{2}) \Rightarrow x_{1} = x_{2}\), we will assume \(f(x_{1}) = f(x_{2})\), and the proof will be complete as soon as we can prove \(x_{1} = x_{2}\).

By the definition of \(f\), the assumption \(f(x_{1}) = f(x_{2})\) means that \[2 x_{1}+1=2 x_{2}+1 .\]
Subtracting 1 from both sides, we see that \[2 x_{1}=2 x_{2}.\]
Dividing both sides by 2, we conclude that \(x_{1} = x_{2}\), as desired.

Since readers of this textbook are expected to have a good command of logic and high-school algebra, our official proof can omit the comments that are unnecessary for such a well-educated reader. For example, the reader can be expected to be able to easily verify that the equation \(2x + 1 = 2x2 + 1\) can be simplified to the equation \(2x_{1} = 2x_{2}\), without being told that they should subtract 1 from both sides.

Solution

Given \(x_{1}, x_{2} \in \mathbb{R}\), such that \(f(x_{1}) = f(x_{2})\), we have \[2 x_{1}+1=2 x_{2}+1 ,\]
so \[2 x_{1}=2 x_{2} ,\]
so \(x_{1} = x_{2}\).

A very similar argument applies to other linear functions.

Example \(6.4.9\).

Define \(p: \mathbb{R} \rightarrow \mathbb{R}\) by \(p(z) = 6z − 100\). Show that \(p\) is one-to-one.

Solution

PROOF.

Given \(z_{1}, z_{2} \in \mathbb{R}\), such that \(p(z_{1}) = p(z_{2})\), we have \[6 z_{1}-100=6 z_{2}-100\]
so \[6 z_{1}=6 z_{2} ,\]
so \(z_{1} = z_{2}\).

Exercise \(6.4.10\).

Prove that each function is one-to-one.

1. \(f: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x) = 3x + 5\).
2. \(f: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x) = 7x − 2\).
3. \(g: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(g(t) = 4t + 9\).
4. \(h: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(h(s) = 7 − 8s\).
5. \(i: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(i(r) = (5r − 2)/7\).
6. \(j : \mathbb{Z} \rightarrow \mathbb{Z}\) defined by \(j(n) = 2n + 11\).

The fact that the \(\text{wife}\) function is one-to-one can be restated as the fact that two different people cannot have the same wife. In general, a function is one-to-one iff two different elements of the domain always map to two different elements of the range:

A function \(f: A \rightarrow B\) is one-to-one if and only if
\(\forall a_{1}, a_{2} \in A,\left(a_{1} \neq a_{2} \Rightarrow f\left(a_{1}\right) \neq f\left(a_{2}\right)\right).\)

(The notation “\(\forall a_{1}, a_{2} \in A\)” is short for “\(\forall a_{1} \in A, \forall a_{2} \in A\).”)

We should justify the assertion in this box with a proof. The implication \(\Rightarrow\) is proved in the following theorem; the other direction is an exercise.

Theorem \(6.4.12\).

If a function \(f: A \rightarrow B\) is one-to-one, then \[\forall a_{1}, a_{2} \in A,\left(a_{1} \neq a_{2} \Rightarrow f\left(a_{1}\right) \neq f\left(a_{2}\right)\right).\]

Proof

Let \(f: A \rightarrow B\) be one-to-one. Given \(a_{1}, a_{2} \in A\), we know, from the definition of one-to-one, that \[f\left(a_{1}\right)=f\left(a_{2}\right) \Rightarrow a_{1}=a_{2} .\]

So the contrapositive of this implication is also true. That is, a1 ̸= a2 ⇒ f(a1) ̸= f(a2).

Exercise \(6.4.13\).

1. Prove the converse of Theorem \(6.4.12\). More precisely, assume \(f: A \rightarrow B\), and show that if \[\forall a_{1}, a_{2} \in A,\left(a_{1} \neq a_{2} \Rightarrow f\left(a_{1}\right) \neq f\left(a_{2}\right)\right) ,\]
   then f is one-to-one.
2. Assume:
   1. \(f: A \rightarrow B\),
   2. \(f\) is one-to-one,
   3. \(a_{1}, a_{2} \in A\),
   4. \(g: B \rightarrow C\),
   5. \(g\) is one-to-one,
   6. \(b_{1}, b_{2} \in B\),
   7. \(f(a_{1}) = b_{1}\),
   8. \(f(a_{2}) = b_{2}\), and
   9. \(g(b_{1}) = g(b_{2})\).

Show \(a_{1} = a_{2}\). [Hint: First use the fact that \(g\) is one-to-one, then the fact that \(f\) is one-to-one.]

Remark \(6.4.14\).

(alternative terminology). Many mathematicians use the word “injective,” rather than “one-to-one.” (This comes from French.) Also, a function that is one-to-one can be called an injection.