8.1: The Principle of Mathematical Induction

Reminder \(8.1.1\).

To say that \(P(n)\) is a predicate of natural numbers, means that, for each natural number \(n\), we have an assertion \(P(n)\) that is either true or false. Some examples of predicates are:

• Let \(P_{odd}(n)\) be the assertion “\(n\) is odd.”
• Let \(P_{big}(n)\) be the assertion “\(n > 1000\).”
• Let \(P_{square}(n)\) be the assertion “\(\exists k \in \mathbb{N},\left(n=k^{2}\right)\).”
• Let \(P_{prime}(n)\) be the assertion “\(n\) is a prime number.”

Mathematicians accept the truth of the following assertion as a basic fact about the natural numbers:

Axiom \(8.1.2\). (Principle of Mathematical Induction).

Suppose \(P(n)\) is a predicate of natural numbers. If

1. \(P(1)\) is true, and
2. for every \(k \geq 2\), (\(P(k-1) \Rightarrow P(k)\)) ,
   then \(P(n)\) is true for all \(n \in \mathbb{N}^{+}\).

Although we cannot prove Axiom \(8.1.2\), it can be given an informal justification that may convince you to accept it as a valid property of \(\mathbb{N}\):

Proof

INFORMAL JUSTIFICATION.

Let \(n\) be an arbitrary element of \(\mathbb{N}^{+}\).

• From (i), we know \(P(1)\) is true.
• From (ii), we know \(P(2-1) \Rightarrow P(2)\) is true.
  Since \(P(2-1)=P(1)\) is true, we conclude, by \(\Rightarrow\)-elimination, that \(P(2)\) is true.
• From (ii), we know \(P(3-1) \Rightarrow P(3)\) is true.
  Since \(P(3 − 1) = P(2)\) is true, we conclude, by \(\Rightarrow\)-elimination, that \(P(3)\) is true.
  .
  .
  .
• From (ii), we know \(P(n − 1) \Rightarrow P(n)\) is true.
  Since \(P(n − 1)\) is true, we conclude, by \(\Rightarrow\)-elimination, that \(P(n)\) is true. Since \(n\) is an arbitrary element of \(\mathbb{N}^{+}\), we conclude that \(P(n)\) is true for all \(n \in \mathbb{N}^{+}\).

Terminology \(8.1.3\).

• In a proof using Mathematical Induction, establishing (i) is called the base case, and establishing (ii) is the induction step.
• In the induction step, we are proving \(P(k − 1) \Rightarrow P(k)\), so we assume that \(P(k − 1)\) is true (and establish \(P(k)\)). This assumption \(P(k−1)\) is called the induction hypothesis.

Here is an example of how mathematical induction can be used.

Proposition \(8.1.4\).

For every \(n \in \mathbb{N}^{+}\), we have \(1+2+3+\cdots+n=\frac{n(n+1)}{2}\).

Proof

PROOF BY INDUCTION.

Define \(P(n)\) to be the assertion \[1+2+3+\cdots+n=\frac{n(n+1)}{2} .\]

1. Base case. For \(n = 1\), we have \[1+2+3+\cdots+n=1 \quad \text { and } \quad \frac{n(n+1)}{2}=\frac{1(1+1)}{2}=1 .\]
   Since these are equal, \(P(1)\) is true.
2. Induction step. Assume \(P(k − 1)\) is true (and \(k \geq 2\)). This means that \[1+2+3+\cdots+(k-1)=\frac{(k-1)((k-1)+1)}{2} .\]
   Hence \[\begin{aligned}
   1+2 &+3+\cdots+k \\
   &=(1+2+3+\cdots+(k-1))+k \\
   &=\frac{(k-1)((k-1)+1)}{2}+k \\
   &=\frac{(k-1) k}{2}+k \\
   &=k\left(\frac{k-1}{2}+1\right) \\
   &=k\left(\frac{k+1}{2}\right) \\
   &=\frac{k(k+1)}{2},
   \end{aligned}\]
   (Third Line: Induction Hypothesis)
   so \(P(k)\) is true.

Therefore, by the Principle of Mathematical Induction, we know \(P(n)\) is true for all \(n\). This means \[1+2+3+\cdots+n=\frac{n(n+1)}{2}\]
for every \(n \in \mathbb{N}^{+}\).

Remark \(8.1.5\).

A proof by induction is often used to show that two functions \(f(n)\) and \(g(n)\) are equal. (Proposition \(8.1.4\) is an example of this, with \(f(n)=1+2+3+\cdots+n\) and \(g(n)=n(n+1) / 2\).) The base case is usually easy: calculate \(f(1)\) and \(g(1)\), then notice that they are equal. On the other hand, it is usually not immediately obvious how to do the induction step, so it is a good idea to start by doing some scratch work:

• Write down the desired equality \(f(k) \stackrel{?}{=} g(k)\).
• Then use algebraic simplifications to arrive at a true statement. At some point in these manipulations, you will use the induction hypothesis to replace \(f(k − 1)\) with \(g(k − 1)\), or vice-versa.

A proof can then be obtained by rewriting these algebraic steps in a logical order (preferably, as a “one-line proof” — a string of equalities that starts with \(f(k)\) and ends with \(g(k)\)).

For example, the scratch work that led to the above proof of Proposition \(8.1.4\) can be found in Figure \(8A\) below. In this case, the algebraic manipulations are fairly simple, but some problems are considerably more difficult.

Figure \(8A.\) Scratch work for the proof of Proposition \(8.1.4\).

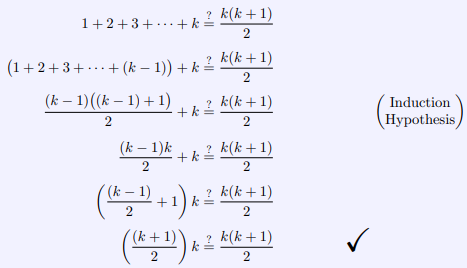
Here is another example that is fairly straightforward:

Proposition \(8.1.6\).

For every \(n \in \mathbb{N}^{+}\), we have \[3+7+11+\cdots+(4 n-1)=2 n^{2}+n\]

Proof

PROOF BY INDUCTION.

Define \(P(n)\) to be the assertion \[3+7+11+\cdots+(4 n-1)=2 n^{2}+n .\]

1. Base case. For \(n = 1\), we have \[3+7+11+\cdots+(4 n-1)=3 \quad \text { and } \quad 2 n^{2}+n=2\left(1^{2}\right)+1=3 .\]
   Since these are equal, \(P(1)\) is true.
2. Induction step. Assume \(P(k − 1)\) is true (and \(k \geq 2\)). This means that \[3+7+11+\cdots+(4(k-1)-1)=2(k-1)^{2}+(k-1) .\]
   Hence \[\begin{aligned}
   3+7 &+11+\cdots+(4 k-1) \\
   &=(3+7+11+\cdots+(4(k-1)-1))+(4 k-1) \\
   &=\left(2(k-1)^{2}+(k-1)\right)+(4 k-1) \\
   &=\left(2\left(k^{2}-2 k+1\right)+(k-1)\right)+(4 k-1) \\
   &=\left(2 k^{2}-4 k+2\right)+(k-1)+(4 k-1) \\
   &=2 k^{2}+k ,
   \end{aligned}\]
   (Third Line: Induction Hypothesis)
   so \(P(k)\) is true.

Therefore, by the Principle of Mathematical Induction, we know \(P(n)\) is true for all \(n\). This means \[3+7+11+\cdots+(4 n-1)=2 n^{2}+n
for every \(n \in \mathbb{N}^{+}\).

Exercise \(8.1.7\).

Prove each formula by Mathematical Induction.

1. \(2+4+6+8+\cdots+2 n=n(n+1).\)
2. \(1+3+5+7+\cdots+(2 n-1)=n^{2} .\)
3. \(2+7+12+17+\cdots+(5 n-3)=\frac{n(5 n-1)}{2} .\)

Notation \(8.1.8\).

It is often necessary to add up a long list of numbers (as in the above exercises), so it is convenient to have a good notation for this: if \(a_{1}, a_{2}, \ldots, a_{n}\) is any sequence of numbers, then the sum \(a_{1}+a_{2}+\cdots+a_{n}\) can be denoted by \[\sum_{k=1}^{n} a_{k} .\]
(The symbol \(\sum\) is a capital sigma, the Greek version of the letter \(S\) — it stands for “sum.”)

Example \(8.1.9\).

Let \(a_{1}, a_{2}, \ldots, a_{n}\) be a sequence of numbers. Then:

1. \(\sum_{k=1}^{1} a_{k}=a_{1}, \quad \sum_{k=1}^{2} a_{k}=a_{1}+a_{2}, \quad \text { and } \quad \sum_{k=1}^{3} a_{k}=a_{1}+a_{2}+a_{3} .\)
2. \(\sum_{k=1}^{1} k=1, \quad \sum_{k=1}^{2} k=1+2=3, \quad \sum_{k=1}^{3} k=1+2+3=6.\)
3. \(\sum_{k=1}^{n} k=1+2+3+\cdots+n.\)
4. For any \(n \in \mathbb{N}^{+}\), we have \(\sum_{k=1}^{n} a_{k}=\left(\sum_{k=1}^{n-1} a_{k}\right)+a_{n}.\)

Exercise \(8.1.10\).

1. In Exercise \(8.1.7\), the left-hand side of each formula is a sum. Write each of these sums in \(\sum\)-notation.
2. Show that (1) and (4) of Example \(8.1.9\) imply \(\sum_{k=1}^{0} a_{k}=0 .\)

Remark \(8.1.11\).

In the Induction Step of a proof by induction, we wish to prove \[\forall k \geq 2,(P(k-1) \Rightarrow P(k)) .\]
Since \(k\) is a bound (“dummy”) variable in this assertion, there is no harm in replacing it with a different letter: for example, if you prefer, it is perfectly acceptable to prove, say, \[\forall i \geq 2,(P(i-1) \Rightarrow P(i)), \quad \text { or } \quad \forall n \geq 2,(P(n-1) \Rightarrow P(n)) .\]
This is important to keep in mind when the variable \(k\) is already being used for something else.

Example \(8.1.12\).

Show that \(\sum_{k=1}^{n}(2 k-5)=n^{2}-4 n .\)

Solution

PROOF BY INDUCTION.

Define \(P(n)\) to be the assertion \[\sum_{k=1}^{n}(2 k-5)=n^{2}-4 n.\]

1. Base case. For \(n = 1\), we have \[\sum_{k=1}^{n}(2 k-5)=\sum_{k=1}^{1}(2 k-5)=2(1)-5=-3=1^{2}-4(1)=n^{2}-4 n.\]
   So P(1) is true.
2. Induction step. Assume \(n \geq 2\) and \(P(n − 1)\) is true. This means that \[\sum_{k=1}^{n-1}(2 k-5)=(n-1)^{2}-4(n-1).\]
   Hence \[\begin{aligned}
   \sum_{k=1}^{n}(2 k-5) &=\left(\sum_{k=1}^{n-1}(2 k-5)\right)+(2 n-5) \\
   &=\left((n-1)^{2}-4(n-1)\right)+(2 n-5) \\
   &=\left(\left(n^{2}-2 n+1\right)-4 n+4\right)+(2 n-5) \\
   &=n^{2}-4 n,
   \end{aligned}\]
   (Second Line: Induction Hypothesis)
   so \(P(n)\) is true.

Therefore, by the Principle of Mathematical Induction, we conclude that \(P(n)\) is true for every \(n \in \mathbb{N}^{+}\).

Exercise \(8.1.13\).

Prove each formula by induction.

1. \(\sum_{k=1}^{n}(6 k+7)=3 n^{2}+10 n.\)
2. \(\sum_{k=1}^{n}(4 k-5)=2 n^{2}-3 n.\)
3. \(\sum_{k=1}^{n}(12 k-19)=6 n^{2}-13 n .\)
4. \(\sum_{k=1}^{n}(3 k+11)=\frac{3 n^{2}+25 n}{2}.\)
5. \(\sum_{k=1}^{n} 3^{k}=\frac{3^{n+1}-3}{2} .\)
6. \(\sum_{k=1}^{n} 3^{k}=\frac{3^{n+1}-3}{2}.\)
7. \(\sum_{k=1}^{n} k^{2}=\frac{n(n+1)(2 n+1)}{6}.\)
8. \(\text { (harder) } \sum_{k=1}^{n} k^{3}=\left(\frac{n(n+1)}{2}\right)^{2} .\)

Remark \(8.1.14\).

If you wish to prove that \(P(k)\) is true for all \(k\), then the Principle of Induction can be applied with \(k\) in the role of \(n\). This is called “inducting on \(k\).” Similarly, any other letter can be used in place of \(n\).

Example \(8.1.15\).

Show, for all \(k \in \mathbb{N}^{+}\), that \[\sum_{i=1}^{k}\left(3 i^{2}-3 i+1\right)=k^{3} .\]

Solution

PROOF BY INDUCTION.

Define \(P(k)\) to be the assertion \[\sum_{i=1}^{k}\left(3 i^{2}-3 i+1\right)=k^{3} .\]

1. Base case. For \(k = 1\), we have \[\sum_{i=1}^{k}\left(3 i^{2}-3 i+1\right)=\sum_{i=1}^{1}\left(3 i^{2}-3 i+1\right)=3(1)^{2}-3(1)+1=1=1^{3}=k^{3} .\]
   So \(P(1)\) is true.
2. Induction step. Assume \(k \geq 2\) and \(P(k − 1)\) is true. This means that \[\sum_{i=1}^{k-1}\left(3 i^{2}-3 i+1\right)=(k-1)^{3} .\]
   Hence \[\begin{aligned}
   \sum_{i=1}^{k}\left(3 i^{2}-3 i+1\right) &=\left(\sum_{i=1}^{k-1}\left(3 i^{2}-3 i+1\right)\right)+\left(3 k^{2}-3 k+1\right) \\
   &=(k-1)^{3}+\left(3 k^{2}-3 k+1\right) \\
   &=\left(k^{3}-3 k^{2}+3 k-1\right)+\left(3 k^{2}-3 k+1\right) \\
   &=k^{3},
   \end{aligned}\]
   (Second Line: Induction Hypothesis)
   so \(P(k)\) is true.

By the Principle of Mathematical Induction, we conclude that \(P(k)\) is true for all \(k \in \mathbb{N}^{+}\).