8.2: Other Proofs by Induction
- Page ID
- 23928
Not all proofs by induction are about sums:
Suppose \(a, b, n \in \mathbb{Z}\), with \(a \equiv b(\bmod n)\). Show \(a^{k} \equiv b^{k}(\bmod n)\), for all \(k \in \mathbb{N}^{+}\).
Solution
We induct on \(k\). Define \(P(k)\) to be the assertion \[a^{k} \equiv b^{k}(\bmod n) .\]
- Base case. Since \(a^{1} = a\) and \(b^{1} = b\), the hypothesis \(a \equiv b(\bmod n)\) tells us that \[a^{1} \equiv b^{1}(\bmod n) ,\]
so P(1) is true. - Induction step. Assume \(P(k − 1)\) is true. This means that \[a^{k-1} \equiv b^{k-1}(\bmod n) .\]
By assumption, we also have \[a \equiv b(\bmod n) .\]
Exercise \(5.1.19(3)\) tells us that the product of congruent quantities is congruent, so we can multiply the above congruences, to conclude that \[\left(a^{k-1}\right)(a) \equiv\left(b^{k-1}\right)(b)(\bmod n) .\]
In other words, \[a^{k} \equiv b^{k}(\bmod n) ,\]
so \(P(k)\) is true.
Therefore, by the Principle of Mathematical Induction, \(P(k)\) is true for every \(k \in \mathbb{N}^{+}\).
Prove each of the following assertions by induction.
- \(5^{k} \equiv 5(\bmod 4)\), for every \(k \in \mathbb{N}^{+}\).
- \(n^{3} \equiv n(\bmod 3)\) for every \(n \in \mathbb{N}^{+}\).
The Principle of Mathematical Induction is an important tool for proving things about sequences of numbers in which each term is defined from preceding terms. (Such sequences are said to be defined “recursively” or “inductively.”) Fibonacci numbers are one famous example of this. In this case, each term is the sum of the two preceding terms:
The Fibonacci numbers \(F_{1}, F_{2}, F_{3}, \ldots\) are defined by:
- \(F_{1} = 1\),
- \(F_{2} = 1\), and
- \(F_{n} = F_{n−1} + F_{n−2}\) for \(n \geq 3\).
(For example, \(F_{3}=F_{3-1}+F_{3-2}=F_{2}+F_{1}=1+1=2\).) In general, each Fibonacci number (after \(F_{2}\)) is the sum of the two preceding Fibonacci numbers, so the first few Fibonacci numbers are: \[\begin{array}{c||c|c|c|c|c|c|c|c}
n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \cdots \\
\hline F_{n} & 1 & 1 & 2 & 3 & 5 & 8 & 13 & \cdots
\end{array}\]
Prove \(\sum_{k=1}^{n} F_{k}=F_{n+2}-1\) for all \(n \in \mathbb{N}^{+}\).
Solution
Define \(P(n)\) to be the assertion \[\sum_{k=1}^{n} F_{k}=F_{n+2}-1 .\]
- Base case. For \(n = 1\), we have \[\sum_{k=1}^{n} F_{k}=\sum_{k=1}^{1} F_{k}=F_{1}=1=2-1=F_{3}-1=F_{1+2}-1=F_{n+2}-1 ,\]
so \(P(1)\) is true. - Induction step. Assume \(P(n − 1)\) is true (and \(n \geq 2\)). Then \[\begin{aligned}
\sum_{k=1}^{n} F_{k} &=\left(\sum_{k=1}^{n-1} F_{k}\right)+F_{n} \\
&=\left(F_{(n-1)+2}-1\right)+F_{n} \\
&=\left(F_{n+1}-1\right)+F_{n} \\
&=\left(F_{n+1}+F_{n}\right)-1 \\
&=F_{n+2}-1
\end{aligned}\]
(Second Line: Induction Hypothesis, Last Line: definition of Fibonacci number).
Therefore, by the Principle of Mathematical Induction, \(P(n)\) is true for every \(n\). This means \(\sum_{k=1}^{n} F_{k}=F_{n+2}-1\) for all \(n \in \mathbb{N}^{+}\).
Prove each assertion by induction.
- \(\sum_{k=1}^{n} F_{k}^{2}=F_{n} F_{n+1}\).
- \(F_{3k}\) is even, for all \(k \in \mathbb{N}^{+}\).
- \(F_{4k}\) is divisible by 3, for all \(k \in \mathbb{N}^{+}\).
Induction can also be applied to other sequences that are defined recursively:
Define a sequence \(\left\{a_{n}\right\}\) by:
- \(a_{1} = 1\), and
- \(a_{n} = 2a_{n−1} + 1\) for \(n \geq 2\).
Show \(a_{n} = 2^{n} − 1\) for all \(n \in \mathbb{N}^{+}\).
Solution
Define \(P(n)\) to be the assertion \[a_{n}=2^{n}-1 .\]
- Base case. For \(n = 1\), we have \[a_{n}=a_{1}=1 \quad \text { and } \quad 2^{n}-1=2^{1}-1=2-1=1 .\]
Since these are equal, we know that \(P(1)\) is true. - Induction step. Assume \(P(k − 1)\) is true (and \(k \geq 2\)). This means that \[a_{k-1}=2^{k-1}-1 .\]
Then \[\begin{aligned}
a_{k} &=2 a_{k-1}+1 \\
&=2\left(2^{k-1}-1\right)+1 \\
&=\left(2^{k}-2\right)+1 \\
&=2^{k}-1 ,
\end{aligned}\]
(First Line: definition of \(a_{k}\), Second Line: Induction Hypothesis)
so \(P(k)\) is true.
Therefore, by the Principle of Mathematical Induction, \(P(n)\) is true for every \(n\). This means \(a_{n} = 2^{n} − 1\) for all \(n \in \mathbb{N}^{+}\).
The Italian mathematician Fibonacci discovered the Fibonacci numbers in 1202, as the answer to a problem about the population growth of rabbits. Namely, assume that:
- You start with 1 pair of newborn rabbits (a male and a female).
- Each female gives birth to another pair of rabbits each month (a male and a female), starting when she is two months old. (And rabbits never die.)
This means that the pairs of rabbits you have in the nth month consist of the pairs you already had last month, plus one new pair for each pair that you had two months ago. Therefore, if \(F_{n}\) is the number of pairs in the nth month, then \(F_{n}=F_{n-1}+F_{n-2}\). You can read more about Fibonacci numbers on Wikipedia.
- Define a sequence \(\left\{b_{n}\right\}\) by:
- \(b_{1} = 4\), and
- \(b_{n} = 3b_{n−1} − 2 for \(n \geq 2\).
Show \(b_{n} = 3^{n} + 1\) for all \(n \in \mathbb{N}^{+}\).
- Define a sequence \(\left\{c_{n}\right\}\) by:
- \(c_{1} = 25\), and
- \(c_{n} = 4c_{n−1} + 5^{n}\) for \(n \geq 2\).
Show \(c_{n} = 5^{n+1}\) for all \(n \in \mathbb{N}^{+}\).
- Define a sequence \(\left\{d_{n}\right\}\) by:
- \(d_{1} = 3\), and
- \(d_{n} = 2d_{n−1} − n + 2\) for \(n \geq 2\).
Show \(d_{n} = 2^{n} + n\) for all \(n \in \mathbb{N}^{+}\).
- Define a sequence \(\left\{e_{n}\right\}\) by:
- \(e_{1} = 2\), and
- \(e_{n} = 2e_{n−1} − n + 1\) for \(n \geq 2\).
Show \(e_{n} = n + 1\) for all \(n \in \mathbb{N}^{+}\).
Induction is not only for proving that things are equal. For example, it can also be used to prove inequalities:
Prove \(2^{n} \geq n\) for all \(n \in \mathbb{N}^{+}\).
Scratchwork. \[\begin{aligned}
2^{n} & \stackrel{?}{>} n \\
2 \cdot 2^{n-1} & \stackrel{?}{>n} \\
2(n-1) & \geq n \\
n & \geq 2
\end{aligned}\]
(Third Line: Induction Hypothesis, Last Line: \(\sqrt{ }\))
Solution
Define \(P(n)\) to be the assertion \[2^{n}>n\]
- Base case. For \(n = 1\), we have \[2^{n}=2^{1}=2>1=n,\]
so \(P(1)\) is true. - Induction step. Assume \(P(n − 1)\) is true (and \(n \geq 2\)). This means that \[2^{n-1}>n-1 .\]
Then \[\begin{aligned}
2^{n} &=2 \cdot 2^{n-1} \\
&>2(n-1) \\
&=n+(n-2) \\
& \geq n+0 \\
&=n ,
\end{aligned}\]
(Second Line: Induction Hypothesis, Fourth Line: \(n \geq 2\), so \(n - 2 \geq 0\))
so \(P(n)\) is true.
Therefore, by the Principle of Mathematical Induction, \(P(n)\) is true for every natural number \(n\).
- Prove \(3^{n} \geq 3n\) for all \(n \in \mathbb{N}^{+}\). [Hint: Note that \(3^{n} − 3^{n−1} > 3n − 3(n − 1)\) if \(n \geq 2\).]
- Prove \((1 + x)^{n} \geq 1 + nx\) for all \(x \in \mathbb{R}^{+}\) and all \(n \in \mathbb{N}^{+}\).
Here is a standard piece of advice:
Whenever you need to prove a statement with an n in it, you should consider using induction.
(assumes familiarity with polynomials). Prove by induction on \(n\) that the polynomial \(x^{n} − y^{n}\) is divisible by \(x − y\), for all \(n \in N\mathbb{+}\). [Hint: What is \((x − y)x^{n} + y(x^{n} − y^{n})\)?]
(assumes familiarity with commutative groups). Suppose \((G, +)\) is a commutative group. For \(g \in G\) and \(n \in \mathbb{N}^{+}\), we define \(ng\) recursively, by: \[1 g=g \quad \text { and } \quad(n+1) g=n g+g .\]
Prove by induction on \(n\) that \((m + n)g = mg + ng\) for all \(m, n \in \mathbb{N}^{+}\).
Explain what is wrong with the following famous “proof” that all horses have the same colour.
ATTEMPT AT A PROOF BY INDUCTION.
Define \(P(n)\) to be the assertion
“In every set of n horses, all of the horses have the same colour.”
- Base case. For \(n = 1\), let \(H\) be any set of \(n\) horses. Since \(n = 1\), there is only one horse in \(H\), so it is obvious that all of the horses in \(H\) have the same colour.
- Induction step. Assume, for every set of \(n − 1\) horses, that all of the horses have the same colour (and \(n \geq 2\)). Let \(H\) be any set of \(n\) horses.
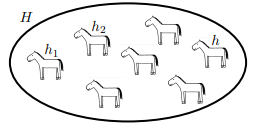
Remove one horse \(h_{1}\) from \(H\) to form a set \(H_{1}\) of \(n − 1\) horses. By the induction hypothesis, we know that
(\(8.2.15\)) all of the horses in \(H_{1}\) have the same colour.
Now, remove some other horse \(h_{2}\) from \(H\) to form a different set \(H_{2}\) of \(n−1\) horses. By applying the induction hypothesis again, we know that
(\(8.2.16\)) all of the horses in H2 have the same colour.
Now, choose \(h\) to be some other horse (neither \(h_{1}\) nor \(h_{2}\)). Since \(h \neq h_{1}\), we know \(h \in H_{1}\), so, from (\(8.2.15\)), we know that all of the horses in \(H_{1}\) have the same colour as \(h\). Similarly, since \(h \neq h_{2}\), we know \(h \in H_{2}\), so, from (\(8.2.16\)), we know that all of the horses in \(H_{2}\) also have the same colour as \(h\). This means all of the horses in \(H_{1} \cup H_{2}\) have the same colour (namely, the colour of horse \(h\)). Since it is clear that \(H = H_{1} \cup H_{2}\) (because \(H_{1}\) contains every horse except \(h_{1}\), which is in \(H_{2}\)), we conclude that all of the horses in \(H\) have the same colour.
By the Principle of Mathematical Induction, we conclude that, in every (finite) set of horses, all of the horses have the same colour.

WARNING. Mathematical induction is a method that is used extensively by mathematicians and computer scientists. However, other scientists (and also philosophers) use the word “induction” to refer to a quite different method of reasoning: scientific induction (or “inductive reasoning”) is the process of deriving a general rule from specific examples. (It is the opposite of deductive reasonin3g, where specific conclusions are derived from general rules.) For example, a scientist might measure the length and the width of very many rectangles, and compare with the areas of the rectangles. He or she would find that the area always came out to be the product of the length with the width. The scientist would then conclude (by inductive reasoning) that the area of every rectangle is the product of its length and its width. However, this does not constitute a mathematical proof of the formula for the area of a rectangle


