2.4E: Infinite Limits EXERCISES

Last updated
Save as PDF

Page ID: 20569

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

2.4: Infinite Limit Exercises

In the following exercises, find the limit.

In the following exercises, consider the graph of the function $y=f(x)$ shown here. Which of the statements about $y=f(x)$ are true and which are false? Explain why a statement is false.

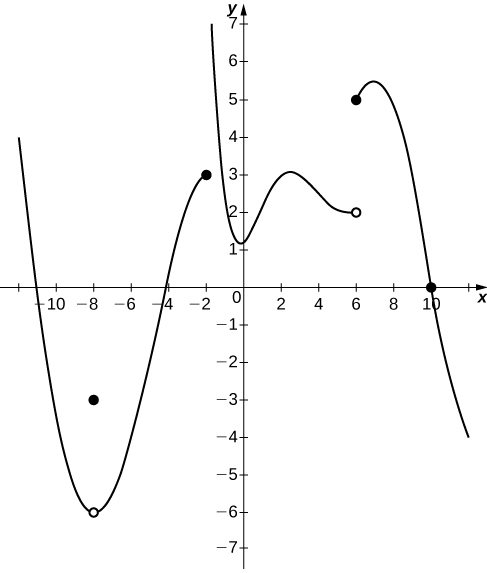
$CNX_Calc_Figure_02_02_201.jpeg$

J46) $\displaystyle \lim_{x→10}f(x)=0$

J47) $\displaystyle \lim_{x→−2^+}f(x)=3$

Answer:: False; $\displaystyle \lim_{x→−2^+}f(x)=+∞$

J48) $\displaystyle \lim_{x→−8}f(x)=f(−8)$

J49) $\displaystyle \lim_{x→6}f(x)=5$

Answer:: False; $\displaystyle \lim_{x→6}f(x)$ DNE since$\displaystyle \lim_{x→6^−}f(x)=2$ and $\displaystyle \lim_{x→6^+}f(x)=5$.

J2.4.1)

a. $\displaystyle \lim_{x→−3^+}\frac{x}{x+3}$

b. $\displaystyle \lim_{x→−3^-}\frac{x}{x+3}$

c. $\displaystyle \lim_{x→−3}\frac{x}{x+3}$

Answer:: a. −∞
b. ∞
c. DNE

J2.4.2) $\displaystyle \lim_{x→0}\ln |x|$

J2.4.3)

a. $\displaystyle \lim_{x→5^+}\frac{2}{x-5}$

b. $\displaystyle \lim_{x→5^-}\frac{2}{x-5}$

c. $\displaystyle \lim_{x→5}\frac{2}{x-5}$

Answer:: a. ∞
b. −∞
c. DNE

J2.4.4)

a. $\displaystyle \lim_{x→-2^+}\frac{x}{(x+2)^2}$

b. $\displaystyle \lim_{x→-2^-}\frac{x}{(x+2)^2}$

c. $\displaystyle \lim_{x→-2}\frac{x}{(x+2)^2}$

J2.4.5)

a. $\displaystyle \lim_{x→6^+}\frac{x}{(6-x)^2}$

b. $\displaystyle \lim_{x→6^-}\frac{x}{(6-x)^2}$

c. $\displaystyle \lim_{x→6}\frac{x}{(6-x)^2}$


Answer:: a. ∞
b. ∞
c. ∞

J2.4.6)

a. $\displaystyle \lim_{x→1^+}\frac{2x^2+7x−4}{x^2+x−2}$

b. $\displaystyle \lim_{x→1^−}\frac{2x^2+7x−4}{x^2+x−2}$

c.$\displaystyle \lim_{x→1}\frac{2x^2+7x−4}{x^2+x−2}$

J2.4.7) $\displaystyle \lim_{x→1}\frac{x^3−1}{x^2−1}$

Answer:: $\displaystyle lim_{x→1}\frac{x^3−1}{x^2−1}=\displaystyle \lim_{x→1}\frac{(x-1)(x^2+x+1)}{(x-1)(x+1)}=\displaystyle \lim_{x→1}\frac{x^2+x+1}{x+1}=\frac{3}{2}$

J2.4.8) $\displaystyle \lim_{x→1/2}\frac{2x}{2x−1}$

J2.4.9) $\displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}$

Answer:: $\displaystyle \lim_{x→ 1/2}\frac{2x^2+3x−2}{2x−1}=\displaystyle \lim_{x→1/2}\frac{(2x−1)(x+2)}{2x−1}=\displaystyle \lim_{x→1/2}(x+2)=\frac{5}{2}$

State the vertical asymptote for each function, if any.

J2.4.10) $f(x)=\ln x$

J2.4.11) $g(x)=\frac{x+5}{x-4}$

Answer:: $x=4$

J2.4.12) $g(x)=\frac{7}{x+5}$

J2.4.13) $g(x)=\frac{7}{x}$

Answer:: $x=0$

J2.4.14)

a. $\displaystyle \lim_{x→\frac{\pi}{2}^+}\tan x=$

b. $\displaystyle \lim_{x→\frac{\pi}{2}^-}\tan x=$

c. $\displaystyle \lim_{x→\frac{\pi}{2}}\tan x=$

d. Does $f(x)=\tan x$ have a vertical asymptote at $x=\frac{\pi}{2}$?