3.6: Derivatives as Rates of Change
- Last updated
- Save as PDF
- Page ID
- 20607
In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. These applications include acceleration and velocity in physics, population growth rates in biology, and marginal functions in economics.
Amount of Change Formula
One application for derivatives is to estimate an unknown value of a function at a point by using a known value of a function at some given point together with its rate of change at the given point. If \(f(x)\) is a function defined on an interval \([a,a+h]\), then the amount of change of \(f(x)\) over the interval is the change in the \(y\) values of the function over that interval and is given by
\[f(a+h)−f(a).\]
The average rate of change of the function \(f\) over that same interval is the ratio of the amount of change over that interval to the corresponding change in the \(x\) values. It is given by
\[\frac{f(a+h)−f(a)}{h}.\]
As we already know, the instantaneous rate of change of \(f(x)\) at \(a\) is its derivative
\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}.\]
For small enough values of \(h\),
\[f′(a)≈\frac{f(a+h)−f(a)}{h}.\]
We can then solve for \(f(a+h)\) to get the amount of change formula:
\[f(a+h)≈f(a)+f′(a)h.\]
We can use this formula if we know only \(f(a)\)and \(f′(a)\) and wish to estimate the value of \(f(a+h)\). For example, we may use the current population of a city and the rate at which it is growing to estimate its population in the near future. As we can see in Figure, we are approximating \(f(a+h)\) by the \(y\) coordinate at a+h on the line tangent to \(f(x)\) at \(x=a\). Observe that the accuracy of this estimate depends on the value of \(h\) as well as the value of \(f′(a)\).
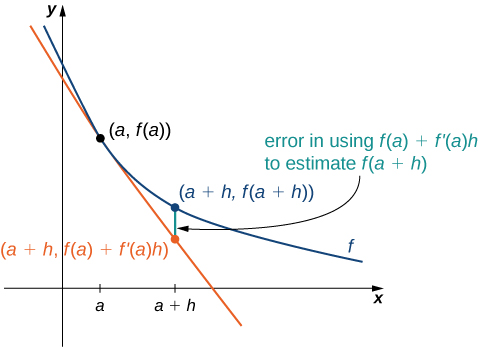
Figure \(\PageIndex{1}\): The new value of a changed quantity equals the original value plus the rate of change times the interval of change: \(f(a+h)≈f(a)+f′(a)h.\)
Example \(\PageIndex{1}\): Estimating the Value of a Function
If \(f(3)=2\) and \(f′(3)=5\), estimate \(f(3.2)\).
Solution
Begin by finding \(h\). We have \(h=3.2−3=0.2.\) Thus,
\(f(3.2)=f(3+0.2)≈f(3)+(0.2)f′(3)=2+0.2(5)=3.\)
Exercise \(\PageIndex{1}\)
Given \(f(10)=−5\) and \(f′(10)=6\), estimate \(f(10.1)\).
- Hint
-
Use the same process as in the preceding example.
- Answer
-
\(−4.4\)
Motion along a Line
Another use for the derivative is to analyze motion along a line. We have described velocity as the rate of change of position. If we take the derivative of the velocity, we can find the acceleration, or the rate of change of velocity. It is also important to introduce the idea of speed, which is the magnitude of velocity. Thus, we can state the following mathematical definitions.
Definition
Let \(s(t)\) be a function giving the position of an object at time t.
- The velocity of the object at time \(t\) is given by \(v(t)=s′(t)\).
- The speed of the object at time \(t\) is given by \(|v(t)|\).
- The acceleration of the object at \(t\) is given by \(a(t)=v′(t)=s''(t)\).
Example \(\PageIndex{2}\): Comparing Instantaneous Velocity and Average Velocity
A ball is dropped from a height of 64 feet. Its height above ground (in feet) \(t\) seconds later is given by \(s(t)=−16t^2+64\).
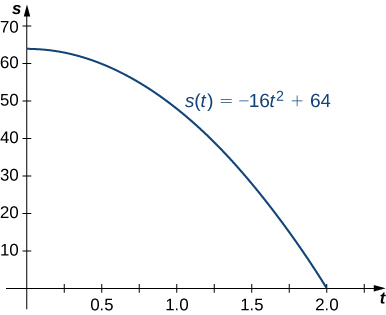
- What is the instantaneous velocity of the ball when it hits the ground?
- What is the average velocity during its fall?
Solution
The first thing to do is determine how long it takes the ball to reach the ground. To do this, set \(s(t)=0\). Solving \(−16t^2+64=0\), we get \(t=2\), so it take 2 seconds for the ball to reach the ground.
- The instantaneous velocity of the ball as it strikes the ground is \(v(2)\). Since \(v(t)=s′(t)=−32t\), we obtain \(v(t)=−64ft/s\).
- The average velocity of the ball during its fall is
\(v_{ave}=\frac{s(2)−s(0)}{2−0}=\frac{0−64}{2}=−32ft/s.\)
Example \(\PageIndex{3}\): Interpreting the Relationship between \(v(t)\) and \(a(t)\)
A particle moves along a coordinate axis in the positive direction to the right. Its position at time \(t\) is given by \(s(t)=t^3−4t+2\). Find \(v(1)\) and \(a(1)\) and use these values to answer the following questions.
- Is the particle moving from left to right or from right to left at time \(t=1\)?
- Is the particle speeding up or slowing down at time \(t=1\)?
Solution
Begin by finding \(v(t)\) and \(a(t)\). and \(a(t)=v′(t)=s''(t)=6t\).
Evaluating these functions at \(t=1)\), we obtain \(v(1)=−1\) and \(a(1)=6\).
- Because \(v(1)<0\), the particle is moving from right to left.
- Because \(v(1)<0\) and \(a(1)>0\), velocity and acceleration are acting in opposite directions. In other words, the particle is being accelerated in the direction opposite the direction in which it is traveling, causing |v(t)| to decrease. The particle is slowing down.
Example \(\PageIndex{4}\): Position and Velocity
The position of a particle moving along a coordinate axis is given by \(s(t)=t^3−9t^2+24t+4,t≥0.\)
- Find \(v(t)\).
- At what time(s) is the particle at rest?
- On what time intervals is the particle moving from left to right? From right to left?
- Use the information obtained to sketch the path of the particle along a coordinate axis.
Solution
a. The velocity is the derivative of the position function:
\(v(t)=s′(t)=3t^2−18t+24.\)
b. The particle is at rest when \(v(t)=0\), so set \(3t^2−18t+24=0\). Factoring the left-hand side of the equation produces \(3(t−2)(t−4)=0\). Solving, we find that the particle is at rest at \(t=2\) and \(t=4\).
c. The particle is moving from left to right when \(v(t)>0\) and from right to left when \(v(t)<0\). Figure gives the analysis of the sign of v(t) for t≥0, but it does not represent the axis along which the particle is moving.

Figure \(\PageIndex{2}\):The sign of \(v(t)\) determines the direction of the particle.
- Since \(3t^2−18t+24>0\) on \([0,2)∪(2,+∞)\), the particle is moving from left to right on these intervals.
- Since \(3t^2−18t+24<0\) on \((2,4)\), the particle is moving from right to left on this interval.
d. Before we can sketch the graph of the particle, we need to know its position at the time it starts moving \((t=0)\) and at the times that it changes direction \((t=2,4)\). We have \(s(0)=4,s(2)=24\), and \(s(4)=20\). This means that the particle begins on the coordinate axis at 4 and changes direction at 0 and 20 on the coordinate axis. The path of the particle is shown on a coordinate axis in Figure.
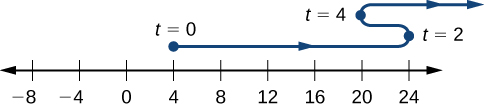
Figure \(\PageIndex{3}\): The path of the particle can be determined by analyzing \(v(t)\).
Exercise \(\PageIndex{2}\)
A particle moves along a coordinate axis. Its position at time t is given by \(s(t)=t^2−5t+1\). Is the particle moving from right to left or from left to right at time \(t=3\)?
- Hint
-
Find \(v(3)\) and look at the sign.
- Answer
-
left to right
EXAMPLE 3.2.63.2.6: FINDING ACCELERATION
The position of a particle along a coordinate axis at time tt (in seconds) is given by s(t)=3t2−4t+1s(t)=3t2−4t+1 (in meters). Find the function that describes its acceleration at time tt.
Solution
Since v(t)=s'(t)v(t)=s′(t) and a(t)=v'(t)=s′′(t)a(t)=v′(t)=s″(t), we begin by finding the derivative of s(t)s(t):
s'(t)=limh→0s(t+h)−s(t)hs′(t)=limh→0s(t+h)−s(t)h
=limh→03(t+h)2−4(t+h)+1−(3t2−4t+1)h=limh→03(t+h)2−4(t+h)+1−(3t2−4t+1)h
=6t−4.=6t−4.
Next,
s′′(t)=limh→0s'(t+h)−s'(t)hs″(t)=limh→0s′(t+h)−s′(t)h
=limh→06(t+h)−4−(6t−4)h=limh→06(t+h)−4−(6t−4)h
=6.=6.
Thus, a=6m/s2a=6m/s2.
EXERCISE 3.2.53.2.5
For s(t)=t3s(t)=t3, find a(t).a(t).
- Hint
- Answer
Population Change
In addition to analyzing velocity, speed, acceleration, and position, we can use derivatives to analyze various types of populations, including those as diverse as bacteria colonies and cities. We can use a current population, together with a growth rate, to estimate the size of a population in the future. The population growth rate is the rate of change of a population and consequently can be represented by the derivative of the size of the population.
Definition
If \(P(t)\) is the number of entities present in a population, then the population growth rate of \(P(t)\) is defined to be \(P′(t)\).
Example \(\PageIndex{5}\): Estimating a Population
The population of a city is tripling every 5 years. If its current population is 10,000, what will be its approximate population 2 years from now?
Solution
Let \(P(t)\) be the population (in thousands) \(t\) years from now. Thus, we know that \(P(0)=10\) and based on the information, we anticipate \(P(5)=30\). Now estimate \(P′(0)\), the current growth rate, using
\(P′(0)≈\frac{P(5)−P(0)}{5−0}=\frac{30−10}{5}=4\).
By applying Equation to \(P(t)\), we can estimate the population 2 years from now by writing
\(P(2)≈P(0)+(2)P′(0)≈10+2(4)=18\);
thus, in 2 years the population will be 18,000.
Exercise \(\PageIndex{3}\)
The current population of a mosquito colony is known to be 3,000; that is, \(P(0)=3,000\). If \(P′(0)=100\), estimate the size of the population in 3 days, where \(t\) is measured in days.
- Hint
-
Use \(P(3)≈P(0)+3P′(0)\)
- Answer
-
3,300
Changes in Cost and Revenue
In addition to analyzing motion along a line and population growth, derivatives are useful in analyzing changes in cost, revenue, and profit. The concept of a marginal function is common in the fields of business and economics and implies the use of derivatives. The marginal cost is the derivative of the cost function. The marginal revenue is the derivative of the revenue function. The marginal profit is the derivative of the profit function, which is based on the cost function and the revenue function.
Definition
- If \(C(x)\) is the cost of producing x items, then the marginal cost \(MC(x)\) is \(MC(x)=C′(x)\).
- If \(R(x)\) is the revenue obtained from selling x items, then the marginal revenue \(MR(x)\) is \(MR(x)=R′(x)\).
- If \(P(x)=R(x)−C(x)\) is the profit obtained from selling x items, then the marginal profit \(MP(x)\) is defined to be \(MP(x)=P′(x)=MR(x)−MC(x)=R′(x)−C′(x)\).
We can roughly approximate
\[MC(x)=C′(x)=\lim_{h→0}\frac{C(x+h)−C(x)}{h}\]
by choosing an appropriate value for \(h\). Since x represents objects, a reasonable and small value for \(h\) is 1. Thus, by substituting \(h=1\), we get the approximation \(MC(x)=C′(x)≈C(x+1)−C(x)\). Consequently, \(C′(x)\) for a given value of x can be thought of as the change in cost associated with producing one additional item. In a similar way, \(MR(x)=R′(x)\) approximates the revenue obtained by selling one additional item, and \(MP(x)=P′(x)\) approximates the profit obtained by producing and selling one additional item.
Example \(\PageIndex{6}\): Applying Marginal Revenue
Assume that the number of barbeque dinners that can be sold, \(x\), can be related to the price charged, \(p\), by the equation \(p(x)=9−0.03x,0≤x≤300\).
In this case, the revenue in dollars obtained by selling \(x\) barbeque dinners is given by
\(R(x)=xp(x)=x(9−0.03x)=−0.03x^2+9xfor0≤x≤300\).
Use the marginal revenue function to estimate the revenue obtained from selling the 101st barbeque dinner. Compare this to the actual revenue obtained from the sale of this dinner.
Solution
First, find the marginal revenue function: \(MR(x)=R′(x)=−0.06x+9.\)
Next, use \(R′(100)\) to approximate \(R(101)−R(100)\), the revenue obtained from the sale of the 101st dinner. Since \(R′(100)=3\), the revenue obtained from the sale of the 101st dinner is approximately $3.
The actual revenue obtained from the sale of the 101st dinner is
\(R(101)−R(100)=602.97−600=2.97,or$2.97\).
The marginal revenue is a fairly good estimate in this case and has the advantage of being easy to compute.
Exercise \(\PageIndex{4}\)
Suppose that the profit obtained from the sale of x fish-fry dinners is given by \(P(x)=−0.03x^2+8x−50\). Use the marginal profit function to estimate the profit from the sale of the 101st fish-fry dinner.
- Hint
-
Use \(P′(100)\) to approximate \(P(101)−P(100)\).
- Answer
-
$2
Key Concepts
- Using \(f(a+h)≈f(a)+f′(a)h\), it is possible to estimate \(f(a+h)\) given \(f′(a)\) and \(f(a)\).
- The rate of change of position is velocity, and the rate of change of velocity is acceleration. Speed is the absolute value, or magnitude, of velocity.
- The population growth rate and the present population can be used to predict the size of a future population.
- Marginal cost, marginal revenue, and marginal profit functions can be used to predict, respectively, the cost of producing one more item, the revenue obtained by selling one more item, and the profit obtained by producing and selling one more item.
Glossary
- acceleration
- is the rate of change of the velocity, that is, the derivative of velocity
- amount of change
- the amount of a function \(f(x)\) over an interval \([x,x+h] is f(x+h)−f(x)\)
- average rate of change
- is a function \(f(x)\) over an interval \([x,x+h]\) is \(\frac{f(x+h)−f(a)}{b−a}\)
- marginal cost
- is the derivative of the cost function, or the approximate cost of producing one more item
- marginal revenue
- is the derivative of the revenue function, or the approximate revenue obtained by selling one more item
- marginal profit
- is the derivative of the profit function, or the approximate profit obtained by producing and selling one more item
- population growth rate
- is the derivative of the population with respect to time
- speed
- is the absolute value of velocity, that is, \(|v(t)|\) is the speed of an object at time \(t\) whose velocity is given by \(v(t)\)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


