5.6: More U-Substitution - Exponential and Logarithmic Functions
- Last updated
- Save as PDF
- Page ID
- 20687
Exponential and logarithmic functions are used to model population growth, cell growth, and financial growth, as well as depreciation, radioactive decay, and resource consumption, to name only a few applications. In this section, we explore integration involving exponential and logarithmic functions.
Integrals of Exponential Functions
The exponential function is perhaps the most efficient function in terms of the operations of calculus. The exponential function, \(y=e^x\), is its own derivative and its own integral.
Rule: Integrals of Exponential Functions
Exponential functions can be integrated using the following formulas.
\[∫e^xdx=e^x+C\]
\[∫a^xdx=\dfrac{a^x}{\ln a}+C\]
Example \(\PageIndex{1}\): Finding an Antiderivative of an Exponential Function
Find the antiderivative of the exponential function \(e^{−x}\).
Solution: Use substitution, setting \(u=−x,\) and then \(du=−1dx\). Multiply the du equation by −1, so you now have \(−du=dx\). Then,
\(∫e^{−x}dx=−∫e^udu=−e^u+C=−e^{−x}+C.\)
Exercise \(\PageIndex{1}\)
Find the antiderivative of the function using substitution: \(x^2e^{−2x^3}\).
- Hint
-
Let u equal the exponent on e.
- Answer
-
\(∫x^2e^{−2x^3}dx=−\dfrac{1}{6}e^{−2x^3}+C\)
A common mistake when dealing with exponential expressions is treating the exponent on e the same way we treat exponents in polynomial expressions. We cannot use the power rule for the exponent on e. This can be especially confusing when we have both exponentials and polynomials in the same expression, as in the previous checkpoint. In these cases, we should always double-check to make sure we’re using the right rules for the functions we’re integrating.
Example \(\PageIndex{2}\): Square Root of an Exponential Function
Find the antiderivative of the exponential function \(e^x\sqrt{1+e^x}\).
Solution
First rewrite the problem using a rational exponent:
\(∫e^x\sqrt{1+e^x}dx=∫e^x(1+e^x)^{1/2}dx.\)
Using substitution, choose \(u=1+e^x.u=1+e^x\)Then, \(du=e^xdx\). We have (Figure)
\(∫e^x(1+e^x)^{1/2}dx=∫u^{1/2}du.\)
Then
\(∫u^{1/2}du=\dfrac{u^{3/2}}{3/2}+C=\dfrac{2}{3}u^{3/2}+C=\dfrac{2}{3}(1+e^x)^{3/2}+C\)
Figure \(\PageIndex{1}\): The graph shows an exponential function times the square root of an exponential function.
Exercise \(\PageIndex{2}\)
Find the antiderivative of \(e^x(3e^x−2)^2\).
- Hint
-
Let \(u=3e^x−2u=3e^x−2.\)
- Answer
-
\(∫e^x(3e^x−2)^2dx=\dfrac{1}{9}(3e^x−2)^3\)
Example \(\PageIndex{3}\): Using Substitution with an Exponential Function
Use substitution to evaluate the indefinite integral \(∫3x^2e^{2x^3}dx.\)
Solution
Here we choose to let u equal the expression in the exponent on e. Let \(u=2x^3\) and \(du=6x^2dx\).. Again, du is off by a constant multiplier; the original function contains a factor of \(3x^2,\) not \(6x^2\). Multiply both sides of the equation by \(\dfrac{1}{2}\) so that the integrand in u equals the integrand in x. Thus,
\(∫3x^2e^{2x^3}dx=\dfrac{1}{2}∫e^udu\).
Integrate the expression in u and then substitute the original expression in x back into the u integral:
\(\dfrac{1}{2}∫e^udu=\dfrac{1}{2}e^u+C=\dfrac{1}{2}e^2x^3+C.\)
Exercise \(\PageIndex{3}\)
Evaluate the indefinite integral \(∫2x^3ex^4dx\).
- Hint
-
Let \(u=x^4.\)
- Answer
-
\(∫2x^3ex^4dx=\dfrac{1}{2}e^{x^4}\)
As mentioned at the beginning of this section, exponential functions are used in many real-life applications. The number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative. Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth. Let’s look at an example in which integration of an exponential function solves a common business application.
A price–demand function tells us the relationship between the quantity of a product demanded and the price of the product. In general, price decreases as quantity demanded increases. The marginal price–demand function is the derivative of the price–demand function and it tells us how fast the price changes at a given level of production. These functions are used in business to determine the price–elasticity of demand, and to help companies determine whether changing production levels would be profitable.
Example \(\PageIndex{4}\): Finding a Price–Demand Equation
Find the price–demand equation for a particular brand of toothpaste at a supermarket chain when the demand is 50 tubes per week at $2.35 per tube, given that the marginal price—demand function, \(p′(x),\) for x number of tubes per week, is given as
\[p'(x)=−0.015e^{−0.01x}.\]
If the supermarket chain sells 100 tubes per week, what price should it set?
Solution
To find the price–demand equation, integrate the marginal price–demand function. First find the antiderivative, then look at the particulars. Thus,
\[p(x)=∫−0.015e^{−0.01x}dx=−0.015∫e^{−0.01x}dx.\]
Using substitution, let \(u=−0.01x\) and \(du=−0.01dx\). Then, divide both sides of the du equation by −0.01. This gives
\[\dfrac{−0.015}{−0.01}∫e^udu=1.5∫e^udu=1.5e^u+C=1.5e^{−0.01}x+C.\]
The next step is to solve for C. We know that when the price is $2.35 per tube, the demand is 50 tubes per week. This means
\[p(50)=1.5e^{−0.01(50)}+C=2.35.\]
Now, just solve for C:
\[C=2.35−1.5e^{−0.5}=2.35−0.91=1.44.\]
Thus,
\[p(x)=1.5e^{−0.01x}+1.44.\]
If the supermarket sells 100 tubes of toothpaste per week, the price would be
\[p(100)=1.5e−0.01(100)+1.44=1.5e−1+1.44≈1.99.\]
The supermarket should charge $1.99 per tube if it is selling 100 tubes per week.
Example \(\PageIndex{5}\): Evaluating a Definite Integral Involving an Exponential Function
Evaluate the definite integral \[∫^2_1e^{1−x}dx.\]
Solution
Again, substitution is the method to use. Let \(u=1−x,\) so \(du=−1dx\) or \(−du=dx\). Then \(∫e^{1−x}dx=−∫e^udu.\) Next, change the limits of integration. Using the equation \(u=1−x\), we have
\[u=1−(1)=0\]
\[u=1−(2)=−1.\]
The integral then becomes
\[∫^2_1e^{1−x}\,dx=−∫^{−1}_0e^u\,du=∫^0_{−1}e^u\,du=eu|^0_{−1}=e^0−(e^{−1})=−e^{−1}+1.\]
See Figure.
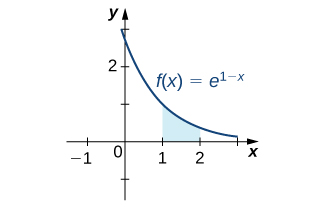
Figure \(\PageIndex{2}\): The indicated area can be calculated by evaluating a definite integral using substitution.
Exercise \(\PageIndex{4}\)
Evaluate \(∫^2_0e^{2x}dx.\)
- Hint
-
Let \(u=2x.\)
- Answer
-
\(\dfrac{1}{2}∫^4_0e^udu=\dfrac{1}{2}(e^4−1)\)
Example \(\PageIndex{6}\): Growth of Bacteria in a Culture
Suppose the rate of growth of bacteria in a Petri dish is given by \(q(t)=3^t\), where t is given in hours and \(q(t)\) is given in thousands of bacteria per hour. If a culture starts with 10,000 bacteria, find a function \(Q(t)\) that gives the number of bacteria in the Petri dish at any time t. How many bacteria are in the dish after 2 hours?
Solution
We have
\[Q(t)=∫3^tdt=\dfrac{3^t}{\ln 3}+C.\]
Then, at \(t=0\) we have \(Q(0)=10=\dfrac{1}{\ln 3}+C,\) so \(C≈9.090\) and we get
\[Q(t)=\dfrac{3^t}{\ln 3}+9.090.\]
At time \(t=2\), we have
\[Q(2)=\dfrac{3^2}{\ln 3}+9.090\]
\[=17.282.\]
After 2 hours, there are 17,282 bacteria in the dish.
Exercise \(\PageIndex{5}\)
From Example, suppose the bacteria grow at a rate of \(q(t)=2^t\). Assume the culture still starts with 10,000 bacteria. Find \(Q(t)\). How many bacteria are in the dish after 3 hours?
- Hint
-
Use the procedure from Example to solve the problem
- Answer
-
\(Q(t)=\dfrac{2^t}{\ln 2}+8.557.\) There are 20,099 bacteria in the dish after 3 hours.
Example \(\PageIndex{7}\): Fruit Fly Population Growth
Suppose a population of fruit flies increases at a rate of \(g(t)=2e^{0.02t}\), in flies per day. If the initial population of fruit flies is 100 flies, how many flies are in the population after 10 days?
Solution
Let \(G(t)\) represent the number of flies in the population at time t. Applying the net change theorem, we have
\(G(10)=G(0)+∫^{10}_02e^{0.02t}dt\)
\(=100+[\dfrac{2}{0.02}e^{0.02t}]∣^{10}_0\)
\(=100+[100e^{0.02t}]∣^{10}_0\)
\(=100+100e^{0.2}−100\)
\(≈122.\)
There are 122 flies in the population after 10 days.
Exercise \(\PageIndex{6}\)
Suppose the rate of growth of the fly population is given by \(g(t)=e^{0.01t},\) and the initial fly population is 100 flies. How many flies are in the population after 15 days?
- Hint
-
Use the process from Example to solve the problem.
- Answer
-
There are 116 flies.
Example \(\PageIndex{8}\): Evaluating a Definite Integral Using Substitution
Evaluate the definite integral using substitution: \[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx.\]
Solution
This problem requires some rewriting to simplify applying the properties. First, rewrite the exponent on e as a power of x, then bring the \(x^2\) in the denominator up to the numerator using a negative exponent. We have
\[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx=∫^2_1e^{x^{−1}}x^{−2}\,dx.\]
Let \(u=x^{−1},\) the exponent on \(e\). Then
\[du=−x^{−2}\,dx\]
\[−du=x^{−2}\,dx.\]
Bringing the negative sign outside the integral sign, the problem now reads
\[−∫e^u\,du.\]
Next, change the limits of integration:
\[u=(1)^{−1}=1\]
\[u=(2)^{−1}=\dfrac{1}{2}.\]
Notice that now the limits begin with the larger number, meaning we must multiply by −1 and interchange the limits. Thus,
\[−∫^{1/2}_1e^udu=∫^1_{1/2}e^udu=e^u|^1_{1/2}=e−e^{1/2}=e−\sqrt{e}.\]
Exercise \(\PageIndex{7}\)
Evaluate the definite integral using substitution: \[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}dx.\]
- Hint
-
Let \(u=4x^{−2}.\)
- Answer
-
\[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}dx=\dfrac{1}{8}[e^4−e]\].
Integrals Involving Logarithmic Functions
Integrating functions of the form \(f(x)=x^{−1}\) result in the absolute value of the natural log function, as shown in the following rule. Integral formulas for other logarithmic functions, such as \(f(x)=\ln x\) and \(f(x)=log_ax\), are also included in the rule.
Rule: Integration Formulas Involving Logarithmic Functions
The following formulas can be used to evaluate integrals involving logarithmic functions.
\[\begin{align} ∫x^{−1}dx &=\ln |x|+C \\ ∫\ln x\,dx &= x\ln x−x+C =x (\ln x−1)+C \\ ∫log_a\,x\,dx &=\dfrac{x}{\ln a}(\ln x−1)+C \end{align}\]
Example \(\PageIndex{9}\): Finding an Antiderivative Involving \(\ln x\)
Find the antiderivative of the function \[\dfrac{3}{x−10}.\]
Solution
First factor the 3 outside the integral symbol. Then use the \(u^{−1}\) rule. Thus,
\[∫\dfrac{3}{x−10}dx=3∫\dfrac{1}{x−10}dx=3∫\dfrac{du}{u}=3\ln |u|+C=3\ln |x−10|+C,x≠10.\]
See Figure.
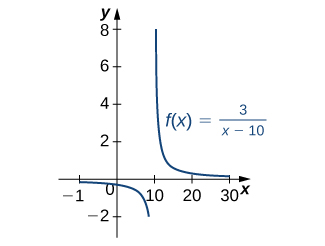
Figure \(\PageIndex{3}\): The domain of this function is \(x \neq 10.\)
Exercise \(\PageIndex{8}\)
Find the antiderivative of \[\dfrac{1}{x+2}.\]
- Hint
-
Follow the pattern from Example to solve the problem.
- Answer
-
\[\ln |x+2|+C\]
Example \(\PageIndex{10}\): Finding an Antiderivative of a Rational Function
Find the antiderivative of \[\dfrac{2x^3+3x}{x^4+3x^2}.\]
Solution
This can be rewritten as \(∫(2x^3+3x)(x^4+3x^2)^{−1}dx.\) Use substitution. Let \(u=x^4+3x^2\), then \(du=4x^3+6x.\) Alter du by factoring out the 2. Thus,
\[du=(4x^3+6x)dx=2(2x^3+3x)dx\]
\[\dfrac{1}{2}du=(2x^3+3x)dx.\]
Rewrite the integrand in u:
\[∫(2x^3+3x)(x^4+3x^2)^{−1}dx=\dfrac{1}{2}∫u^{−1}du.\]
Then we have
\[\dfrac{1}{2}∫u^{−1}du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln ∣x^4+3x^2∣+C.\]
Example \(\PageIndex{11}\): Finding an Antiderivative of a Logarithmic Function
Find the antiderivative of the log function \[log_2x.\)
Solution
Follow the format in the formula listed in the rule on integration formulas involving logarithmic functions. Based on this format, we have
\[∫log_2xdx=\dfrac{x}{\ln 2}(\ln x−1)+C.\]
Exercise \(\PageIndex{9}\)
Find the antiderivative of \(log_3x\).
- Hint
-
Follow Example and refer to the rule on integration formulas involving logarithmic functions.
- Answer
-
\[\dfrac{x}{\ln 3}(\ln x−1)+C\]
Example is a definite integral of a trigonometric function. With trigonometric functions, we often have to apply a trigonometric property or an identity before we can move forward. Finding the right form of the integrand is usually the key to a smooth integration.
Example \(\PageIndex{12}\): Evaluating a Definite Integral
Find the definite integral of \[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}dx.\]
Solution
We need substitution to evaluate this problem. Let \(u=1+\cos x\) so \(du=−\sin x\,dx.\) Rewrite the integral in terms of u, changing the limits of integration as well. Thus,
\[u=1+cos(0)=2\]
\[u=1+cos(\dfrac{π}{2})=1.\]
Then
\[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}=−∫^1+2u^{−1}du=∫^2_1u^{−1}du=\ln |u|^2_1=[\ln 2−\ln 1]=\ln 2\]
Key Concepts
- Exponential and logarithmic functions arise in many real-world applications, especially those involving growth and decay.
- Substitution is often used to evaluate integrals involving exponential functions or logarithms.
Key Equations
- Integrals of Exponential Functions
\(∫e^xdx=e^x+C\)
\(∫a^xdx=\dfrac{a^x}{\ln a}+C\)
- Integration Formulas Involving Logarithmic Functions
\(∫x^{−1}dx=\ln |x|+C\)
\(∫\ln xdx=x\ln x−x+C=x(\ln x−1)+C\)
\(∫log_axdx=\dfrac{x}{\ln a}(\ln x−1)+C\)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


