Chapter 1 Review Exercises
- Last updated
- Save as PDF
- Page ID
- 30358
Chapter Review Exercises
Introduction to Whole Numbers
Use Place Value with Whole Number
In the following exercises find the place value of each digit.
Exercise \(\PageIndex{1}\)
26,915
- 1
- 2
- 9
- 5
- 6
- Answer
-
- tens
- ten thousands
- hundreds
- ones
- thousands
Exercise \(\PageIndex{2}\)
359,417
- 9
- 3
- 4
- 7
- 1
Exercise \(\PageIndex{3}\)
58,129,304
- 5
- 0
- 1
- 8
- 2
- Answer
-
- ten millions
- tens
- hundred thousands
- millions
- ten thousands
Exercise \(\PageIndex{4}\)
9,430,286,157
- 6
- 4
- 9
- 0
- 5
In the following exercises, name each number.
Exercise \(\PageIndex{5}\)
6,104
- Answer
-
six thousand, one hundred four
Exercise \(\PageIndex{6}\)
493,068
Exercise \(\PageIndex{7}\)
3,975,284
- Answer
-
three million, nine hundred seventy-five thousand, two hundred eighty-four
Exercise \(\PageIndex{8}\)
85,620,435
In the following exercises, write each number as a whole number using digits.
Exercise \(\PageIndex{9}\)
three hundred fifteen
- Answer
-
315
Exercise \(\PageIndex{10}\)
sixty-five thousand, nine hundred twelve
Exercise \(\PageIndex{11}\)
ninety million, four hundred twenty-five thousand, sixteen
- Answer
-
90,425,016
Exercise \(\PageIndex{12}\)
one billion, forty-three million, nine hundred twenty-two thousand, three hundred eleven
In the following exercises, round to the indicated place value.
Exercise \(\PageIndex{13}\)
Round to the nearest ten.
- 407
- 8,564
- Answer
-
- 410
- 8,560
Exercise \(\PageIndex{14}\)
Round to the nearest hundred.
- 25,846
- 25,864
In the following exercises, round each number to the nearest 1. hundred 2. thousand 3. ten thousand.
Exercise \(\PageIndex{15}\)
864,951
- Answer
-
- 865,000865,000
- 865,000865,000
- 860,000
Exercise \(\PageIndex{16}\)
3,972,849
Identify Multiples and Factors
In the following exercises, use the divisibility tests to determine whether each number is divisible by 2, by 3, by 5, by 6, and by 10.
Exercise \(\PageIndex{17}\)
168
- Answer
-
by 2,3,6
Exercise \(\PageIndex{18}\)
264
Exercise \(\PageIndex{19}\)
375
- Answer
-
by 3,5
Exercise \(\PageIndex{20}\)
750
Exercise \(\PageIndex{21}\)
1430
- Answer
-
by 2,5,10
Exercise \(\PageIndex{22}\)
1080
Find Prime Factorizations and Least Common Multiples
In the following exercises, find the prime factorization.
Exercise \(\PageIndex{23}\)
420
- Answer
-
2\(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)
Exercise \(\PageIndex{24}\)
115
Exercise \(\PageIndex{25}\)
225
- Answer
-
3\(\cdot 3 \cdot 5 \cdot 5\)
Exercise \(\PageIndex{26}\)
2475
Exercise \(\PageIndex{27}\)
1560
- Answer
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)
Exercise \(\PageIndex{28}\)
56
Exercise \(\PageIndex{29}\)
72
- Answer
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)
Exercise \(\PageIndex{30}\)
168
Exercise \(\PageIndex{31}\)
252
- Answer
-
\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
Exercise \(\PageIndex{32}\)
391
In the following exercises, find the least common multiple of the following numbers using the multiples method.
Exercise \(\PageIndex{33}\)
6,15
- Answer
-
30
Exercise \(\PageIndex{34}\)
60, 75
In the following exercises, find the least common multiple of the following numbers using the prime factors method.
Exercise \(\PageIndex{35}\)
24, 30
- Answer
-
120
Exercise \(\PageIndex{36}\)
70, 84
Use the Language of Algebra
Use Variables and Algebraic Symbols
In the following exercises, translate the following from algebra to English.
Exercise \(\PageIndex{37}\)
25−7
- Answer
-
25 minus 7, the difference of twenty-five and seven
Exercise \(\PageIndex{38}\)
5\(\cdot 6\)
Exercise \(\PageIndex{39}\)
\(45 \div 5\)
- Answer
-
45 divided by 5, the quotient of forty-five and five
Exercise \(\PageIndex{40}\)
x+8
Exercise \(\PageIndex{41}\)
\(42 \geq 27\)
- Answer
-
forty-two is greater than or equal to twenty-seven
Exercise \(\PageIndex{42}\)
3n=24
Exercise \(\PageIndex{43}\)
\(3 \leq 20 \div 4\)
- Answer
-
3 is less than or equal to 20 divided by 4, three is less than or equal to the quotient of twenty and four
Exercise \(\PageIndex{44}\)
\(a \neq 7 \cdot 4\)
In the following exercises, determine if each is an expression or an equation.
Exercise \(\PageIndex{45}\)
\(6 \cdot 3+5\)
- Answer
-
expression
Exercise \(\PageIndex{46}\)
y−8=32
Simplify Expressions Using the Order of Operations
In the following exercises, simplify each expression.
Exercise \(\PageIndex{47}\)
\(3^{5}\)
- Answer
-
243
Exercise \(\PageIndex{48}\)
\(10^{8}\)
In the following exercises, simplify
Exercise \(\PageIndex{49}\)
6+10/2+2
- Answer
-
13
Exercise \(\PageIndex{50}\)
9+12/3+4
Exercise \(\PageIndex{51}\)
\(20 \div(4+6) \cdot 5\)
- Answer
-
10
Exercise \(\PageIndex{52}\)
\(33 \div(3+8) \cdot 2\)
Exercise \(\PageIndex{53}\)
\(4^{2}+5^{2}\)
- Answer
-
41
Exercise \(\PageIndex{54}\)
\((4+5)^{2}\)
Evaluate an Expression
In the following exercises, evaluate the following expressions.
Exercise \(\PageIndex{55}\)
9x+7 when x=3
- Answer
-
34
Exercise \(\PageIndex{56}\)
5x−4 when x=6
Exercise \(\PageIndex{57}\)
\(x^{4}\) when \(x=3\)
- Answer
-
81
Exercise \(\PageIndex{58}\)
\(3^{x}\) when \(x=3\)
Exercise \(\PageIndex{59}\)
\(x^{2}+5 x-8\) when \(x=6\)
- Answer
-
58
Exercise \(\PageIndex{60}\)
\(2 x+4 y-5\) when
\(x=7, y=8\)
Simplify Expressions by Combining Like Terms
In the following exercises, identify the coefficient of each term.
Exercise \(\PageIndex{61}\)
12n
- Answer
-
12
Exercise \(\PageIndex{62}\)
9\(x^{2}\)
In the following exercises, identify the like terms.
Exercise \(\PageIndex{63}\)
\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)
- Answer
-
12 and \(3, n^{2}\) and 3\(n^{2}\)
Exercise \(\PageIndex{64}\)
\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)
In the following exercises, identify the terms in each expression.
Exercise \(\PageIndex{65}\)
\(11 x^{2}+3 x+6\)
- Answer
-
\(11 x^{2}, 3 x, 6\)
Exercise \(\PageIndex{66}\)
\(22 y^{3}+y+15\)
In the following exercises, simplify the following expressions by combining like terms.
Exercise \(\PageIndex{67}\)
17a+9a
- Answer
-
26a
Exercise \(\PageIndex{68}\)
18z+9z
Exercise \(\PageIndex{69}\)
9x+3x+8
- Answer
-
12x+8
Exercise \(\PageIndex{70}\)
8a+5a+9
Exercise \(\PageIndex{71}\)
7p+6+5p−4
- Answer
-
12p+2
Exercise \(\PageIndex{72}\)
8x+7+4x−5
Translate an English Phrase to an Algebraic Expression
In the following exercises, translate the following phrases into algebraic expressions.
Exercise \(\PageIndex{73}\)
the sum of 8 and 12
- Answer
-
8+12
Exercise \(\PageIndex{74}\)
the sum of 9 and 1
Exercise \(\PageIndex{75}\)
the difference of x and 4
- Answer
-
x−4
Exercise \(\PageIndex{76}\)
the difference of x and 3
Exercise \(\PageIndex{77}\)
the product of 6 and y
- Answer
-
6y
Exercise \(\PageIndex{78}\)
the product of 9 and y
Exercise \(\PageIndex{79}\)
Adele bought a skirt and a blouse. The skirt cost $15 more than the blouse. Let bb represent the cost of the blouse. Write an expression for the cost of the skirt.
- Answer
-
b+15
Exercise \(\PageIndex{80}\)
Marcella has 6 fewer boy cousins than girl cousins. Let g represent the number of girl cousins. Write an expression for the number of boy cousins.
Add and Subtract Integers
Use Negatives and Opposites of Integers
In the following exercises, order each of the following pairs of numbers, using < or >.
Exercise \(\PageIndex{81}\)
- 6___2
- −7___4
- −9___−1
- 9___−3
- Answer
-
- >
- <
- <
- >
Exercise \(\PageIndex{82}\)
- −5___1
- −4___−9
- 6___10
- 3___−8
In the following exercises,, find the opposite of each number.
Exercise \(\PageIndex{83}\)
- −8
- 1
- Answer
-
- 8
- −1
Exercise \(\PageIndex{84}\)
- −2
- 6
In the following exercises, simplify.
Exercise \(\PageIndex{85}\)
−(−19)
- Answer
-
19
Exercise \(\PageIndex{86}\)
−(−53)
In the following exercises, simplify.
Exercise \(\PageIndex{87}\)
−m when
- m=3
- m=−3
- Answer
-
- −3
- 3
Exercise \(\PageIndex{88}\)
−p when
- p=6
- p=−6
Simplify Expressions with Absolute Value
In the following exercises,, simplify.
Exercise \(\PageIndex{89}\)
- |7|
- |−25|
- |0|
- Answer
-
- 7
- 25
- 0
Exercise \(\PageIndex{90}\)
- |5|
- |0|
- |−19|
In the following exercises, fill in <, >, or = for each of the following pairs of numbers.
Exercise \(\PageIndex{91}\)
- −8___|−8|
- −|−2|___−2
- Answer
-
- <
- =
Exercise \(\PageIndex{92}\)
- |−3|___−|−3|
- 4___−|−4|
In the following exercises, simplify.
Exercise \(\PageIndex{93}\)
|8−4|
- Answer
-
4
Exercise \(\PageIndex{94}\)
|9−6|
Exercise \(\PageIndex{95}\)
8(14−2|−2|)
- Answer
-
80
Exercise \(\PageIndex{96}\)
6(13−4|−2|)
In the following exercises, evaluate.
Exercise \(\PageIndex{97}\)
1. |x| when x=−28
- Answer
-
- 28
- 15
Exercise \(\PageIndex{98}\)
- ∣y∣ when y=−37
- |−z| when z=−24
Add Integers
In the following exercises, simplify each expression.
Exercise \(\PageIndex{99}\)
−200+65
- Answer
-
−135
Exercise \(\PageIndex{100}\)
−150+45
Exercise \(\PageIndex{101}\)
2+(−8)+6
- Answer
-
0
Exercise \(\PageIndex{102}\)
4+(−9)+7
Exercise \(\PageIndex{103}\)
140+(−75)+67
- Answer
-
132
Exercise \(\PageIndex{104}\)
−32+24+(−6)+10
Subtract Integers
In the following exercises, simplify.
Exercise \(\PageIndex{105}\)
9−3
- Answer
-
6
Exercise \(\PageIndex{106}\)
−5−(−1)
Exercise \(\PageIndex{107}\)
- 15−6
- 15+(−6)
- Answer
-
- 9
- 9
Exercise \(\PageIndex{108}\)
- 12−9
- 12+(−9)
Exercise \(\PageIndex{109}\)
- 8−(−9)
- 8+9
- Answer
-
- 17
- 17
Exercise \(\PageIndex{110}\)
- 4−(−4)
- 4+4
In the following exercises, simplify each expression.
Exercise \(\PageIndex{111}\)
10−(−19)
- Answer
-
29
Exercise \(\PageIndex{112}\)
11−(−18)
Exercise \(\PageIndex{113}\)
31−79
- Answer
-
−48
Exercise \(\PageIndex{114}\)
39−81
Exercise \(\PageIndex{115}\)
−31−11
- Answer
-
−42
Exercise \(\PageIndex{116}\)
−32−18
Exercise \(\PageIndex{117}\)
−15−(−28)+5
- Answer
-
18
Exercise \(\PageIndex{118}\)
71+(−10)−8
Exercise \(\PageIndex{119}\)
−16−(−4+1)−7
- Answer
-
-20
Exercise \(\PageIndex{120}\)
−15−(−6+4)−3
Multiply Integers
In the following exercises, multiply.
Exercise \(\PageIndex{121}\)
−5(7)
- Answer
-
−35
Exercise \(\PageIndex{122}\)
−8(6)
Exercise \(\PageIndex{123}\)
−18(−2)
- Answer
-
36
Exercise \(\PageIndex{124}\)
−10(−6)
Divide Integers
In the following exercises, divide.
Exercise \(\PageIndex{125}\)
\(-28 \div 7\)
- Answer
-
-4
Exercise \(\PageIndex{126}\)
\(56 \div(-7)\)
Exercise \(\PageIndex{127}\)
\(-120 \div(-20)\)
- Answer
-
6
Exercise \(\PageIndex{128}\)
\(-200 \div 25\)
Simplify Expressions with Integers
In the following exercises, simplify each expression.
Exercise \(\PageIndex{129}\)
−8(−2)−3(−9)
- Answer
-
43
Exercise \(\PageIndex{130}\)
−7(−4)−5(−3)
Exercise \(\PageIndex{131}\)
\((-5)^{3}\)
- Answer
-
−125
Exercise \(\PageIndex{132}\)
\((-4)^{3}\)
Exercise \(\PageIndex{133}\)
\(-4 \cdot 2 \cdot 11\)
- Answer
-
−88
Exercise \(\PageIndex{134}\)
\(-5 \cdot 3 \cdot 10\)
Exercise \(\PageIndex{135}\)
\(-10(-4) \div(-8)\)
- Answer
-
-5
Exercise \(\PageIndex{136}\)
\(-8(-6) \div(-4)\)
Exercise \(\PageIndex{137}\)
31−4(3−9)
- Answer
-
55
Exercise \(\PageIndex{138}\)
24−3(2−10)
Evaluate Variable Expressions with Integers
In the following exercises, evaluate each expression.
Exercise \(\PageIndex{139}\)
x+8 when
- x=−26
- x=−95
- Answer
-
- −18
- −87
Exercise \(\PageIndex{140}\)
y+9 when
- y=−29
- y=−84
Exercise \(\PageIndex{141}\)
When b=−11, evaluate:
- b+6
- −b+6
- Answer
-
- −5
- 17
Exercise \(\PageIndex{142}\)
When c=−9, evaluate:
- c+(−4)c+(−4)
- −c+(−4)
Exercise \(\PageIndex{143}\)
\(p^{2}-5 p+2\) when
\(p=-1\)
- Answer
-
8
Exercise \(\PageIndex{144}\)
\(q^{2}-2 q+9\) when \(q=-2\)
Exercise \(\PageIndex{145}\)
\(6 x-5 y+15\) when \(x=3\) and \(y=-1\)
- Answer
-
38
Exercise \(\PageIndex{146}\)
\(3 p-2 q+9\) when \(p=8\) and \(q=-2\)
Translate English Phrases to Algebraic Expressions
In the following exercises, translate to an algebraic expression and simplify if possible.
Exercise \(\PageIndex{147}\)
the sum of −4 and −17, increased by 32
- Answer
-
(−4+(−17))+32;11
Exercise \(\PageIndex{148}\)
- the difference of 15 and −7
- subtract 15 from −7
Exercise \(\PageIndex{149}\)
the quotient of −45 and −9
- Answer
-
\(\frac{-45}{-9} ; 5\)
Exercise \(\PageIndex{150}\)
the product of −12 and the difference of c and d
Use Integers in Applications
In the following exercises, solve.
Exercise \(\PageIndex{151}\)
Temperature The high temperature one day in Miami Beach, Florida, was 76°. That same day, the high temperature in Buffalo, New York was −8°. What was the difference between the temperature in Miami Beach and the temperature in Buffalo?
- Answer
-
84 degrees
Exercise \(\PageIndex{152}\)
Checking Account Adrianne has a balance of −$22 in her checking account. She deposits $301 to the account. What is the new balance?
Visualize Fractions
Find Equivalent Fractions
In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.
Exercise \(\PageIndex{153}\)
\(\frac{1}{4}\)
- Answer
-
\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\) answers may vary
Exercise \(\PageIndex{154}\)
\(\frac{1}{3}\)
Exercise \(\PageIndex{155}\)
\(\frac{5}{6}\)
- Answer
-
\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\) answers may vary
Exercise \(\PageIndex{156}\)
\(\frac{2}{7}\)
Simplify Fractions
In the following exercises, simplify.
Exercise \(\PageIndex{157}\)
\(\frac{7}{21}\)
- Answer
-
\(\frac{1}{3}\)
Exercise \(\PageIndex{158}\)
\(\frac{8}{24}\)
Exercise \(\PageIndex{159}\)
\(\frac{15}{20}\)
- Answer
-
\(\frac{3}{4}\)
Exercise \(\PageIndex{160}\)
\(\frac{12}{18}\)
Exercise \(\PageIndex{161}\)
\(-\frac{168}{192}\)
- Answer
-
\(-\frac{7}{8}\)
Exercise \(\PageIndex{162}\)
\(-\frac{140}{224}\)
Exercise \(\PageIndex{163}\)
\(\frac{11 x}{11 y}\)
- Answer
-
\(\frac{x}{y}\)
Exercise \(\PageIndex{164}\)
\(\frac{15 a}{15 b}\)
Multiply Fractions
In the following exercises, multiply.
Exercise \(\PageIndex{165}\)
\(\frac{2}{5} \cdot \frac{1}{3}\)
- Answer
-
\(\frac{2}{15}\)
Exercise \(\PageIndex{166}\)
\(\frac{1}{2} \cdot \frac{3}{8}\)
Exercise \(\PageIndex{167}\)
\(\frac{7}{12}\left(-\frac{8}{21}\right)\)
- Answer
-
\(-\frac{2}{9}\)
Exercise \(\PageIndex{168}\)
\(\frac{5}{12}\left(-\frac{8}{15}\right)\)
Exercise \(\PageIndex{169}\)
\(-28 p\left(-\frac{1}{4}\right)\)
- Answer
-
7p
Exercise \(\PageIndex{170}\)
\(-51 q\left(-\frac{1}{3}\right)\)
Exercise \(\PageIndex{172}\)
\(\frac{14}{5}(-15)\)
- Answer
-
−42
Exercise \(\PageIndex{173}\)
\(-1\left(-\frac{3}{8}\right)\)
Divide Fractions
In the following exercises, divide
Exercise \(\PageIndex{174}\)
\(\frac{1}{2} \div \frac{1}{4}\)
- Answer
-
2
Exercise \(\PageIndex{175}\)
\(\frac{1}{2} \div \frac{1}{8}\)
Exercise \(\PageIndex{176}\)
\(-\frac{4}{5} \div \frac{4}{7}\)
- Answer
-
\(-\frac{7}{5}\)
Exercise \(\PageIndex{177}\)
\(-\frac{3}{4} \div \frac{3}{5}\)
Exercise \(\PageIndex{178}\)
\(\frac{5}{8} \div \frac{a}{10}\)
- Answer
-
\(\frac{25}{4 a}\)
Exercise \(\PageIndex{179}\)
\(\frac{5}{6} \div \frac{c}{15}\)
Exercise \(\PageIndex{180}\)
\(\frac{7 p}{12} \div \frac{21 p}{8}\)
- Answer
-
\(\frac{2}{9}\)
Exercise \(\PageIndex{181}\)
\(\frac{5 q}{12} \div \frac{15 q}{8}\)
Exercise \(\PageIndex{182}\)
\(\frac{2}{5} \div(-10)\)
- Answer
-
\(-\frac{1}{25}\)
Exercise \(\PageIndex{183}\)
\(-18 \div-\left(\frac{9}{2}\right)\)
In the following exercises, simplify.
Exercise \(\PageIndex{184}\)
\(\frac{\frac{2}{3}}{\frac{8}{9}}\)
- Answer
-
\(\frac{3}{4}\)
Exercise \(\PageIndex{185}\)
\(\frac{\frac{4}{5}}{\frac{8}{15}}\)
Exercise \(\PageIndex{186}\)
\(\frac{-\frac{9}{10}}{3}\)
- Answer
-
\(-\frac{3}{10}\)
Exercise \(\PageIndex{187}\)
\(\frac{2}{\frac{5}{8}}\)
Exercise \(\PageIndex{188}\)
\(\frac{\frac{r}{5}}{\frac{s}{3}}\)
- Answer
-
\(\frac{3 r}{5 s}\)
Exercise \(\PageIndex{189}\)
\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)
Simplify Expressions Written with a Fraction Bar
In the following exercises, simplify.
Exercise \(\PageIndex{190}\)
\(\frac{4+11}{8}\)
- Answer
-
\(\frac{15}{8}\)
Exercise \(\PageIndex{191}\)
\(\frac{9+3}{7}\)
Exercise \(\PageIndex{192}\)
\(\frac{30}{7-12}\)
- Answer
-
-6
Exercise \(\PageIndex{193}\)
\(\frac{15}{4-9}\)
Exercise \(\PageIndex{194}\)
\(\frac{22-14}{19-13}\)
- Answer
-
\(\frac{4}{3}\)
Exercise \(\PageIndex{195}\)
\(\frac{15+9}{18+12}\)
Exercise \(\PageIndex{196}\)
\(\frac{5 \cdot 8}{-10}\)
- Answer
-
-4
Exercise \(\PageIndex{197}\)
\(\frac{3 \cdot 4}{-24}\)
Exercise \(\PageIndex{198}\)
\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)
- Answer
-
\(\frac{5}{2}\)
Exercise \(\PageIndex{199}\)
\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)
Exercise \(\PageIndex{200}\)
\(\frac{2+4(3)}{-3-2^{2}}\)
- Answer
-
-2
Exercise \(\PageIndex{201}\)
\(\frac{7+3(5)}{-2-3^{2}}\)
Translate Phrases to Expressions with Fractions
In the following exercises, translate each English phrase into an algebraic expression.
Exercise \(\PageIndex{202}\)
the quotient of c and the sum of d and 9.
- Answer
-
\(\frac{c}{d+9}\)
Exercise \(\PageIndex{203}\)
the quotient of the difference of h and k, and −5.
Add and Subtract Fractions
Add and Subtract Fractions with a Common Denominator
In the following exercises, add.
Exercise \(\PageIndex{204}\)
\(\frac{4}{9}+\frac{1}{9}\)
- Answer
-
\(\frac{5}{9}\)
Exercise \(\PageIndex{205}\)
\(\frac{2}{9}+\frac{5}{9}\)
Exercise \(\PageIndex{206}\)
\(\frac{y}{3}+\frac{2}{3}\)
- Answer
-
\(\frac{y+2}{3}\)
Exercise \(\PageIndex{207}\)
\(\frac{7}{p}+\frac{9}{p}\)
Exercise \(\PageIndex{208}\)
\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)
- Answer
-
\(-\frac{1}{2}\)
Exercise \(\PageIndex{209}\)
\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)
In the following exercises, subtract.
Exercise \(\PageIndex{210}\)
\(\frac{4}{5}-\frac{1}{5}\)
- Answer
-
\(\frac{3}{5}\)
Exercise \(\PageIndex{211}\)
\(\frac{4}{5}-\frac{3}{5}\)
Exercise \(\PageIndex{212}\)
\(\frac{y}{17}-\frac{9}{17}\)
- Answer
-
\(\frac{y-9}{17}\)
Exercise \(\PageIndex{213}\)
\(\frac{x}{19}-\frac{8}{19}\)
Exercise \(\PageIndex{214}\)
\(-\frac{8}{d}-\frac{3}{d}\)
- Answer
-
\(-\frac{11}{d}\)
Exercise \(\PageIndex{215}\)
\(-\frac{7}{c}-\frac{7}{c}\)
Add or Subtract Fractions with Different Denominators
In the following exercises, add or subtract.
Exercise \(\PageIndex{216}\)
\(\frac{1}{3}+\frac{1}{5}\)
- Answer
-
\(\frac{8}{15}\)
Exercise \(\PageIndex{217}\)
\(\frac{1}{4}+\frac{1}{5}\)
Exercise \(\PageIndex{218}\)
\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)
- Answer
-
\(\frac{3}{10}\)
Exercise \(\PageIndex{219}\)
\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)
Exercise \(\PageIndex{220}\)
\(\frac{2}{3}+\frac{3}{4}\)
- Answer
-
\(\frac{17}{12}\)
Exercise \(\PageIndex{221}\)
\(\frac{3}{4}+\frac{2}{5}\)
Exercise \(\PageIndex{222}\)
\(\frac{11}{12}-\frac{3}{8}\)
- Answer
-
\(\frac{13}{24}\)
Exercise \(\PageIndex{223}\)
\(\frac{5}{8}-\frac{7}{12}\)
Exercise \(\PageIndex{224}\)
\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)
- Answer
-
\(\frac{19}{80}\)
Exercise \(\PageIndex{225}\)
\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)
Exercise \(\PageIndex{226}\)
\(1+\frac{5}{6}\)
- Answer
-
\(\frac{11}{6}\)
Exercise \(\PageIndex{227}\)
\(1-\frac{5}{9}\)
Use the Order of Operations to Simplify Complex Fractions
In the following exercises, simplify.
Exercise \(\PageIndex{228}\)
\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)
- Answer
-
\(\frac{1}{275}\)
Exercise \(\PageIndex{229}\)
\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)
Exercise \(\PageIndex{230}\)
\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)
- Answer
-
14
Exercise \(\PageIndex{231}\)
\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)
Evaluate Variable Expressions with Fractions
In the following exercises, evaluate.
Exercise \(\PageIndex{232}\)
\(x+\frac{1}{2}\) when
- \(x=-\frac{1}{8}\)
- \(x=-\frac{1}{2}\)
- Answer
-
- \(\frac{3}{8}\)
- \(0\)
Exercise \(\PageIndex{233}\)
\(x+\frac{2}{3}\) when
- \(x=-\frac{1}{6}\)
- \(x=-\frac{5}{3}\)
Exercise \(\PageIndex{234}\)
4\(p^{2} q\) when \(p=-\frac{1}{2}\) and \(q=\frac{5}{9}\)
- Answer
-
\(\frac{5}{9}\)
Exercise \(\PageIndex{235}\)
5\(m^{2} n\) when \(m=-\frac{2}{5}\) and \(n=\frac{1}{3}\)
Exercise \(\PageIndex{236}\)
\(\frac{u+v}{w}\) when
\(u=-4, v=-8, w=2\)
- Answer
-
-6
Exercise \(\PageIndex{237}\)
\(\frac{m+n}{p}\) when
\(m=-6, n=-2, p=4\)
Decimals
Name and Write Decimals
In the following exercises, write as a decimal.
Exercise \(\PageIndex{238}\)
Eight and three hundredths
- Answer
-
8.03
Exercise \(\PageIndex{239}\)
Nine and seven hundredths
Exercise \(\PageIndex{240}\)
One thousandth
- Answer
-
0.001
Exercise \(\PageIndex{241}\)
Nine thousandths
In the following exercises, name each decimal.
Exercise \(\PageIndex{242}\)
7.8
- Answer
-
seven and eight tenths
Exercise \(\PageIndex{243}\)
5.01
Exercise \(\PageIndex{244}\)
0.005
- Answer
-
five thousandths
Exercise \(\PageIndex{245}\)
0.381
Round Decimals
In the following exercises, round each number to the nearest
- hundredth
- tenth
- whole number.
Exercise \(\PageIndex{246}\)
5.7932
- Answer
-
- 5.79
- 5.8
- 6
Exercise \(\PageIndex{247}\)
3.6284
Exercise \(\PageIndex{248}\)
12.4768
- Answer
-
- 12.48
- 12.5
- 12
Exercise \(\PageIndex{249}\)
25.8449
Add and Subtract Decimals
In the following exercises, add or subtract.
Exercise \(\PageIndex{250}\)
18.37+9.36
- Answer
-
27.73
Exercise \(\PageIndex{251}\)
256.37−85.49
Exercise \(\PageIndex{252}\)
15.35−20.88
- Answer
-
−5.53
Exercise \(\PageIndex{253}\)
37.5+12.23
Exercise \(\PageIndex{254}\)
−4.2+(−9.3)
- Answer
-
−13.5
Exercise \(\PageIndex{255}\)
−8.6+(−8.6)
Exercise \(\PageIndex{256}\)
100−64.2
- Answer
-
35.8
Exercise \(\PageIndex{257}\)
100−65.83
Exercise \(\PageIndex{258}\)
2.51+40
- Answer
-
42.51
Exercise \(\PageIndex{259}\)
9.38+60
Multiply and Divide Decimals
In the following exercises, multiply.
Exercise \(\PageIndex{260}\)
(0.3)(0.4)
- Answer
-
0.12
Exercise \(\PageIndex{261}\)
(0.6)(0.7)
Exercise \(\PageIndex{262}\)
(8.52)(3.14)
- Answer
-
26.7528
Exercise \(\PageIndex{263}\)
(5.32)(4.86)
Exercise \(\PageIndex{264}\)
(0.09)(24.78)
- Answer
-
2.2302
Exercise \(\PageIndex{265}\)
(0.04)(36.89)
In the following exercises, divide.
Exercise \(\PageIndex{266}\)
\(0.15 \div 5\)
- Answer
-
0.03
Exercise \(\PageIndex{267}\)
\(0.27 \div 3\)
Exercise \(\PageIndex{268}\)
\(\$ 8.49 \div 12\)
- Answer
-
$0.71
Exercise \(\PageIndex{269}\)
\(\$ 16.99 \div 9\)
Exercise \(\PageIndex{270}\)
\(12 \div 0.08\)
- Answer
-
150
Exercise \(\PageIndex{271}\)
\(5 \div 0.04\)
Convert Decimals, Fractions, and Percents
In the following exercises, write each decimal as a fraction.
Exercise \(\PageIndex{272}\)
0.08
- Answer
-
\(\frac{2}{25}\)
Exercise \(\PageIndex{273}\)
0.17
Exercise \(\PageIndex{274}\)
0.425
- Answer
-
\(\frac{17}{40}\)
Exercise \(\PageIndex{275}\)
0.184
Exercise \(\PageIndex{276}\)
1.75
- Answer
-
\(\frac{7}{4}\)
Exercise \(\PageIndex{277}\)
0.035
In the following exercises, convert each fraction to a decimal.
Exercise \(\PageIndex{278}\)
\(\frac{2}{5}\)
- Answer
-
0.4
Exercise \(\PageIndex{279}\)
\(\frac{4}{5}\)
Exercise \(\PageIndex{280}\)
\(-\frac{3}{8}\)
- Answer
-
−0.375
Exercise \(\PageIndex{281}\)
\(-\frac{5}{8}\)
Exercise \(\PageIndex{282}\)
\(\frac{5}{9}\)
- Answer
-
\(0 . \overline{5}\)
Exercise \(\PageIndex{283}\)
\(\frac{2}{9}\)
Exercise \(\PageIndex{284}\)
\(\frac{1}{2}+6.5\)
- Answer
-
7
Exercise \(\PageIndex{285}\)
\(\frac{1}{4}+10.75\)
In the following exercises, convert each percent to a decimal.
Exercise \(\PageIndex{286}\)
5%
- Answer
-
0.05
Exercise \(\PageIndex{287}\)
9%
Exercise \(\PageIndex{288}\)
40%
- Answer
-
0.4
Exercise \(\PageIndex{289}\)
50%
Exercise \(\PageIndex{290}\)
115%
- Answer
-
1.15
Exercise \(\PageIndex{291}\)
125%
In the following exercises, convert each decimal to a percent.
Exercise \(\PageIndex{292}\)
0.18
- Answer
-
18%
Exercise \(\PageIndex{293}\)
0.15
Exercise \(\PageIndex{294}\)
0.009
- Answer
-
0.9%
Exercise \(\PageIndex{295}\)
0.008
Exercise \(\PageIndex{296}\)
1.5
- Answer
-
150%
Exercise \(\PageIndex{297}\)
2.2
The Real Numbers
Simplify Expressions with Square Roots
In the following exercises, simplify.
Exercise \(\PageIndex{298}\)
\(\sqrt{64}\)
- Answer
-
8
Exercise \(\PageIndex{299}\)
\(\sqrt{144}\)
Exercise \(\PageIndex{300}\)
\(-\sqrt{25}\)
- Answer
-
-5
Exercise \(\PageIndex{301}\)
\(-\sqrt{81}\)
Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers
In the following exercises, write as the ratio of two integers.
Exercise \(\PageIndex{302}\)
- 9
- 8.47
- Answer
-
- \(\frac{9}{1}\)
- \(\frac{847}{100}\)
Exercise \(\PageIndex{303}\)
- −15
- 3.591
In the following exercises, list the
- rational numbers,
- irrational numbers.
Exercise \(\PageIndex{304}\)
\(0.84,0.79132 \ldots, 1 . \overline{3}\)
- Answer
-
- \(0.84,1.3\)
- \(0.79132 \ldots\)
Exercise \(\PageIndex{305}\)
\(2.3 \overline{8}, 0.572,4.93814 \ldots\)
In the following exercises, identify whether each number is rational or irrational.
Exercise \(\PageIndex{306}\)
- \(\sqrt{121}\)
- \(\sqrt{48}\)
- Answer
-
- rational
- irrational
Exercise \(\PageIndex{307}\)
- \(\sqrt{56}\)
- \(\sqrt{16}\)
In the following exercises, identify whether each number is a real number or not a real number.
Exercise \(\PageIndex{308}\)
- \(\sqrt{-9}\)
- \(-\sqrt{169}\)
- Answer
-
- not a real number
- real number
Exercise \(\PageIndex{309}\)
- \(\sqrt{-64}\)
- \(-\sqrt{81}\)
In the following exercises, list the
- whole numbers,
- integers,
- rational numbers,
- irrational numbers,
- real numbers for each set of numbers.
Exercise \(\PageIndex{310}\)
\(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
- Answer
-
- \(0, \sqrt{16}\)
- \(-4,0, \sqrt{16}\)
- \(-4,0, \frac{5}{6}, \sqrt{16}\)
- \(\sqrt{18}, 5.2537 \ldots\)
- \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
Exercise \(\PageIndex{311}\)
\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)
Locate Fractions on the Number Line
In the following exercises, locate the numbers on a number line.
Exercise \(\PageIndex{312}\)
\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)
- Answer
-
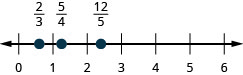
Exercise \(\PageIndex{313}\)
\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)
Exercise \(\PageIndex{314}\)
\(2 \frac{1}{3},-2 \frac{1}{3}\)
- Answer
-
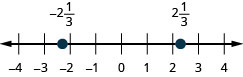
Exercise \(\PageIndex{315}\)
\(1 \frac{3}{5},-1 \frac{3}{5}\)
In the following exercises, order each of the following pairs of numbers, using < or >.
Exercise \(\PageIndex{316}\)
−1___\(-\frac{1}{8}\)
- Answer
-
<
Exercise \(\PageIndex{317}\)
\(-3 \frac{1}{4}\)___−4
Exercise \(\PageIndex{318}\)
\(-\frac{7}{9}\) ___ \(\frac{4}{9}\)
- Answer
-
>
Exercise \(\PageIndex{319}\)
\(-2\) ___ \(\frac{19}{8}\)
Locate Decimals on the Number Line
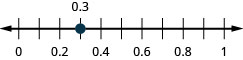
In the following exercises, locate on the number line.
Exercise \(\PageIndex{320}\)
0.3
- Answer
-
Exercise \(\PageIndex{321}\)
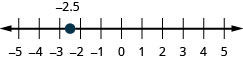
−0.2
Exercise \(\PageIndex{322}\)
−2.5
- Answer
-
Exercise \(\PageIndex{323}\)
2.7
In the following exercises, order each of the following pairs of numbers, using < or >.
Exercise \(\PageIndex{324}\)
0.9___0.6
- Answer
-
>
Exercise \(\PageIndex{325}\)
0.7___0.8
Exercise \(\PageIndex{326}\)
−0.6___−0.59
- Answer
-
>
Exercise \(\PageIndex{327}\)
−0.27___−0.3
Properties of Real Numbers
Use the Commutative and Associative Properties
In the following exercises, use the Associative Property to simplify.
Exercise \(\PageIndex{328}\)
−12(4m)
- Answer
-
−48m
Exercise \(\PageIndex{329}\)
30\(\left(\frac{5}{6} q\right)\)
Exercise \(\PageIndex{330}\)
(a+16)+31
- Answer
-
a+47
Exercise \(\PageIndex{331}\)
(c+0.2)+0.7
In the following exercises, simplify.
Exercise \(\PageIndex{332}\)
6y+37+(−6y)
- Answer
-
37
Exercise \(\PageIndex{333}\)
\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)
Exercise \(\PageIndex{334}\)
\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)
- Answer
-
\(\frac{35}{9}\)
Exercise \(\PageIndex{335}\)
\(-18 \cdot 15 \cdot \frac{2}{9}\)
Exercise \(\PageIndex{336}\)
\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)
- Answer
-
1\(\frac{7}{12}\)
Exercise \(\PageIndex{337}\)
(3.98d+0.75d)+1.25d
Exercise \(\PageIndex{338}\)
11x+8y+16x+15y
- Answer
-
27x+23y
Exercise \(\PageIndex{339}\)
52m+(−20n)+(−18m)+(−5n)
Use the Identity and Inverse Properties of Addition and Multiplication
In the following exercises, find the additive inverse of each number.
Exercise \(\PageIndex{340}\)
- \(\frac{1}{3}\)
- 5.1
- \(-14\)
- \(-\frac{8}{5}\)
- Answer
-
- \(-\frac{1}{3}\)
- \(-5.1\)
- -14
- \(-\frac{8}{5}\)
Exercise \(\PageIndex{341}\)
- \(-\frac{7}{8}\)
- \(-0.03\)
- 17
- \(\frac{12}{5}\)
In the following exercises, find the multiplicative inverse of each number.
Exercise \(\PageIndex{342}\)
- \(10\)
- \(-\frac{4}{9}\)
- 0.6
- Answer
-
- \(\frac{1}{10}\)
- \(-\frac{9}{4}\)
- \(\frac{5}{3}\)
Exercise \(\PageIndex{343}\)
- \(-\frac{9}{2}\)
- -7
- 2.1
Use the Properties of Zero
In the following exercises, simplify.
Exercise \(\PageIndex{344}\)
83\(\cdot 0\)
- Answer
-
0
Exercise \(\PageIndex{345}\)
\(\frac{0}{9}\)
Exercise \(\PageIndex{346}\)
\(\frac{5}{0}\)
- Answer
-
undefined
Exercise \(\PageIndex{347}\)
\(0 \div \frac{2}{3}\)
In the following exercises, simplify.
Exercise \(\PageIndex{348}\)
43+39+(−43)
- Answer
-
39
Exercise \(\PageIndex{349}\)
(n+6.75)+0.25
Exercise \(\PageIndex{350}\)
\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)
- Answer
-
57
Exercise \(\PageIndex{351}\)
\(\frac{1}{6} \cdot 17 \cdot 12\)
Exercise \(\PageIndex{352}\)
\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)
- Answer
-
8
Exercise \(\PageIndex{353}\)
\(9(6 x-11)+15\)
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the Distributive Property.
Exercise \(\PageIndex{354}\)
7(x+9)
- Answer
-
7x+63
Exercise \(\PageIndex{355}\)
9(u−4)
Exercise \(\PageIndex{356}\)
−3(6m−1)
- Answer
-
−18m+3
Exercise \(\PageIndex{357}\)
−8(−7a−12)
Exercise \(\PageIndex{358}\)
\(\frac{1}{3}(15 n-6)\)
- Answer
-
5n−2
Exercise \(\PageIndex{359}\)
\((y+10) \cdot p\)
Exercise \(\PageIndex{360}\)
(a−4)−(6a+9)
- Answer
-
−5a−13
Exercise \(\PageIndex{361}\)
4(x+3)−8(x−7)
Systems of Measurement
1.1 Define U.S. Units of Measurement and Convert from One Unit to Another
In the following exercises, convert the units. Round to the nearest tenth.
Exercise \(\PageIndex{362}\)
A floral arbor is 7 feet tall. Convert the height to inches.
- Answer
-
84 inches
Exercise \(\PageIndex{363}\)
A picture frame is 42 inches wide. Convert the width to feet.
Exercise \(\PageIndex{364}\)
Kelly is 5 feet 4 inches tall. Convert her height to inches.
- Answer
-
64 inches
Exercise \(\PageIndex{365}\)
A playground is 45 feet wide. Convert the width to yards.
Exercise \(\PageIndex{366}\)
The height of Mount Shasta is 14,179 feet. Convert the height to miles.
- Answer
-
2.7 miles
Exercise \(\PageIndex{367}\)
Shamu weights 4.5 tons. Convert the weight to pounds.
Exercise \(\PageIndex{368}\)
The play lasted \(1\frac{3}{4}\) hours. Convert the time to minutes.
- Answer
-
105 minutes
Exercise \(\PageIndex{369}\)
How many tablespoons are in a quart?
Exercise \(\PageIndex{370}\)
Naomi’s baby weighed 5 pounds 14 ounces at birth. Convert the weight to ounces.
- Answer
-
94 ounces
Exercise \(\PageIndex{371}\)
Trinh needs 30 cups of paint for her class art project. Convert the volume to gallons.
Use Mixed Units of Measurement in the U.S. System.
In the following exercises, solve.
Exercise \(\PageIndex{372}\)
John caught 4 lobsters. The weights of the lobsters were 1 pound 9 ounces, 1 pound 12 ounces, 4 pounds 2 ounces, and 2 pounds 15 ounces. What was the total weight of the lobsters?
- Answer
-
10 lbs. 6 oz.
Exercise \(\PageIndex{373}\)
Every day last week Pedro recorded the number of minutes he spent reading. The number of minutes were 50, 25, 83, 45, 32, 60, 135. How many hours did Pedro spend reading?
Exercise \(\PageIndex{374}\)
Fouad is 6 feet 2 inches tall. If he stands on a rung of a ladder 8 feet 10 inches high, how high off the ground is the top of Fouad’s head?
- Answer
-
15 feet
Exercise \(\PageIndex{375}\)
Dalila wants to make throw pillow covers. Each cover takes 30 inches of fabric. How many yards of fabric does she need for 4 covers?
Make Unit Conversions in the Metric System
In the following exercises, convert the units.
Exercise \(\PageIndex{376}\)
Donna is 1.7 meters tall. Convert her height to centimeters.
- Answer
-
170 centimeters
Exercise \(\PageIndex{377}\)
Mount Everest is 8,850 meters tall. Convert the height to kilometers.
Exercise \(\PageIndex{378}\)
One cup of yogurt contains 488 milligrams of calcium. Convert this to grams.
- Answer
-
0.488 grams
Exercise \(\PageIndex{379}\)
One cup of yogurt contains 13 grams of protein. Convert this to milligrams.
Exercise \(\PageIndex{380}\)
Sergio weighed 2.9 kilograms at birth. Convert this to grams.
- Answer
-
2,900 grams
Exercise \(\PageIndex{381}\)
A bottle of water contained 650 milliliters. Convert this to liters.
Use Mixed Units of Measurement in the Metric System
In the following exerices, solve.
Exercise \(\PageIndex{382}\)
Minh is 2 meters tall. His daughter is 88 centimeters tall. How much taller is Minh than his daughter?
- Answer
-
1.12 meter
Exercise \(\PageIndex{383}\)
Selma had a 1 liter bottle of water. If she drank 145 milliliters, how much water was left in the bottle?
Exercise \(\PageIndex{384}\)
One serving of cranberry juice contains 30 grams of sugar. How many kilograms of sugar are in 30 servings of cranberry juice?
- Answer
-
0.9 kilograms
Exercise \(\PageIndex{385}\)
One ounce of tofu provided 2 grams of protein. How many milligrams of protein are provided by 5 ounces of tofu?
Convert between the U.S. and the Metric Systems of Measurement
In the following exercises, make the unit conversions. Round to the nearest tenth.
Exercise \(\PageIndex{386}\)
Majid is 69 inches tall. Convert his height to centimeters.
- Answer
-
175.3 centimeters
Exercise \(\PageIndex{387}\)
A college basketball court is 84 feet long. Convert this length to meters.
Exercise \(\PageIndex{388}\)
Caroline walked 2.5 kilometers. Convert this length to miles.
- Answer
-
1.6 miles
Exercise \(\PageIndex{389}\)
Lucas weighs 78 kilograms. Convert his weight to pounds.
Exercise \(\PageIndex{390}\)
Steve’s car holds 55 liters of gas. Convert this to gallons.
- Answer
-
14.6 gallons
Exercise \(\PageIndex{391}\)
A box of books weighs 25 pounds. Convert the weight to kilograms.
Convert between Fahrenheit and Celsius Temperatures
In the following exercises, convert the Fahrenheit temperatures to degrees Celsius. Round to the nearest tenth.
Exercise \(\PageIndex{392}\)
95° Fahrenheit
- Answer
-
35° C
Exercise \(\PageIndex{393}\)
23° Fahrenheit
Exercise \(\PageIndex{394}\)
20° Fahrenheit
- Answer
-
–6.7° C
Exercise \(\PageIndex{395}\)
64° Fahrenheit
In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.
Exercise \(\PageIndex{396}\)
30° Celsius
- Answer
-
86° F
Exercise \(\PageIndex{397}\)
–5° Celsius
Exercise \(\PageIndex{398}\)
–12° Celsius
- Answer
-
10.4° F
Exercise \(\PageIndex{399}\)
24° Celsius
Chapter Practice Test
Exercise \(\PageIndex{1}\)
Write as a whole number using digits: two hundred five thousand, six hundred seventeen.
- Answer
-
205,617
Exercise \(\PageIndex{2}\)
Find the prime factorization of 504.
Exercise \(\PageIndex{3}\)
Find the Least Common Multiple of 18 and 24.
- Answer
-
72
Exercise \(\PageIndex{4}\)
Combine like terms: 5n+8+2n−1.
In the following exercises, evaluate.
Exercise \(\PageIndex{5}\)
\(-|x|\) when \(x=-2\)
- Answer
-
−2
Exercise \(\PageIndex{6}\)
11−a when a=−3
Exercise \(\PageIndex{7}\)
Translate to an algebraic expression and simplify: twenty less than negative 7.
- Answer
-
−7−20;−27
Exercise \(\PageIndex{8}\)
Monique has a balance of −$18 in her checking account. She deposits $152 to the account. What is the new balance?
Exercise \(\PageIndex{9}\)
Round 677.1348 to the nearest hundredth.
- Answer
-
677.13
Exercise \(\PageIndex{10}\)
Convert \(\frac{4}{5}\) to a decimal.
Exercise \(\PageIndex{11}\)
Convert 1.85 to a percent.
- Answer
-
185%
Exercise \(\PageIndex{12}\)
Locate \(\frac{2}{3},-1.5,\) and \(\frac{9}{4}\) on a number line.
In the following exercises, simplify each expression.
Exercise \(\PageIndex{13}\)
\(4+10(3+9)-5^{2}\)
- Answer
-
99
Exercise \(\PageIndex{14}\)
−85+42
Exercise \(\PageIndex{15}\)
−19−25
- Answer
-
−44
Exercise \(\PageIndex{16}\)
\((-2)^{4}\)
Exercise \(\PageIndex{17}\)
\(-5(-9) \div 15\)
- Answer
-
3
Exercise \(\PageIndex{18}\)
\(\frac{3}{8} \cdot \frac{11}{12}\)
Exercise \(\PageIndex{19}\)
\(\frac{4}{5} \div \frac{9}{20}\)
- Answer
-
\(\frac{16}{9}\)
Exercise \(\PageIndex{20}\)
\(\frac{12+3 \cdot 5}{15-6}\)
Exercise \(\PageIndex{21}\)
\(\frac{m}{7}+\frac{10}{7}\)
- Answer
-
\(\frac{m+10}{7}\)
Exercise \(\PageIndex{22}\)
\(\frac{7}{12}-\frac{3}{8}\)
Exercise \(\PageIndex{23}\)
\(-5.8+(-4.7)\)
- Answer
-
−10.5
Exercise \(\PageIndex{24}\)
100−64.25
Exercise \(\PageIndex{25}\)
(0.07)(31.95)
- Answer
-
2.2365
Exercise \(\PageIndex{26}\)
\(9 \div 0.05\)
Exercise \(\PageIndex{27}\)
\(-14\left(\frac{5}{7} p\right)\)
- Answer
-
−10p
Exercise \(\PageIndex{28}\)
(u+8)−9
Exercise \(\PageIndex{29}\)
6x+(−4y)+9x+8y
- Answer
-
15x+4y
Exercise \(\PageIndex{30}\)
\(\frac{0}{23}\)
Exercise \(\PageIndex{31}\)
\(\frac{75}{0}\)
- Answer
-
undefined
Exercise \(\PageIndex{32}\)
−2(13q−5)
Exercise \(\PageIndex{33}\)
A movie lasted 1\(\frac{2}{3}\) hours. How many minutes did it last? ( 1 hour \(=60\) minutes)
- Answer
-
100 minutes
Exercise \(\PageIndex{34}\)
Mike’s SUV is 5 feet 11 inches tall. He wants to put a rooftop cargo bag on the the SUV. The cargo bag is 1 foot 6 inches tall. What will the total height be of the SUV with the cargo bag on the roof? (1 foot = 12 inches)
Exercise \(\PageIndex{35}\)
Jennifer ran 2.8 miles. Convert this length to kilometers. (1 mile = 1.61 kilometers)
- Answer
-
4.508 km


