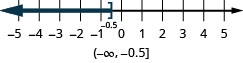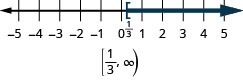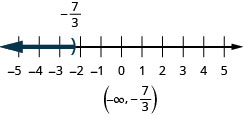2.7E: Exercises
- Last updated
- Save as PDF
- Page ID
- 30373
Practice Makes Perfect
Graph Inequalities on the Number Line
In the following exercises, graph each inequality on the number line
Exercise \(\PageIndex{1}\)
- \(x\leq 2\)
- x>−1
- x<0
Exercise \(\PageIndex{2}\)
- x>1
- x<−2
- \(x\geq −3\)
- Answer
-
Exercise \(\PageIndex{3}\)
- \(x\geq −3\)
- x<4
- \(x\leq −2\)
Exercise \(\PageIndex{4}\)
- \(x\leq 0\)
- x>−4
- \(x\geq −1\)
- Answer
-
In the following exercises, graph each inequality on the number line and write in interval notation.
Exercise \(\PageIndex{5}\)
- x<−2
- \(x\geq −3.5\)
- \( x\leq \frac{2}{3}\)
Exercise \(\PageIndex{6}\)
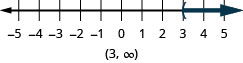
- \(x>3\)
- \(x \leq-0.5\)
- \(x \geq \frac{1}{3}\)
- Answer
-
Exercise \(\PageIndex{7}\)
- \(x \geq-4\)
- x<2.5
- \(x>-\frac{3}{2}\)
Exercise \(\PageIndex{8}\)
- \(x\leq 5\)
- \(x\geq −1.5x\)
- x<−73
- Answer
-
Solve Inequalities using the Subtraction and Addition Properties of Inequality
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \(\PageIndex{9}\)
\(n-11<33\)
Exercise \(\PageIndex{10}\)
\(m-45 \leq 62\)
- Answer
-
Exercise \(\PageIndex{11}\)
\(u+25>21\)
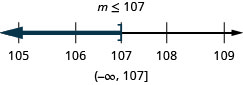
Exercise \(\PageIndex{12}\)
\(v+12>3\)
- Answer
-
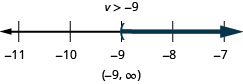
Exercise \(\PageIndex{13}\)
\(a+\frac{3}{4} \geq \frac{7}{10}\)
Exercise \(\PageIndex{14}\)
\(b+\frac{7}{8} \geq \frac{1}{6}\)
- Answer
-
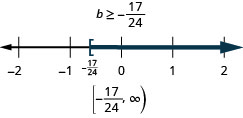
Exercise \(\PageIndex{15}\)
\(f-\frac{13}{20}<-\frac{5}{12}\)
Exercise \(\PageIndex{16}\)
\(g-\frac{11}{12}<-\frac{5}{18}\)
- Answer
-
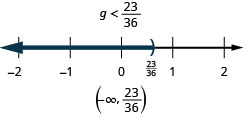
Solve Inequalities using the Division and Multiplication Properties of Inequality
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \(\PageIndex{17}\)
\(8 x>72\)
Exercise \(\PageIndex{18}\)
\(6 y<48\)
- Answer
-
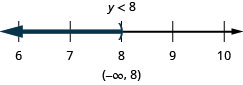
Exercise \(\PageIndex{19}\)
\(7 r \leq 56\)
Exercise \(\PageIndex{20}\)
\(9 s \geq 81\)
- Answer
-
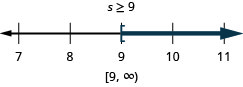
Exercise \(\PageIndex{21}\)
\(-5 u \geq 65\)
Exercise \(\PageIndex{22}\)
\(-8 v \leq 96\)
- Answer
-
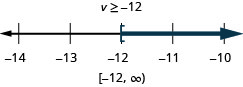
Exercise \(\PageIndex{23}\)
\(-9 c<126\)
Exercise \(\PageIndex{24}\)
\(-7 d>105\)
- Answer
-
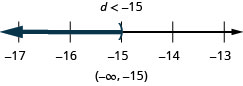
Exercise \(\PageIndex{25}\)
\(20>\frac{2}{5} h\)
Exercise \(\PageIndex{26}\)
\(40<\frac{5}{8} k\)
- Answer
-
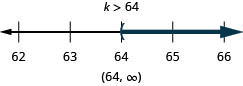
Exercise \(\PageIndex{27}\)
\(\frac{7}{6} j \geq 42\)
Exercise \(\PageIndex{28}\)
\(\frac{9}{4} g \leq 36\)
- Answer
-
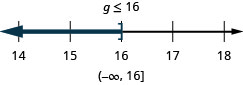
Exercise \(\PageIndex{29}\)
\(\frac{a}{-3} \leq 9\)
Exercise \(\PageIndex{30}\)
\(\frac{b}{-10} \geq 30\)
- Answer
-
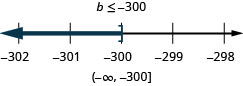
Exercise \(\PageIndex{31}\)
\(-25<\frac{p}{-5}\)
Exercise \(\PageIndex{32}\)
\(-18>\frac{q}{-6}\)
- Answer
-
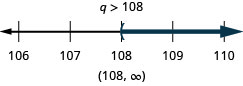
Exercise \(\PageIndex{33}\)
\(9 t \geq-27\)
Exercise \(\PageIndex{34}\)
\(7 s<-28\)
- Answer
-
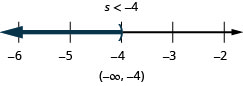
Exercise \(\PageIndex{35}\)
\(\frac{2}{3} y>-36\)
Exercise \(\PageIndex{36}\)
\(\frac{3}{5} x \leq-45\)
- Answer
-
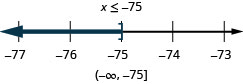
Solve Inequalities That Require Simplification
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \(\PageIndex{37}\)
\(4 v \geq 9 v-40\)
Exercise \(\PageIndex{38}\)
\(5 u \leq 8 u-21\)
- Answer
-
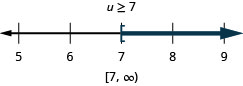
Exercise \(\PageIndex{39}\)
\(13 q<7 q-29\)
Exercise \(\PageIndex{40}\)
\(9 p>14 p-18\)
- Answer
-
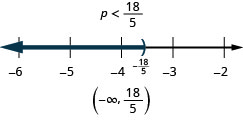
Exercise \(\PageIndex{41}\)
\(12 x+3(x+7)>10 x-24\)
Exercise \(\PageIndex{42}\)
\(9 y+5(y+3)<4 y-35\)
- Answer
-
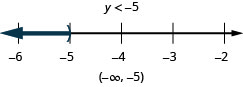
Exercise \(\PageIndex{43}\)
\(6 h-4(h-1) \leq 7 h-11\)
Exercise \(\PageIndex{44}\)
\(4 k-(k-2) \geq 7 k-26\)
- Answer
-
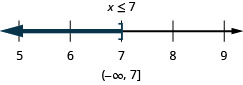
Exercise \(\PageIndex{45}\)
\(8 m-2(14-m) \geq 7(m-4)+3 m\)
Exercise \(\PageIndex{46}\)
\(6 n-12(3-n) \leq 9(n-4)+9 n\)
- Answer
-
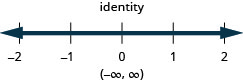
Exercise \(\PageIndex{47}\)
\(\frac{3}{4} b-\frac{1}{3} b<\frac{5}{12} b-\frac{1}{2}\)
Exercise \(\PageIndex{48}\)
\(9 u+5(2 u-5) \geq 12(u-1)+7 u\)
- Answer
-
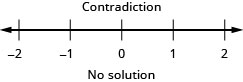
Exercise \(\PageIndex{49}\)
\(\frac{2}{3} g-\frac{1}{2}(g-14) \leq \frac{1}{6}(g+42)\)
Exercise \(\PageIndex{50}\)
\(\frac{5}{6} a-\frac{1}{4} a>\frac{7}{12} a+\frac{2}{3}\)
- Answer
-
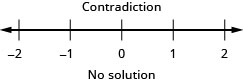
Exercise \(\PageIndex{51}\)
\(\frac{4}{5} h-\frac{2}{3}(h-9) \geq \frac{1}{15}(2 h+90)\)
Exercise \(\PageIndex{52}\)
\(12 v+3(4 v-1) \leq 19(v-2)+5 v\)
- Answer
-
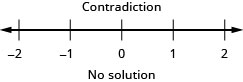
Mixed practice
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \(\PageIndex{53}\)
\(15 k \leq-40\)
Exercise \(\PageIndex{54}\)
\(35 k \geq-77\)
- Answer
-
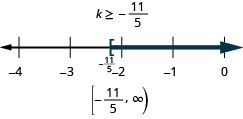
Exercise \(\PageIndex{55}\)
\(23 p-2(6-5 p)>3(11 p-4)\)
Exercise \(\PageIndex{56}\)
\(18 q-4(10-3 q)<5(6 q-8)\)
- Answer
-
Exercise \(\PageIndex{57}\)
\(-\frac{9}{4} x \geq-\frac{5}{12}\)
Exercise \(\PageIndex{58}\)
\(-\frac{21}{8} y \leq-\frac{15}{28}\)
- Answer
-
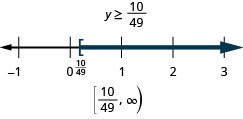
Exercise \(\PageIndex{59}\)
\(c+34<-99\)
Exercise \(\PageIndex{60}\)
\(d+29>-61\)
- Answer
-
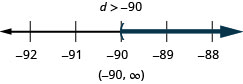
Exercise \(\PageIndex{61}\)
\(\frac{m}{18} \geq-4\)
Exercise \(\PageIndex{62}\)
\(\frac{n}{13} \leq-6\)
- Answer
-
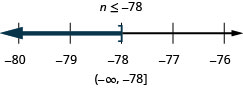
Translate to an Inequality and Solve
In the following exercises, translate and solve .Then write the solution in interval notation and graph on the number line.
Exercise \(\PageIndex{63}\)
Fourteen times d is greater than 56.
Exercise \(\PageIndex{64}\)
Ninety times c is less than 450.
- Answer
-
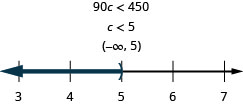
Exercise \(\PageIndex{65}\)
Eight times \(z\) is smaller than \(-40\)
Exercise \(\PageIndex{66}\)
Ten times \(y\) is at most \(-110\)
- Answer
-
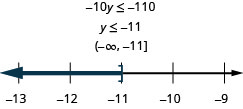
Exercise \(\PageIndex{67}\)
Three more than \(h\) is no less than 25
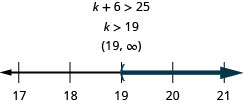
Exercise \(\PageIndex{68}\)
Six more than \(k\) exceeds 25
- Answer
-
Exercise \(\PageIndex{69}\)
Ten less than \(w\) is at least \(39 .\)
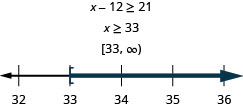
Exercise \(\PageIndex{70}\)
Twelve less than \(x\) is no less than 21
- Answer
-
Exercise \(\PageIndex{71}\)
Negative five times \(r\) is no more than \(95 .\)
Exercise \(\PageIndex{72}\)
Negative two times s is lower than 56
- Answer
-
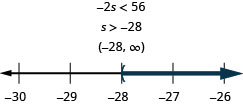
Exercise \(\PageIndex{73}\)
Nineteen less than \(b\) is at most \(-22\)
Exercise \(\PageIndex{74}\)
Fifteen less than a is at least \(-7\)
- Answer
-
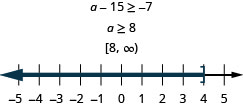
Everyday Math
Exercise \(\PageIndex{75}\)
Safety A child’s height, h, must be at least 57 inches for the child to safely ride in the front seat of a car. Write this as an inequality.
Exercise \(\PageIndex{76}\)
Fighter pilots The maximum height, h, of a fighter pilot is 77 inches. Write this as an inequality.
- Answer
-
\(h \leq 77\)
Exercise \(\PageIndex{77}\)
Elevators The total weight, w, of an elevator’s passengers can be no more than 1,200 pounds. Write this as an inequality.
Exercise \(\PageIndex{78}\)
Shopping The number of items, n, a shopper can have in the express check-out lane is at most 8. Write this as an inequality.
- Answer
-
\(n \leq 8\)
Writing Exercises
Exercise \(\PageIndex{79}\)
Give an example from your life using the phrase ‘at least’.
Exercise \(\PageIndex{80}\)
Give an example from your life using the phrase ‘at most’.
- Answer
-
Answers will vary.
Exercise \(\PageIndex{81}\)
Explain why it is necessary to reverse the inequality when solving \(-5 x>10\)
Exercise \(\PageIndex{82}\)
Explain why it is necessary to reverse the inequality when solving \(\frac{n}{-3}<12\)
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?