3.2E: Exercises
- Page ID
- 30379
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Translate and Solve Basic Percent Equations
In the following exercises, translate and solve.
What number is 45% of 120?
- Answer
-
54
What number is 65% of 100?
What number is 24% of 112?
- Answer
-
26.88
What number is 36% of 124?
250% of 65 is what number?
- Answer
-
162.5
150% of 90 is what number?
800% of 2250 is what number?
- Answer
-
18,000
600% of 1740 is what number?
28 is 25% of what number?
- Answer
-
112
36 is 25% of what number?
81 is 75% of what number?
- Answer
-
108
93 is 75% of what number?
8.2% of what number is $2.87?
- Answer
-
$35
6.4% of what number is $2.88?
11.5% of what number is $108.10?
- Answer
-
$940
12.3% of what number is $92.25?
What percent of 260 is 78?
- Answer
-
30%
What percent of 215 is 86?
What percent of 1500 is 540?
- Answer
-
36%
What percent of 1800 is 846?
30 is what percent of 20?
- Answer
-
150%
50 is what percent of 40?
840 is what percent of 480?
- Answer
-
175%
790 is what percent of 395?
Solve Percent Applications
In the following exercises, solve.
Geneva treated her parents to dinner at their favorite restaurant. The bill was $74.25. Geneva wants to leave 16% of the total bill as a tip. How much should the tip be?
- Answer
-
$11.88
When Hiro and his co-workers had lunch at a restaurant near their work, the bill was $90.50. They want to leave 18% of the total bill as a tip. How much should the tip be?
Trong has 12% of each paycheck automatically deposited to his savings account. His last paycheck was $2165. How much money was deposited to Trong’s savings account?
- Answer
-
$259.80
Cherise deposits 8% of each paycheck into her retirement account. Her last paycheck was $1,485. How much did Cherise deposit into her retirement account?
One serving of oatmeal has eight grams of fiber, which is 33% of the recommended daily amount. What is the total recommended daily amount of fiber?
- Answer
-
24.2 g
One serving of trail mix has 67 grams of carbohydrates, which is 22% of the recommended daily amount. What is the total recommended daily amount of carbohydrates?
A bacon cheeseburger at a popular fast food restaurant contains 2070 milligrams (mg) of sodium, which is 86% of the recommended daily amount. What is the total recommended daily amount of sodium?
- Answer
-
2407 mg
A grilled chicken salad at a popular fast food restaurant contains 650 milligrams (mg) of sodium, which is 27% of the recommended daily amount. What is the total recommended daily amount of sodium?
After 3 months on a diet, Lisa had lost 12% of her original weight. She lost 21 pounds. What was Lisa’s original weight?
- Answer
-
175 lb.
Tricia got a 6% raise on her weekly salary. The raise was $30 per week. What was her original salary?
Yuki bought a dress on sale for $72. The sale price was 60% of the original price. What was the original price of the dress?
- Answer
-
$120
Kim bought a pair of shoes on sale for $40.50. The sale price was 45% of the original price. What was the original price of the shoes?
Tim left a $9 tip for a $50 restaurant bill. What percent tip did he leave?
- Answer
-
18%
Rashid left a $15 tip for a $75 restaurant bill. What percent tip did he leave?
The nutrition fact sheet at a fast food restaurant says the fish sandwich has 380 calories, and 171 calories are from fat. What percent of the total calories is from fat?
- Answer
-
45%
The nutrition fact sheet at a fast food restaurant says a small portion of chicken nuggets has 190 calories, and 114 calories are from fat. What percent of the total calories is from fat?
Emma gets paid $3,000 per month. She pays $750 a month for rent. What percent of her monthly pay goes to rent?
- Answer
-
25%
Dimple gets paid $3,200 per month. She pays $960 a month for rent. What percent of her monthly pay goes to rent?
Find Percent Increase and Percent Decrease
In the following exercises, solve.
Tamanika got a raise in her hourly pay, from $15.50 to $17.36. Find the percent increase.
- Answer
-
12%
Ayodele got a raise in her hourly pay, from $24.50 to $25.48. Find the percent increase.
Annual student fees at the University of California rose from about $4,000 in 2000 to about $12,000 in 2010. Find the percent increase.
- Answer
-
200%
The price of a share of one stock rose from $12.50 to $50. Find the percent increase.
According to Time magazine annual global seafood consumption rose from 22 pounds per person in the 1960s to 38 pounds per person in 2011. Find the percent increase. (Round to the nearest tenth of a percent.)
- Answer
-
72.7%
In one month, the median home price in the Northeast rose from $225,400 to $241,500. Find the percent increase. (Round to the nearest tenth of a percent.)
A grocery store reduced the price of a loaf of bread from $2.80 to $2.73. Find the percent decrease.
- Answer
-
2.5%
The price of a share of one stock fell from $8.75 to $8.54. Find the percent decrease.
Hernando’s salary was $49,500 last year. This year his salary was cut to $44,055. Find the percent decrease.
- Answer
-
11%
In 10 years, the population of Detroit fell from 950,000 to about 712,500. Find the percent decrease.
In 1 month, the median home price in the West fell from $203,400 to $192,300. Find the percent decrease. (Round to the nearest tenth of a percent.)
- Answer
-
5.5%
Sales of video games and consoles fell from $1,150 million to $1,030 million in 1 year. Find the percent decrease. (Round to the nearest tenth of a percent.)
Solve Simple Interest Applications
In the following exercises, solve.
Casey deposited $1,450 in a bank account with interest rate 4%. How much interest was earned in two years?
- Answer
-
$116
Terrence deposited $5,720 in a bank account with interest rate 6%. How much interest was earned in 4 years?
Robin deposited $31,000 in a bank account with interest rate 5.2%. How much interest was earned in 3 years?
- Answer
-
$4,836
Carleen deposited $16,400 in a bank account with interest rate 3.9%. How much interest was earned in 8 years?
Hilaria borrowed $8,000 from her grandfather to pay for college. Five years later, she paid him back the $8,000, plus $1,200 interest. What was the rate of interest?
- Answer
-
3%
Kenneth loaned his niece $1,200 to buy a computer. Two years later, she paid him back the $1,200, plus $96 interest. What was the rate of interest?
Lebron loaned his daughter $20,000 to help her buy a condominium. When she sold the condominium four years later, she paid him the $20,000, plus $3,000 interest. What was the rate of interest?
- Answer
-
3.75%
Pablo borrowed $50,000 to start a business. Three years later, he repaid the $50,000, plus $9,375 interest. What was the rate of interest?
In 10 years, a bank account that paid 5.25% earned $18,375 interest. What was the principal of the account?
- Answer
-
$35,000
In 25 years, a bond that paid 4.75% earned $2,375 interest. What was the principal of the bond?
Joshua’s computer loan statement said he would pay $1,244.34 in interest for a 3-year loan at 12.4%. How much did Joshua borrow to buy the computer?
- Answer
-
$3,345
Margaret’s car loan statement said she would pay $7,683.20 in interest for a 5-year loan at 9.8%. How much did Margaret borrow to buy the car?
Solve Applications with Discount or Mark-up
In the following exercises, find the sale price.
Perla bought a cell phone that was on sale for $50 off. The original price of the cell phone was $189.
- Answer
-
$139
Sophie saw a dress she liked on sale for $15 off. The original price of the dress was $96.
Rick wants to buy a tool set with original price $165. Next week the tool set will be on sale for $40 off.
- Answer
-
$125
Angelo’s store is having a sale on televisions. One television, with original price $859, is selling for $125 off.
In the following exercises, find
- the amount of discount and
- the sale price.
Janelle bought a beach chair on sale at 60% off. The original price was $44.95.
- Answer
-
- $26.97
- $17.98
Errol bought a skateboard helmet on sale at 40% off. The original price was $49.95.
Kathy wants to buy a camera that lists for $389. The camera is on sale with a 33% discount.
- Answer
-
- $128.37
- $260.63
Colleen bought a suit that was discounted 25% from an original price of $245.
Erys bought a treadmill on sale at 35% off. The original price was $949.95 (round to the nearest cent.)
- Answer
-
- $332.48
- $617.47
Jay bought a guitar on sale at 45% off. The original price was $514.75 (round to the nearest cent.)
In the following exercises, find
- the amount of discount and
- the discount rate. (Round to the nearest tenth of a percent if needed.)
Larry and Donna bought a sofa at the sale price of $1,344. The original price of the sofa was $1,920.
- Answer
-
- $576
- 30%
Hiroshi bought a lawnmower at the sale price of $240. The original price of the lawnmower is $300.
Patty bought a baby stroller on sale for $301.75. The original price of the stroller was $355.
- Answer
-
- $53.25
- 15%
Bill found a book he wanted on sale for $20.80. The original price of the book was $32.
Nikki bought a patio set on sale for $480. The original price was $850. To the nearest tenth of a percent, what was the rate of discount?
- Answer
-
- $370
- 43.5%
Stella bought a dinette set on sale for $725. The original price was $1,299. To the nearest tenth of a percent, what was the rate of discount?
In the following exercises, find ⓐ the amount of the mark-up and ⓑ the list price.
Daria bought a bracelet at original cost $16 to sell in her handicraft store. She marked the price up 45%.
- Answer
-
- $7.20
- $23.20
Regina bought a handmade quilt at original cost $120 to sell in her quilt store. She marked the price up 55%.
Tom paid $0.60 a pound for tomatoes to sell at his produce store. He added a 33% mark-up.
- Answer
-
- $0.20
- $0.80
Flora paid her supplier $0.74 a stem for roses to sell at her flower shop. She added an 85% mark-up.
Alan bought a used bicycle for $115. After re-conditioning it, he added 225% mark-up and then advertised it for sale.
- Answer
-
- $258.75
- $373.75
Michael bought a classic car for $8,500. He restored it, then added 150% mark-up before advertising it for sale.
Everyday Math
Leaving a Tip At the campus coffee cart, a medium coffee costs $1.65. MaryAnne brings $2.00 with her when she buys a cup of coffee and leaves the change as a tip. What percent tip does she leave?
- Answer
-
21.2%
Splitting a Bill Four friends went out to lunch and the bill came to $53.75. They decided to add enough tip to make a total of $64, so that they could easily split the bill evenly among themselves. What percent tip did they leave?
Writing Exercises
Without solving the problem “44 is 80% of what number” think about what the solution might be. Should it be a number that is greater than 44 or less than 44? Explain your reasoning.
- Answer
-
The number should be greater than 44. Since 80% equals 0.8 in decimal form, 0.8 is less than one, and we must multiply the number by 0.8 to get 44, the number must be greater than 44.
Without solving the problem “What is 20% of 300?” think about what the solution might be. Should it be a number that is greater than 300 or less than 300? Explain your reasoning.
After returning from vacation, Alex said he should have packed 50% fewer shorts and 200% more shirts. Explain what Alex meant.
- Answer
-
He meant that he should have packed half the shorts and twice the shirts.
Because of road construction in one city, commuters were advised to plan that their Monday morning commute would take 150% of their usual commuting time. Explain what this means.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
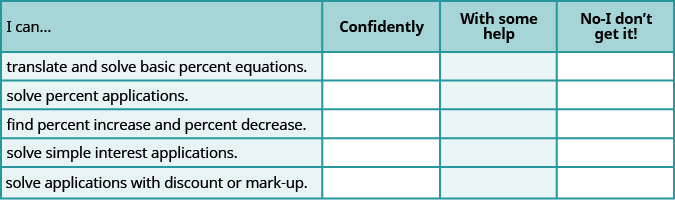
ⓑ After reviewing this checklist, what will you do to become confident for all goals?