4.1E: Exercises
- Last updated
- Save as PDF
- Page ID
- 30391
Practice Makes Perfect
Plot Points in a Rectangular Coordinate System
In the following exercises, plot each point in a rectangular coordinate system and identify the quadrant in which the point is located.
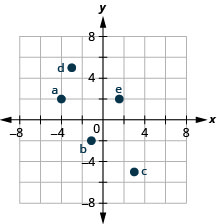
Exercise \(\PageIndex{1}\)
- (−4,2)
- (−1,−2)
- (3,−5)
- (−3,5)
- \((\frac{5}{3},2)\)
- Answer
-
Exercise \(\PageIndex{2}\)
- (−2,−3)
- (3,−3)
- (−4,1)
- (4,−1)
- \((\frac{3}{2},1)\)
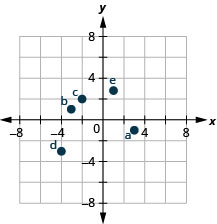
Exercise \(\PageIndex{3}\)
- (3,−1)
- (−3,1)
- (−2,2)
- (−4,−3)
- \(\left(1, \frac{14}{5}\right)\)
- Answer
-
Exercise \(\PageIndex{4}\)
- (−1,1)
- (−2,−1)
- (2,1)
- (1,−4)
- \(\left(3, \frac{7}{2}\right)\)
In the following exercises, plot each point in a rectangular coordinate system.
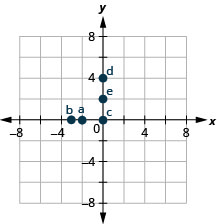
Exercise \(\PageIndex{5}\)
- (−2,0)
- (−3,0)
- (0,0)
- (0,4)
- (0,2)
- Answer
-
Exercise \(\PageIndex{6}\)
- (0,1)
- (0,−4)
- (−1,0)
- (0,0)
- (5,0)
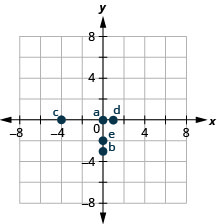
Exercise \(\PageIndex{7}\)
- (0,0)
- (0,−3)
- (−4,0)
- (1,0)
- (0,−2)
- Answer
-
Exercise \(\PageIndex{8}\)
- (−3,0)
- (0,5)
- (0,−2)
- (2,0)
- (0,0)
In the following exercises, name the ordered pair of each point shown in the rectangular coordinate system.
Exercise \(\PageIndex{9}\)
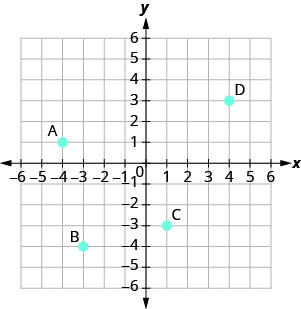
- Answer
-
\(A :(-4,1) \quad B :(-3,-4) \quad C :(1,-3) \quad D :(4,3)\)
Exercise \(\PageIndex{10}\)
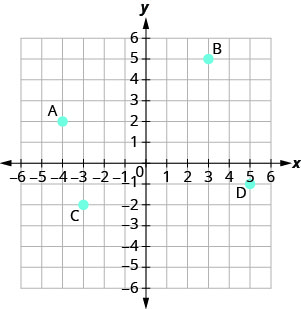
Exercise \(\PageIndex{11}\)
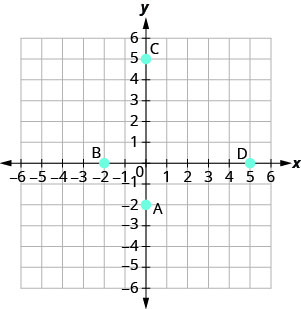
- Answer
-
\(A :(0,-2) \quad B :(-2,0) \quad C :(0,5) \quad D :(5,0)\)
Exercise \(\PageIndex{12}\)
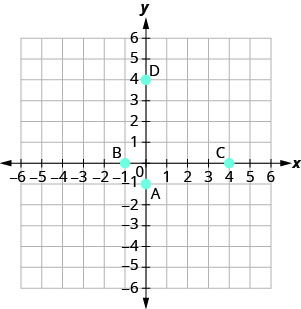
Verify Solutions to an Equation in Two Variables
In the following exercises, which ordered pairs are solutions to the given equations?
Exercise \(\PageIndex{13}\)
2x+y=6
- (1,4)
- (3,0)
- (2,3)
- Answer
-
1, 2
Exercise \(\PageIndex{14}\)
- x+3y=9
- (0,3)
- (6,1)
- (−3,−3)
Exercise \(\PageIndex{15}\)
4x−2y=8
- (3,2)
- (1,4)
- (0,−4)
- Answer
-
1, 3
Exercise \(\PageIndex{16}\)
3x−2y=12
- (4,0)
- (2,−3)
- (1,6)
Exercise \(\PageIndex{17}\)
y=4x+3
- (4,3)
- (−1,−1)
- \(\left(\frac{1}{2}, 5\right)\)
- Answer
-
2, 3
Exercise \(\PageIndex{18}\)
y=2x−5
- (0,−5)
- (2,1)
- \(\left(\frac{1}{2},-4\right)\)
Exercise \(\PageIndex{19}\)
\(y=\frac{1}{2}x−1\)
- (2,0)
- (−6,−4)
- (−4,−1)
- Answer
-
1, 2
Exercise \(\PageIndex{20}\)
\(y=\frac{1}{3} x+1\)
- (−3,0)
- (9,4)
- (−6,−1)
Complete a Table of Solutions to a Linear Equation
In the following exercises, complete the table to find solutions to each linear equation.
Exercise \(\PageIndex{21}\)
\(y=2 x-4\)
| x | y | (x,y) |
| 0 | ||
| 2 | ||
| -1 |
- Answer
-
x y (x,y) 0 −4 (0,−4) 2 0 (2,0) −1 −6 (−1,−6)
Exercise \(\PageIndex{22}\)
\(y=3 x-1\)
| x | y | (x,y) |
| 0 | ||
| 2 | ||
| -1 |
Exercise \(\PageIndex{23}\)
\(y=-x+5\)
| x | y | (x,y) |
| 0 | ||
| 3 | ||
| -2 |
- Answer
-
x y (x,y) 0 5 (0,5) 3 2 (3,2) −2 7 (−2,7)
Exercise \(\PageIndex{24}\)
\(y=-x+2\)
| x | y | (x,y) |
| 0 | ||
| 3 | ||
| -2 |
Exercise \(\PageIndex{25}\)
\(y=\frac{1}{3} x+1\)
| x | y | (x,y) |
| 0 | ||
| 3 | ||
| 6 |
- Answer
-
x y (x,y) 0 1 (0,1) 3 2 (3,2) 6 3 (6,3)
Exercise \(\PageIndex{26}\)
\(y=\frac{1}{2} x+4\)
| x | y | (x,y) |
| 0 | ||
| 2 | ||
| 4 |
Exercise \(\PageIndex{27}\)
\(y=-\frac{3}{2} x-2\)
| x | y | (x,y) |
| 0 | ||
| 2 | ||
| -2 |
- Answer
-
x y (x,y) 0 −2 (0,−2) 2 −5 (2,−5) −2 1 (−2,1)
Exercise \(\PageIndex{28}\)
\(y=-\frac{2}{3} x-1\)
| x | y | (x,y) |
| 0 | ||
| 3 | ||
| -3 |
Exercise \(\PageIndex{29}\)
\(x+3 y=6\)
| x | y | (x,y) |
| 0 | ||
| 3 | ||
| 0 |
- Answer
-
x y (x,y) 0 2 (0,2) 3 4 (3,1) 6 0 (6,0)
Exercise \(\PageIndex{30}\)
x+2y=8
| x | y | (x,y) |
| 0 | ||
| 4 | ||
| 0 |
Exercise \(\PageIndex{31}\)
\(2 x-5 y=10\)
| x | y | (x,y) |
| 0 | ||
| 10 | ||
| 0 |
- Answer
-
x y (x,y) 0 −2 (0,−2) 10 2 (10,2) 5 0 (5,0)
Exercise \(\PageIndex{32}\)
| x | y | (x,y) |
| 0 | ||
| 8 | ||
| 0 |
Find Solutions to a Linear Equation
In the following exercises, find three solutions to each linear equation.
Exercise \(\PageIndex{33}\)
\(y=5 x-8\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{34}\)
\(y=3 x-9\)
Exercise \(\PageIndex{35}\)
\(y=-4 x+5\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{36}\)
\(y=-2 x+7\)
Exercise \(\PageIndex{37}\)
\(x+y=8\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{38}\)
\(x+y=6\)
Exercise \(\PageIndex{39}\)
\(x+y=-2\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{40}\)
\(x+y=-1\)
Exercise \(\PageIndex{41}\)
\(3 x+y=5\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{42}\)
\(2 x+y=3\)
Exercise \(\PageIndex{43}\)
\(4 x-y=8\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{44}\)
\(5 x-y=10\)
Exercise \(\PageIndex{45}\)
\(2 x+4 y=8\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{46}\)
\(3 x+2 y=6\)
Exercise \(\PageIndex{47}\)
\(5 x-2 y=10\)
- Answer
-
Answers will vary.
Exercise \(\PageIndex{48}\)
\(4 x-3 y=12\)
Everyday Math
Exercise \(\PageIndex{49}\)
Weight of a baby. Mackenzie recorded her baby’s weight every two months. The baby’s age, in months, and weight, in pounds, are listed in the table below, and shown as an ordered pair in the third column.
1. Plot the points on a coordinate plane.
2. Why is only Quadrant I needed?
| Age x | Weight y | (x,y) |
| 0 | 7 | (0, 7) |
| 2 | 11 | (2, 11) |
| 4 | 15 | (4, 15) |
| 6 | 16 | (6, 16) |
| 8 | 19 | (8, 19) |
| 10 | 20 | (10, 20) |
| 12 | 21 | (12, 21) |
- Answer
-
1.
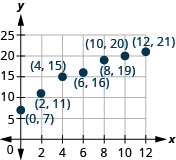
2. Age and weight are only positive.
Exercise \(\PageIndex{50}\)
Weight of a child. Latresha recorded her son’s height and weight every year. His height, in inches, and weight, in pounds, are listed in the table below, and shown as an ordered pair in the third column.
1. Plot the points on a coordinate plane.
2. Why is only Quadrant I needed?
| Height x | Weight y | (x,y) |
| 28 | 22 | (28, 22) |
| 31 | 27 | (31, 27) |
| 33 | 33 | (33, 33) |
| 37 | 35 | (37, 35) |
| 40 | 41 | (40, 41) |
| 42 | 45 | (42, 45) |
Writing Exercises
Exercise \(\PageIndex{51}\)
Explain in words how you plot the point (4,−2) in a rectangular coordinate system?
- Answer
-
Answers will vary.
Exercise \(\PageIndex{52}\)
How do you determine if an ordered pair is a solution to a given equation?
Exercise \(\PageIndex{53}\)
Is the point (−3,0) on the x-axis or y-axis? How do you know?
- Answer
-
Answers will vary.
Exercise \(\PageIndex{54}\)
Is the point (0,8) on the x-axis or y-axis? How do you know?
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
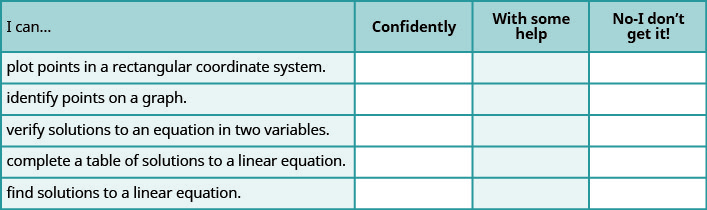
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no, I don’t get it. This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.


