4.6E: Exercises
- Last updated
- Save as PDF
- Page ID
- 30401
Practice Makes Perfect
Find an Equation of the Line Given the Slope and \(y\)-Intercept
In the following exercises, find the equation of a line with given slope and \(y\)-intercept. Write the equation in slope–intercept form.
Exercise \(\PageIndex{1}\)
slope \(3\) and \(y\)-intercept \((0,5)\)
Exercise \(\PageIndex{2}\)
slope \(4\) and \(y\)-intercept \((0,1)\)
- Answer
-
\(y=4x+1\)
Exercise \(\PageIndex{3}\)
slope \(6\) and \(y\)-intercept \((0,−4)\)
Exercise \(\PageIndex{4}\)
slope \(8\) and \(y\)-intercept \((0,−6)\)
- Answer
-
\(y=8x−6\)
Exercise \(\PageIndex{5}\)
slope \(−1\) and \(y\)-intercept \((0,3)\)
Exercise \(\PageIndex{6}\)
slope \(−1\) and \(y\)-intercept \((0,7)\)
- Answer
-
\(y=−x+7\)
Exercise \(\PageIndex{7}\)
slope \(−2\) and \(y\)-intercept \((0,−3)\)
Exercise \(\PageIndex{8}\)
slope \(−3\) and \(y\)-intercept \((0,−1)\)
- Answer
-
\(y=−3x−1\)
Exercise \(\PageIndex{9}\)
slope \(\frac{3}{5}\) and \(y\)-intercept \((0,-1)\)
Exercise \(\PageIndex{10}\)
slope \(\frac{1}{5}\) and \(y\)-intercept \((0,-5)\)
- Answer
-
\(y=\frac{1}{5} x-5\)
Exercise \(\PageIndex{11}\)
slope \(-\frac{3}{4}\) and \(y\)-intercept \((0,-2)\)
Exercise \(\PageIndex{12}\)
slope \(-\frac{2}{3}\) and \(y\)-intercept \((0,-3)\)
- Answer
-
\(y=-\frac{2}{3} x-3\)
Exercise \(\PageIndex{13}\)
slope \(0\) and \(y\)-intercept \((0,-1)\)
Exercise \(\PageIndex{14}\)
slope \(0\) and \(y\)-intercept \((0,2)\)
- Answer
-
\(y=2\)
Exercise \(\PageIndex{15}\)
slope \(-3\) and \(y\)-intercept \((0,0)\)
Exercise \(\PageIndex{16}\)
slope \(-4\) and \(y\)-intercept \((0,0)\)
- Answer
-
\(y=−4x\)
In the following exercises, find the equation of the line shown in each graph. Write the equation in slope–intercept form.
Exercise \(\PageIndex{17}\)
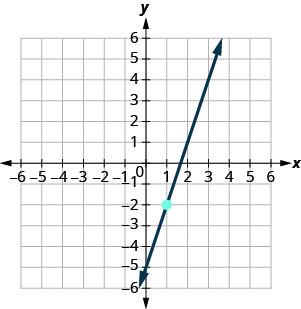
Exercise \(\PageIndex{18}\)
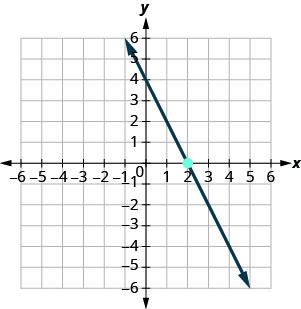
- Answer
-
\(y=−2x+4\)
Exercise \(\PageIndex{19}\)
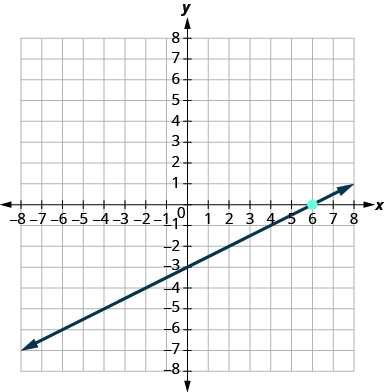
Exercise \(\PageIndex{20}\)
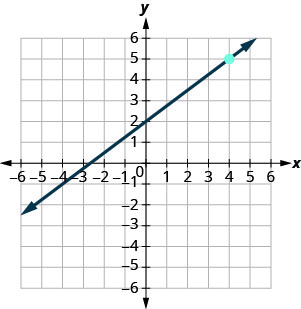
- Answer
-
\(y=\frac{3}{4} x+2\)
Exercise \(\PageIndex{21}\)
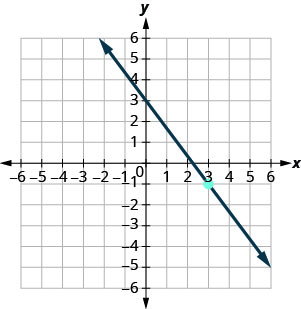
Exercise \(\PageIndex{22}\)
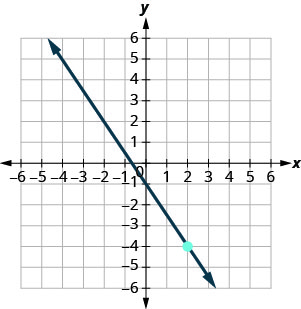
- Answer
-
\(y=-\frac{3}{2} x-1\)
Exercise \(\PageIndex{23}\)
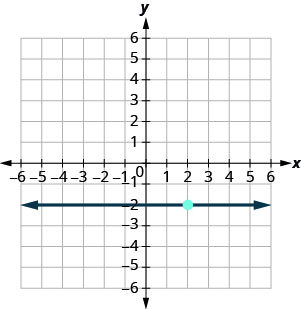
Exercise \(\PageIndex{24}\)
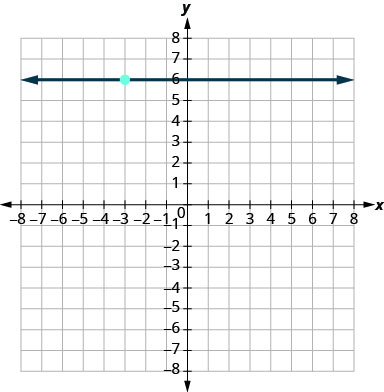
- Answer
-
\(y=6\)
Find an Equation of the Line Given the Slope and a Point
In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope–intercept form.
Exercise \(\PageIndex{25}\)
\(m=\frac{5}{8},\) point \((8,3)\)
Exercise \(\PageIndex{26}\)
\(m=\frac{3}{8},\) point \((8,2)\)
- Answer
-
\(y=\frac{3}{8} x-1\)
Exercise \(\PageIndex{27}\)
\(m=\frac{1}{6},\) point \((6,1)\)
Exercise \(\PageIndex{28}\)
\(m=\frac{5}{6},\) point \((6,7)\)
- Answer
-
\(y=\frac{5}{6} x+2\)
Exercise \(\PageIndex{29}\)
\(m=-\frac{3}{4},\) point \((8,-5)\)
Exercise \(\PageIndex{30}\)
\(m=-\frac{3}{5},\) point \((10,-5)\)
- Answer
-
\(y=-\frac{3}{5} x+1\)
Exercise \(\PageIndex{31}\)
\(m=-\frac{1}{4},\) point \((-12,-6)\)
Exercise \(\PageIndex{32}\)
\(m=-\frac{1}{3},\) point \((-9,-8)\)
- Answer
-
\(y=-\frac{1}{3} x-11\)
Exercise \(\PageIndex{33}\)
Horizontal line containing \((−2,5)\)
Exercise \(\PageIndex{34}\)
Horizontal line containing \((−1,4)\)
- Answer
-
\(y=4\)
Exercise \(\PageIndex{35}\)
Horizontal line containing \((−2,−3)\)
Exercise \(\PageIndex{36}\)
Horizontal line containing \((−1,−7)\)
- Answer
-
\(y=−7\)
Exercise \(\PageIndex{37}\)
\(m=-\frac{3}{2},\) point \((-4,-3)\)
Exercise \(\PageIndex{38}\)
\(m=-\frac{5}{2},\) point \((-8,-2)\)
- Answer
-
\(y=-\frac{5}{2} x-22\)
Exercise \(\PageIndex{39}\)
\(m=-7,\) point \((-1,-3)\)
Exercise \(\PageIndex{40}\)
\(m=-4,\) point \((-2,-3)\)
- Answer
-
\(y=-4 x-11\)
Exercise \(\PageIndex{41}\)
Horizontal line containing \((2,-3)\)
Exercise \(\PageIndex{42}\)
Horizontal line containing \((4,-8)\)
- Answer
-
\(y=−8\)
Find an Equation of the Line Given Two Points
In the following exercises, find the equation of a line containing the given points. Write the equation in slope–intercept form.
Exercise \(\PageIndex{43}\)
\((2,6)\) and \((5,3)\)
Exercise \(\PageIndex{44}\)
\((3,1)\) and \((2,5)\)
- Answer
-
\(y=−4x+13\)
Exercise \(\PageIndex{45}\)
\((4,3)\) and \((8,1)\)
Exercise \(\PageIndex{46}\)
\((2,7)\) and \((3,8)\)
- Answer
-
\(y=x+5\)
Exercise \(\PageIndex{47}\)
\((−3,−4)\) and \((5,−2)\)
Exercise \(\PageIndex{48}\)
\((−5,−3)\) and \((4,−6)\)
- Answer
-
\(y=-\frac{1}{3} x-\frac{14}{3}\)
Exercise \(\PageIndex{49}\)
\((−1,3)\) and \((−6,−7)\)
Exercise \(\PageIndex{50}\)
\((−2,8)\) and \((−4,−6)\)
- Answer
-
\(y=7x+22\)
Exercise \(\PageIndex{51}\)
\((6,−4)\) and \((−2,5)\)
Exercise \(\PageIndex{52}\)
\((3,−2)\) and \((−4,4)\)
- Answer
-
\(y=-\frac{6}{7} x+\frac{4}{7}\)
Exercise \(\PageIndex{53}\)
\((0,4)\) and \((2,−3)\)
Exercise \(\PageIndex{54}\)
\((0,−2)\) and \((−5,−3)\)
- Answer
-
\(y=\frac{1}{5} x-2\)
Exercise \(\PageIndex{55}\)
\((7,2)\) and \((7,−2)\)
Exercise \(\PageIndex{56}\)
\((4,2)\) and \((4,−3)\)
- Answer
-
\(x=4\)
Exercise \(\PageIndex{57}\)
\((−7,−1)\) and \((−7,−4)\)
Exercise \(\PageIndex{58}\)
\((−2,1)\) and \((−2,−4)\)
- Answer
-
\(x=−2\)
Exercise \(\PageIndex{59}\)
\((6,1)\) and \((0,1)\)
Exercise \(\PageIndex{60}\)
\((6,2)\) and \((−3,2)\)
- Answer
-
\(y=2\)
Exercise \(\PageIndex{61}\)
\((3,−4)\) and \((5,−4)\)
Exercise \(\PageIndex{62}\)
\((−6,−3)\) and \((−1,−3)\)
- Answer
-
\(y=−3\)
Exercise \(\PageIndex{63}\)
\((4,3)\) and \((8,0)\)
Exercise \(\PageIndex{64}\)
\((0,0)\) and \((1,4)\)
- Answer
-
\(y=4x\)
Exercise \(\PageIndex{65}\)
\((−2,−3)\) and \((−5,−6)\)
Exercise \(\PageIndex{66}\)
\((−3,0)\) and \((−7,−2)\)
- Answer
-
\(y=\frac{1}{2} x+\frac{3}{2}\)
Exercise \(\PageIndex{67}\)
\((8,−1)\) and \((8,−5)\)
Exercise \(\PageIndex{68}\)
\((3,5)\) and \((−7,5)\)
- Answer
-
\(y=5\)
Find an Equation of a Line Parallel to a Given Line
In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope–intercept form.
Exercise \(\PageIndex{69}\)
line \(y=4 x+2,\) point \((1,2)\)
Exercise \(\PageIndex{70}\)
line \(y=3 x+4,\) point \((2,5)\)
- Answer
-
\(y=3 x-1\)
Exercise \(\PageIndex{71}\)
line \(y=-2 x-3,\) point \((-1,3)\)
Exercise \(\PageIndex{72}\)
line \(y=-3x-1,\) point \((2,-3)\)
- Answer
-
\(y=−3x+3\)
Exercise \(\PageIndex{73}\)
line \(3 x-y=4,\) point \((3,1)\)
Exercise \(\PageIndex{74}\)
line \(2 x-y=6,\) point \((3,0)\)
- Answer
-
\(y=2x−6\)
Exercise \(\PageIndex{75}\)
line \(4 x+3 y=6,\) point \((0,-3)\)
Exercise \(\PageIndex{76}\)
line \(2x+3y=6,\) point \((0,5)\)
- Answer
-
\(y=-\frac{2}{3} x+5\)
Exercise \(\PageIndex{77}\)
line \(x=-3,\) point \((-2,-1)\)
Exercise \(\PageIndex{78}\)
line \(x=-4,\) point \((-3,-5)\)
- Answer
-
\(x=−3\)
Exercise \(\PageIndex{79}\)
line \(x-2=0,\) point \((1,-2)\)
Exercise \(\PageIndex{80}\)
line \(x-6=0,\) point \((4,-3)\)
- Answer
-
\(x=4\)
Exercise \(\PageIndex{81}\)
line \(y=5,\) point \((2,-2)\)
Exercise \(\PageIndex{82}\)
line \(y=1,\) point \((3,-4)\)
- Answer
-
\(y=−4\)
Exercise \(\PageIndex{83}\)
line \(y+2=0,\) point \((3,-3)\)
Exercise \(\PageIndex{84}\)
line \(y+7=0,\) point \((1,-1)\)
- Answer
-
\(y=−1\)
Find an Equation of a Line Perpendicular to a Given Line
In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope–intercept form.
Exercise \(\PageIndex{85}\)
line \(y=-2 x+3,\) point \((2,2)\)
Exercise \(\PageIndex{86}\)
line \(y=-x+5,\) point \((3,3)\)
- Answer
-
\(y=x\)
Exercise \(\PageIndex{87}\)
line \(y=\frac{3}{4} x-2,\) point \((-3,4)\)
Exercise \(\PageIndex{88}\)
line \(y=\frac{2}{3} x-4,\) point \((2,-4)\)
- Answer
-
\(y=-\frac{3}{2} x-1\)
Exercise \(\PageIndex{89}\)
line \(2 x-3 y=8,\) point \((4,-1)\)
Exercise \(\PageIndex{90}\)
line \(4 x-3 y=5,\) point \((-3,2)\)
- Answer
-
\(y=-\frac{3}{4} x-\frac{1}{4}\)
Exercise \(\PageIndex{91}\)
line \(2 x+5 y=6,\) point \((0,0)\)
Exercise \(\PageIndex{92}\)
line \(4 x+5 y=-3,\) point \((0,0)\)
- Answer
-
\(y=\frac{5}{4} x\)
Exercise \(\PageIndex{93}\)
line \(y-3=0,\) point \((-2,-4)\)
Exercise \(\PageIndex{94}\)
line \(y-6=0,\) point \((-5,-3)\)
- Answer
-
\(x=-5\)
Exercise \(\PageIndex{95}\)
line \(y\)-axis, point \((3,4)\)
Exercise \(\PageIndex{96}\)
line \(y\)-axis, point \((2,1)\)
- Answer
-
\(y=1\)
Mixed Practice
In the following exercises, find the equation of each line. Write the equation in slope–intercept form.
Exercise \(\PageIndex{97}\)
Containing the points \((4,3)\) and \((8,1)\)
Exercise \(\PageIndex{98}\)
Containing the points \((2,7)\) and \((3,8)\)
- Answer
-
\(y=x+5\)
Exercise \(\PageIndex{99}\)
\(m=\frac{1}{6},\) containing point \((6,1)\)
Exercise \(\PageIndex{100}\)
\(m=\frac{5}{6},\) containing point \((6,7)\)
- Answer
-
\(y=\frac{5}{6} x+2\)
Exercise \(\PageIndex{101}\)
Parallel to the line \(4 x+3 y=6,\) containing point \((0,-3)\)
Exercise \(\PageIndex{102}\)
Parallel to the line \(2 x+3 y=6,\) containing point \((0,5)\)
- Answer
-
\(y=-\frac{2}{3} x+5\)
Exercise \(\PageIndex{103}\)
\(m=-\frac{3}{4},\) containing point \((8,-5)\)
Exercise \(\PageIndex{104}\)
\(m=-\frac{3}{5},\) containing point \((10,-5)\)
- Answer
-
\(y=-\frac{3}{5} x+1\)
Exercise \(\PageIndex{105}\)
Perpendicular to the line \(y-1=0,\) point \((-2,6)\)
Exercise \(\PageIndex{106}\)
Perpendicular to the line y-axis, point \((-6,2)\)
- Answer
-
\(y=2\)
Exercise \(\PageIndex{107}\)
Containing the points \((4,3)\) and \((8,1)\)
Exercise \(\PageIndex{108}\)
Containing the points \((-2,0)\) and \((-3,-2)\)
- Answer
-
\(y=x+2\)
Exercise \(\PageIndex{109}\)
Parallel to the line \(x=-3,\) containing point \((-2,-1)\)
Exercise \(\PageIndex{110}\)
Parallel to the line \(x=-4,\) containing point \((-3,-5)\)
- Answer
-
\(x=-3\)
Exercise \(\PageIndex{111}\)
Containing the points \((-3,-4)\) and \((2,-5)\)
Exercise \(\PageIndex{112}\)
Containing the points \((-5,-3)\) and \((4,-6)\)
- Answer
-
\(y=-\frac{1}{3} x-\frac{14}{3}\)
Exercise \(\PageIndex{113}\)
Perpendicular to the line \(x-2 y=5,\) containing point \((-2,2)\)
Exercise \(\PageIndex{114}\)
Perpendicular to the line \(4 x+3 y=1,\) containing point \((0,0)\)
- Answer
-
\(y=\frac{3}{4} x\)
Everyday Math
Exercise \(\PageIndex{115}\)
Cholesterol. The age, \(x,\) and LDL cholesterol evel, \(y,\) of two men are given by the points \((18,68)\) and \((27,122) .\) Find a linear equation that models the relationship between age and LDL cholesterol level.
Exercise \(\PageIndex{116}\)
Fuel consumption. The city mpg, \(x\), and highway mpg, \(y,\) of two cars are given by the points \((29,40)\) and \((19,28) .\) Find a
linear equation that models the relationship between city mpg and highway mp.
- Answer
-
\(y=1.2 x+5.2\)
Writing Exercises
Exercise \(\PageIndex{117}\)
Why are all horizontal lines parallel?
Exercise \(\PageIndex{118}\)
Explain in your own words why the slopes of two perpendicular lines must have opposite signs.
- Answer
-
Answers will vary.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?


