2.2: The Commutative Property of Addition and Multiplication

Last updated
Save as PDF

Page ID: 13968

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

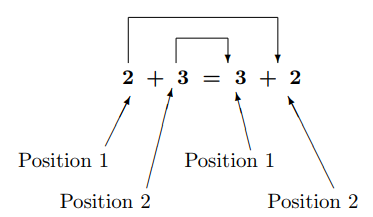
$Figure 2.2.1.png$

Figure 2.2.1

$2$ commuted (traveled) from position 1 to position 2

and

$3$ commuted (traveled) from position 2 to position 1.

Note

A commuter is a traveler. Do not say “communitive" property.

Figure 2.2.1 illustrates the commutative property of addition.

In general

\[\boxed{\Large a+b=b+a}\]

where $a$ and $b$ are any real numbers (like $-6.4$, $\displaystyle \frac{2}{7}$, $\pi$). Any real number can hide in the $a$-box or the $b$-box.

Example $\PageIndex{1}$: Is subtraction commutative?

Is $3-1=1-3$ a true statement?

Solution

No, because $3-1-2$ and $1-3=-2$. If we find one counterexample, one example that shows that subtraction is not commutative, the general property (using $a$ and $b$) does not exist.

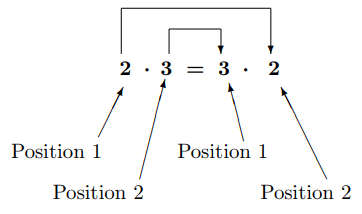
$Figure 2.2.2.png$

Figure 2.2.2

$2$ commuted (traveled) from position 1 to position 2

and

$3$ commuted (traveled) from position 2 to position 1.

Figure 2.2.2 illustrates the commutative property of multiplication.

In general

\[\boxed{\Large ab=ba}\]

where $a$ and $b$ are any real numbers (like $-6.4$, $\displaystyle \frac{2}{7}$, $\pi$). Any real number can hide in the $a$-box or the $b$-box.

Note that $ab$ means $a$ times $b$.

Example $\PageIndex{2}$: Is division commutative?

Is $4\div 2=2\div 4$ a true statement?

Solution

No, because $4\div 2=2$ and $2\div 4=\displaystyle \frac{1}{2}=0.5$. If we find one counterexample, one example that shows that division is not commutative, the general property (using $a$ and $b$) does not exist