5.1: Fluid Force

Fluid Pressure

We define the fluid pressure $P$ to be equal to the weight (force) density $w$ times the depth of the fluid $h$:

$$P = wh. \nonumber$$

Pascal's Principle

The pressure is equal in all directions (isotropic).

Since

$$\text{Pressure} = \dfrac{\text{force}}{\text{area}} \nonumber$$

we have Pascal's Principle

$$F = PA. \nonumber$$

Force on a Submerged Rectangular Sheet

Example 1

Suppose that a glass sheet lies parallel to and five feet below the surface of a lake has dimensions 2 by 3.

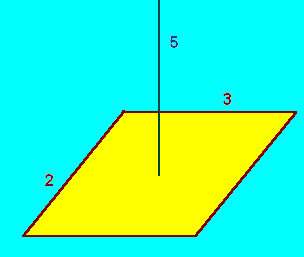
Then the total pressure on the sheet is

$$P = wh = (62.4)(5) = 312. \nonumber$$

The total force on the plate is

$$\begin{align} PA &= (312)(6) \\ &= 1872. \end{align} \nonumber$$

Force on a Vertical Surface

Example 2

A 3 x 2 square window on the new Disney Cruise liner is to be built so that top of the window is four feet below the surface of the water. What total force will the window be subjected to?

Solution

We take horizontal cross sections. Letting $y$ be the distance from the top of the window to the cross section, we have

$$\Delta{F} = 62.4 \frac{(4 + y)}{\Delta{A}} = 62.4\dfrac{4 + y}{3 \, \Delta{y}}. \nonumber$$

Hence the total force is

$$\begin{align} F&=\int_0^2 62.4(4-y)(3) \; dy \\ &= 187.2\left(4y-\dfrac{1}{2}y^2\right]_0^2 \\ &= 187.2[8-2] \\ &= 1123.2 \text{ pounds}. \end{align} \nonumber$$

In general:

$$\int_a^b w(\text{height})(\text{cross sectional length}) \; dy. \nonumber$$

Example 3

A radius 2 feet circular portal is vertically submerged so that its center is 20 feet below the surface of the water. Find the total force of the water on the portal.

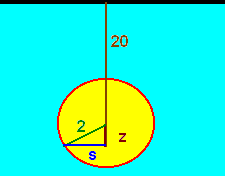
Solution

We write $s$ in terms of $z$ by the Pythagorean theorem:

$$s=\sqrt{4-z^2}. \nonumber$$

This horizontal cross-section has area

$$DA=2sDz. \nonumber$$

The depth at this cross-section is

$$h=20+z. \nonumber$$

We put this all together to find the force

$$\begin{align} F&=\int_{-2}^{2} (2\sqrt{4-z^2})(20+z) \; dz \\ &= 40\int_{-2}^{2} \sqrt{4-z^2} \; dz + 2\int_{-2}^{2} z\sqrt{4-z^2} \; dz. \end{align} \nonumber$$

We recognize the first integral as the area of the semi-circle of radius 2. Use U-substitution to solve the second integral, let

$$u = 4 - z^2\;\;\; \text{with} \;\;\;du = -2z \; dz \nonumber$$

Notice that when $z = -2$, $u = 0$ and when $z = 2$, $u = 0$ also. Any integral with lower and upper limits the same is always zero. Hence the force is

$$F = 40\, \pi, 2^2 + 0 = 160\, \pi \nonumber$$

Exercise

In the VIP suite, the glass window is in the shape of an equilateral triangle with diagonal length 2 such that the top of the triangle is submerged 5 feet below the water. What total force will this window be subjected to?

Contributors and Attributions

• Larry Green (Lake Tahoe Community College)

• Integrated by Justin Marshall.