1.E: Vectors in Euclidian Space (Exercises)
- Page ID
- 3077
1.1: Introduction
A
1.1.1. Calculate the magnitudes of the following vectors:\(\text{(a) } \textbf{v} = (2,-1) \quad \text{(b) } \textbf{v} = (2,-1,0) \quad \text{(c) } \textbf{v} = (3,2,-2) \quad \text{(d) }\textbf{v} = (0,0,1) \quad \text{ (e) } \textbf{v} = (6,4,-4)\)
1.1.2. For the points \(P =(1,-1,1)\), \(Q=(2,-2,2)\), \(R=(2,0,1)\), \(S=(3,-1,2)\), does \(\overrightarrow{PQ} = \overrightarrow{RS}\)?
1.1.3 For the points \(P =(0,0,0)\), \(Q=(1,3,2)\), \(R=(1,0,1)\), \(S=(2,3,4)\), does \(\overrightarrow{PQ} = \overrightarrow{RS}\)?
B
1.1.4 Let \(\textbf{v} = (1,0,0)\) and \(\textbf{w} = (a,0,0)\) be vectors in \(\mathbb{R}^{3}\). Show that \(\norm{\textbf{w}} = |a| \,\norm{\textbf{v}}\).
1.1.5 Let \(\textbf{v} = (a,b,c)\) and \(\textbf{w} = (3a,3b,3c)\) be vectors in \(\mathbb{R}^{3}\). Show that \(\norm{\textbf{w}} = 3 \,\norm{\textbf{v}}\).
C
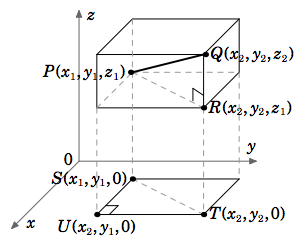
Figure 1.1.9
1.1.6 Though we will see a simple proof of Theorem 1.1 in the next section, it is possible to prove it using methods similar to those in the proof of Theorem 1.2. Prove the special case of Theorem 1.1 where the points \(P = (x_{1}, y_{1}, z_{1})\) and \(Q = x_{2}, y_{2}, z_{2})\) satisfy the following conditions:
\(x_{2} > x_{1} > 0\), \(y_{2} > y_{1} > 0\), and \(z_{2} > 1 > 0\).
\(\textit{Hint: Think of Case 4 in the proof of Theorem (1.2), and consider Figure 1.1.9.}\)
1.2: Vector Algebra
A
1.2.1 Let \(\textbf{v} = (-1,5,-2)\) and \(\textbf{w} = (3,1,1)\).
- Find \(\textbf{v} - \textbf{w}\).
- Find \(\textbf{v} + \textbf{w}\).
- Find \(\frac{\textbf{v}}{\norm{\textbf{v}}}\).
- Find \(\norm{\frac{1}{2}(\textbf{v} - \textbf{w})}\).
- Find \(\norm{\frac{1}{2}(\textbf{v} + \textbf{w})}\).
- Find \(-2\,\textbf{v} + 4\,\textbf{w}\).
- Find \(\textbf{v} - 2\,\textbf{w}\).
- Find the vector \(\textbf{u}\) such that \(\textbf{u} + \textbf{v} + \textbf{w} = \textbf{i}\).
- Find the vector \(\textbf{u}\) such that \(\textbf{u} + \textbf{v} + \textbf{w} = 2\,\textbf{j} + \textbf{k}\).
- Is there a scalar \(m\) such that \(m(\textbf{v} + 2\,\textbf{w}) = \textbf{k}\)? If so, find it.
1.2.2. For the vectors \(\textbf{v}\) and \(\textbf{w}\) from Exercise 1, is \(\norm{\textbf{v} - \textbf{w}} = \norm{\textbf{v}} - \norm{\textbf{w}}\)? If not, which quantity is larger?
1.2.3. For the vectors \(\textbf{v}\) and \(\textbf{w}\) from Exercise 1, is \(\norm{\textbf{v} + \textbf{w}} = \norm{\textbf{v}} + \norm{\textbf{w}}\)? If not, which quantity is larger?
B
1.2.4. Prove Theorem 1.5 (f) for \(\mathbb{R}^{3}\).
1.2.5. Prove Theorem 1.5 (g) for \(\mathbb{R}^{3}\).
C
1.2.6. We know that every vector in \(\mathbb{R}^{3}\) can be written as a scalar combination of the vectors \(\textbf{i}\), \(\textbf{j}\), and \(\textbf{k}\). Can every vector in \(\mathbb{R}^{3}\) be written as a scalar combination of just \(\textbf{i}\) and \(\textbf{j}\), i.e. for any vector \(\textbf{v}\) in \(\mathbb{R}^{3}\), are there scalars \(m\), \(n\) such that \(\textbf{v} = m\,\textbf{i} + n\,\textbf{j}\)? Justify your answer.
1.3: Dot Product
A
1.3.1. Let \(\textbf{v} = (5,1,-2)\) and \(\textbf{w} = (4,-4,3)\). Calculate \(\textbf{v} \cdot \textbf{w}\).
1.3.2. Let \(\textbf{v} = -3\,\textbf{i} - 2\,\textbf{j} - \textbf{k}\) and \(\textbf{w} = 6\,\textbf{i} + 4\,\textbf{j} + 2\,\textbf{k}\). Calculate \(\textbf{v} \cdot \textbf{w}\).
For Exercises 3-8, find the angle \(\theta\) between the vectors \(\textbf{v}\) and \(\textbf{w}\).
1.3.3. \(\textbf{v} = (5,1,-2)\), \(\textbf{w} = (4,-4,3)\)
1.3.4. \(\textbf{v} = (7,2,-10)\), \(\textbf{w} = (2,6,4)\)
1.3.5. \(\textbf{v} = (2,1,4)\), \(\textbf{w} = (1,-2,0)\)
1.3.6. \(\textbf{v} = (4,2,-1)\), \(\textbf{w} = (8,4,-2)\)
1.3.7. \(\textbf{v} = -\,\textbf{i} + 2\,\textbf{j} + \textbf{k}\), \(\textbf{w} = -3\,\textbf{i} + 6\,\textbf{j} + 3\,\textbf{k}\)
1.3.8. \(\textbf{v} = \textbf{i}\), \(\textbf{w} = 3\,\textbf{i} + 2\,\textbf{j} + 4\textbf{k}\)
1.3.9. Let \(\textbf{v} = (8,4,3)\) and \(\textbf{w} = (-2,1,4)\). Is \(\textbf{v} \perp \textbf{w}\)? Justify your answer.
1.3.10. Let \(\textbf{v} = (6,0,4)\) and \(\textbf{w} = (0,2,-1)\). Is \(\textbf{v} \perp \textbf{w}\)? Justify your answer.
1.3.11. For \(\textbf{v}\), \(\textbf{w}\) from Exercise 5, verify the Cauchy-Schwarz Inequality \(|\textbf{v} \cdot \textbf{w}| \le \norm{\textbf{v}}\,\norm{\textbf{w}}\).
1.3.12. For \(\textbf{v}\), \(\textbf{w}\) from Exercise 6, verify the Cauchy-Schwarz Inequality \(|\textbf{v} \cdot \textbf{w}| \le \norm{\textbf{v}}\,\norm{\textbf{w}}\).
1.3.13. For \(\textbf{v}\), \(\textbf{w}\) from Exercise 5, verify the Triangle Inequality \(\norm{\textbf{v} + \textbf{w}} \le \norm{\textbf{v}} + \norm{\textbf{w}}\).
1.3.14. For \(\textbf{v}\), \(\textbf{w}\) from Exercise 6, verify the Triangle Inequality \(\norm{\textbf{v} + \textbf{w}} \le \norm{\textbf{v}} + \norm{\textbf{w}}\).
B
Note: Consider only vectors in \(\mathbb{R}^{3}\) for Exercises 15-25.
1.3.15. Prove Theorem 1.9 (a).
1.3.16. Prove Theorem 1.9 (b).
1.3.17. Prove Theorem 1.9 (c).
1.3.18. Prove Theorem 1.9 (d).
1.3.19. Prove Theorem 1.9 (e).
1.3.20. Prove Theorem 1.10 (a).
1.3.21. Prove or give a counterexample: If \(\textbf{u} \cdot \textbf{v} = \textbf{u} \cdot \textbf{w}\), then \(\textbf{v} =\textbf{w}\).
C
1.3.22. Prove or give a counterexample: If \(\textbf{v} \cdot \textbf{w} = 0\) for all \(\textbf{v}\), then \(\textbf{w} =\textbf{0}\).
1.3.23. Prove or give a counterexample: If \(\textbf{u} \cdot \textbf{v} = \textbf{u} \cdot \textbf{w}\) for all \(\textbf{u}\), then \(\textbf{v} = \textbf{w}\).
1.3.24. Prove that \(|\norm{\textbf{v}} - \norm{\textbf{w}}| \le \norm{\textbf{v} - \textbf{w}}\) for all \(\textbf{v}, \textbf{w}\).
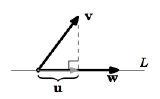
Figure 1.3.5
1.3.25. For nonzero vectors \(\textbf{v}\) and \(\textbf{w}\), the \(\textit{projection}\) of \(\textbf{v}\) onto \(\textbf{w}\) (sometimes written as \(proj_{\textbf{w}}\textbf{v}\)) is the vector \(\textbf{u}\) along the same line \(L\) as \(\textbf{w}\) whose terminal point is obtained by dropping a perpendicular line from the terminal point of \(\textbf{v}\) to \(L\) (see Figure 1.3.5). Show that
\[\norm{\textbf{u}} = \frac{|\textbf{v} \cdot \textbf{w}|}{\norm{\textbf{w}}}.\]
\(\textit{(Hint: Consider the angle between}\) \(\textbf{v}\) \(\textit{and}\) \(\textbf{w}\).\(\textit{)}\)
1.3.26. Let \(\alpha\), \(\beta\), and \(\gamma\) be the angles between a nonzero vector \(\textbf{v}\) in \(\mathbb{R}^{3}\) and the vectors \(\textbf{i}\), \(\textbf{j}\), and \(\textbf{k}\), respectively. Show that \(\cos^{2} \alpha + \cos^{2} \beta + \cos^{2} \gamma = 1\).
(Note: \(\alpha\), \(\beta\), \(\gamma\) are often called the \(\textit{direction angles}\) of \(\textbf{v}\), and \(\cos \alpha\), \(\cos \beta\), \(\cos \gamma\) are called the \(\textit{direction cosines}\).)
1.4: Cross Product
A
For Exercises 1-6, calculate \(\textbf{v} \times \textbf{w}\).
1.4.1. \(\textbf{v} = (5,1,-2)\), \(\textbf{w} = (4,-4,3)\)
1.4.2. \(\textbf{v} = (7,2,-10)\), \(\textbf{w} = (2,6,4)\)
1.4.3. \(\textbf{v} = (2,1,4)\), \(\textbf{w} = (1,-2,0)\)
1.4.4. \(\textbf{v} = (1,3,2)\), \(\textbf{w} = (7,2,-10)\)
1.4.5. \(\textbf{v} = -\,\textbf{i} + 2\,\textbf{j} + \textbf{k}\), \(\textbf{w} = -3\,\textbf{i} + 6\,\textbf{j} + 3\,\textbf{k}\)
1.4.6. \(\textbf{v} = \textbf{i}\), \(\textbf{w} = 3\,\textbf{i} + 2\,\textbf{j} + 4\textbf{k}\)
For Exercises 7-8, calculate the area of the triangle \(\triangle PQR\).
1.4.7. \(P = (5,1,-2)\), \(Q = (4,-4,3)\), \(R =(2,4,0)\)
1.4.8. \(P = (4,0,2)\), \(Q = (2,1,5)\), \(R =(-1,0,-1)\)
For Exercises 9-10, calculate the area of the parallelogram \(PQRS\).
1.4.9. \(P = (2,1,3)\), \(Q = (1,4,5)\), \(R = (2,5,3)\), \(S = (3,2,1)\)
1.4.10. \(P = (-2,-2)\), \(Q = (1,4)\), \(R = (6,6)\), \(S = (3,0)\)
For Exercises 11-12, find the volume of the parallelepiped with adjacent sides \(\textbf{u}, \textbf{v}, \textbf{w}\).
1.4.11. \(\textbf{u} = (1,1,3)\), \(\textbf{v} = (2,1,4)\), \(\textbf{w} = (5,1,-2)\)
1.4.12. \(\textbf{u} = (1,3,2)\), \(\textbf{v} = (7,2,-10)\), \(\textbf{w} = (1,0,1)\)
For Exercises 13-14, calculate \(\textbf{u} \cdot (\textbf{v} \times \textbf{w})\) and \(\textbf{u} \times (\textbf{v} \times \textbf{w})\).
1.4.13. \(\textbf{u} = (1,1,1)\), \(\textbf{v} = (3,0,2)\), \(\textbf{w} = (2,2,2)\)
1.4.14. \(\textbf{u} = (1,0,2)\), \(\textbf{v} = (-1,0,3)\), \(\textbf{w} = (2,0,-2)\)
1.4.15. Calculate \((\textbf{u} \times \textbf{v}) \cdot (\textbf{w} \times \textbf{z})\) for \(\textbf{u} = (1,1,1)\), \(\textbf{v} = (3,0,2)\), \(\textbf{w} = (2,2,2)\), \(\textbf{z} = (2,1,4)\).
B
1.4.16. If \(\textbf{v}\) and \(\textbf{w}\) are unit vectors in \(\mathbb{R}^{3}\), under what condition(s) would \(\textbf{v} \times \textbf{w}\) also be a unit vector in \(\mathbb{R}^{3}\;\)? Justify your answer.
1.4.17. Show that if \(\textbf{v} \times \textbf{w} = \textbf{0}\) for all \(\textbf{w}\) in \(\mathbb{R}^{3}\), then \(\textbf{v} = \textbf{0}\).
1.4.18. Prove Theorem 1.14(b).
1.4.19. Prove Theorem 1.14(c).
1.4.20. Prove Theorem 1.14(d).
1.4.21. Prove Theorem 1.14(e).
1.4.22. Prove Theorem 1.14(f).
1.4.23. Prove Theorem 1.16.
1.4.24. Prove Theorem 1.17. (Hint: Expand both sides of the equation.)
1.4.25. Prove the following for all vectors \(\textbf{v}, \,\textbf{w}\text{ in }\mathbb{R}^ 3\):
(a) \(\norm{\textbf{v} \times \textbf{w}}^{2} + | \textbf{v} \cdot \textbf{w}|^{2} = \norm{\textbf{v}}^2 \, \norm{\textbf{w}}^2 \)
(b) If \(\textbf{v} \cdot \textbf{w} = 0\) and \(\textbf{v} \times \textbf{w} = \textbf{0}\), then \(\textbf{v} = \textbf{0}\) or \(\textbf{w} = \textbf{0}\).
C
1.4.26. Prove that in Example 1.8 the formula for the area of the triangle \(\triangle PQR\) yields the same value no matter which two adjacent sides are chosen. To do this, show that \(\frac{1}{2}\,\norm{\textbf{u} \times (-\textbf{w})} = \frac{1}{2}\,\norm{\textbf{v} \times \textbf{w}}\), where \(\textbf{u} = PR\), \(-\textbf{w} = PQ\), and \(\textbf{v} = QR\), \(\textbf{w} = QP\) as before. Similarly, show that \(\frac{1}{2}\,\norm{(-\textbf{u}) \times (-\textbf{v})} = \frac{1}{2}\,\norm{\textbf{v} \times \textbf{w}}\), where \(-\textbf{u} = RP\) and \(-\textbf{v} = RQ\).
1.4.27. Consider the vector equation \(\textbf{a} \times \textbf{x} = \textbf{b}\) in \(\mathbb{R}^{3}\), where \(\textbf{a} \ne \textbf{0}\). Show that:
- \(\textbf{a} \cdot \textbf{b} = 0\)
- \(\textbf{x} = \dfrac{\textbf{b} \times \textbf{a}}{\norm{\textbf{a}}^{2}} + k \textbf{a}\) is a solution to the equation, for any scalar \(k\).
1.4.28. Prove the \(\textit{Jacobi identity}\):
$$\textbf{u} \times (\textbf{v} \times \textbf{w}) + \textbf{v} \times (\textbf{w} \times \textbf{u}) + \textbf{w} \times (\textbf{u} \times \textbf{v}) = \textbf{0}\]
1.4.29. Show that \(\textbf{u}, \textbf{v}, \textbf{w}\) lie in the same plane in \(\mathbb{R}^{3}\) if and only if \(\textbf{u} \cdot (\textbf{v} \times \textbf{w}) = 0\).
1.4.30. For all vectors \(\textbf{u}, \textbf{v}, \textbf{w}, \textbf{z}\) in \(\mathbb{R}^{3}\), show that
\[(\textbf{u} \times \textbf{v}) \times (\textbf{w} \times \textbf{z}) =
(\textbf{z} \cdot (\textbf{u} \times \textbf{v}))\textbf{w} -
(\textbf{w} \cdot (\textbf{u} \times \textbf{v}))\textbf{z}\]
and that
\[(\textbf{u} \times \textbf{v}) \times (\textbf{w} \times \textbf{z}) =
(\textbf{u} \cdot (\textbf{w} \times \textbf{z}))\textbf{v} -
(\textbf{v} \cdot (\textbf{w} \times \textbf{z}))\textbf{u}\]
Why do both equations make sense geometrically?
Contributors and Attributions
Michael Corral (Schoolcraft College). The content of this page is distributed under the terms of the GNU Free Documentation License, Version 1.2.

