1.3: Dot Product

You may have noticed that while we did define multiplication of a vector by a scalar in the previous section on vector algebra, we did not define multiplication of a vector by a vector. We will now see one type of multiplication of vectors, called the dot product.

Definition 1.6: Dot Product

Let $\textbf{v} = (v_{1}, v_{2}, v_{3})$ and $\textbf{w}$ = $(w_{1}, w_{2}, w_{3})$ be vectors in $\mathbb{R}^{3}$. The $\textbf{dot product}$ of $\textbf{v}$ and $\textbf{w}$, denoted by $\textbf{v} \cdot \textbf{w}$, is given by:

$$\textbf{v} \cdot \textbf{w} = v_{1}w_{1} + v_{2}w_{2} + v_{3}w_{3}$$

Similarly, for vectors $\textbf{v} = (v_{1}, v_{2})$ and $\textbf{w} = (w_{1}, w_{2})$ in $\mathbb{R}^{2}$, the dot product is:

$$\textbf{v} \cdot \textbf{w} = v_{1}w_{1} + v_{2}w_{2}$$

Notice that the dot product of two vectors is a scalar, not a vector. So the associative law that holds for multiplication of numbers and for addition of vectors (see Theorem 1.5 (b),(e)), does $\textit{not}$ hold for the dot product of vectors. Why? Because for vectors $\textbf{u}$, $\textbf{v}$, $\textbf{w}$, the dot product $\textbf{u} \cdot \textbf{v}$ is a scalar, and so $(\textbf{u} \cdot \textbf{v}) \cdot \textbf{w}$ is not defined since the left side of that dot product (the part in parentheses) is a scalar and not a vector.

For vectors $\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k}$ and $\textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j} + w_{3}\textbf{k}$ in component form, the dot product is still $\textbf{v} \cdot \textbf{w} = v_{1}w_{1} + v_{2}w_{2} + v_{3}w_{3}$.

Also notice that we defined the dot product in an analytic way, i.e. by referencing vector coordinates. There is a geometric way of defining the dot product, which we will now develop as a consequence of the analytic definition.

Definition 1.7

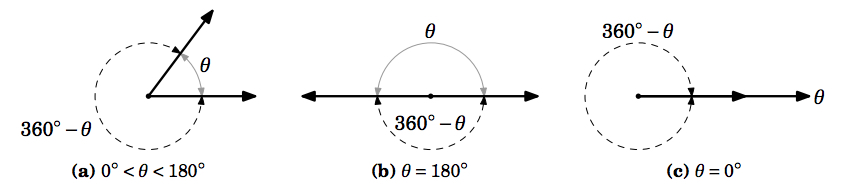
The $\textbf{angle}$ between two nonzero vectors with the same initial point is the smallest angle between them.

We do not define the angle between the zero vector and any other vector. Any two nonzero vectors with the same initial point have two angles between them: $\theta$ and $360^{\circ} - \theta$. We will always choose the smallest nonnegative angle $\theta$ between them, so that $0^{\circ} \leq \theta \leq 180^{\circ}$. See Figure 1.3.1.

Figure 1.3.1 Angle between vectors

We can now take a more geometric view of the dot product by establishing a relationship between the dot product of two vectors and the angle between them.

Theorem 1.6

Let $\textbf{v}$, $\textbf{w}$ be nonzero vectors, and let $\theta$ be the angle between them. Then

$$\cos \theta = \dfrac{\textbf{v} \cdot \textbf{w}}{\norm{\textbf{v}}\, \norm{\textbf{w}}}$$

Proof

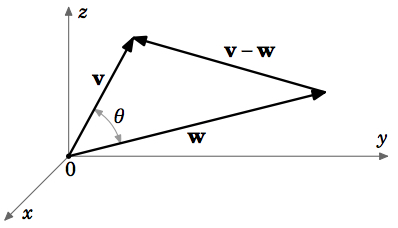
We will prove the theorem for vectors in $\mathbb{R}^{3}$ (the proof for $\mathbb{R}^{2}$ is similar). Let $\textbf{v} = (v_{1}, v_{2}, v_{3})$ and $\textbf{w} = (w_{1}, w_{2}, w_{3})$. By the Law of Cosines (see Figure 1.3.2), we have

$$\norm{\textbf{v} - \textbf{w}}^{2} = \norm{\textbf{v}}^{2} + \norm{\textbf{w}}^{2} - 2\,\norm{\textbf{v}}\,\norm{\textbf{w}} \cos \theta \label{Equation 1.3.3}$$

(note that Equation $\ref{Equation 1.3.3}$) holds even for the "degenerate'' cases $\theta = 0^{\circ}$ and $180^{\circ}$).

Figure 1.3.2

Since $\textbf{v} - \textbf{w} = (v_{1} - w_{1}, v_{2} - w_{2}, v_{3} - w_{3})$, expanding $\norm{\textbf{v} - \textbf{w}}^{2}$ in Equation $\ref{Equation 1.3.3}$ gives

$$\nonumber \begin{align} \norm{\textbf{v}}^{2} + \norm{\textbf{w}}^{2} - 2\,\norm{\textbf{v}}\,\norm{\textbf{w}} \cos \theta &= (v_{1} - w_{1})^{2} + (v_{2} - w_{2})^{2} + (v_{3} - w_{3})^{2} \\[4pt] \nonumber&= (v_{1}^{2} - 2v_{1}w_{1} + w_{1}^{2}) + (v_{2}^{2} - 2v_{2}w_{2} +w_{2}^{2}) + (v_{3}^{2} - 2v_{3}w_{3} + w_{3}^{2}) \\[4pt] \nonumber&= (v_{1}^{2} + v_{2}^{2} + v_{3}^{2}) + (w_{1}^{2} + w_{2}^{2} + w_{3}^{2}) - 2(v_{1}w_{1} + v_{2}w_{2} + v_{3}w_{3}) \\[4pt] \nonumber&= \norm{\textbf{v}}^{2} + \norm{\textbf{w}}^{2} - 2(\textbf{v} \cdot \textbf{w}) \text{, so} \\[4pt] \nonumber -2\,\norm{\textbf{v}}\,\norm{\textbf{w}} \cos \theta &= -2(\textbf{v} \cdot \textbf{w}) \text{, so since }\textbf{v} \neq \textbf{0} \text{ and }\textbf{w} \neq \textbf{0} \text{ then} \\[4pt] \nonumber \cos \theta &= \dfrac{\textbf{v} \cdot \textbf{w}}{\norm{\textbf{v}} \norm{\textbf{w}}} \text{, since} \norm{\textbf{v}} > 0 \text{ and } \norm{\textbf{w}} > 0. \\[4pt] \end{align}$$

Example 1.5

Find the angle $\theta$ between the vectors $\textbf{v} = (2,1,-1)$ and $\textbf{w} = (3,-4,1)$.

Solution

Since $\textbf{v} \cdot \textbf{w} = (2)(3) + (1)(-4) + (-1)(1) = 1$, $\norm{\textbf{v}} = \sqrt{6}$, and $\norm{\textbf{w}} = \sqrt{26}$, then

$$\cos \theta = \frac{\textbf{v} \cdot \textbf{w}}{\norm{\textbf{v}} \, \norm{\textbf{w}}} = \frac{1}{\sqrt{6}\,\sqrt{26}} = \frac{1}{2 \sqrt{39}} \approx 0.08 ~ \Longrightarrow ~ \theta = 85.41^{\circ}.\nonumber$$

Two nonzero vectors are $\textbf{perpendicular}$ if the angle between them is $90^{\circ}$. Since $\cos 90^{\circ} = 0$, we have the following important corollary to Theorem 1.6:

Corollary 1.7

Two nonzero vectors $\textbf{v}$ and $\textbf{w}$ are perpendicular if and only if $\textbf{v} \cdot \textbf{w} = 0$.

We will write $\textbf{v} \perp \textbf{w}$ to indicate that $\textbf{v}$ and $\textbf{w}$ are perpendicular.

Since $\cos \theta > 0$ for $0^{\circ} \le \theta < 90^{\circ}$ and $\cos \theta < 0$ for $90^{\circ} < \theta \le 180^{\circ}$, we also have:

Corollary 1.8

If $\theta$ is the angle between nonzero vectors $\textbf{v}$ and $\textbf{w}$, then

$$\nonumber \textbf{v} \cdot \textbf{w} \text{ is }= \begin{cases} > 0, & \text{for }0^{\circ} \leq \theta < 90^{\circ} \\[4pt] 0, & \text{for }\theta = 90^{\circ} \\[4pt] < 0, & \text{for } 90^{\circ} < \theta \leq 180^{\circ}\end{cases}$$

By Corollary 1.8, the dot product can be thought of as a way of telling if the angle between two vectors is acute, obtuse, or a right angle, depending on whether the dot product is positive, negative, or zero, respectively. See Figure 1.3.3.

Figure 1.3.3 Sign of the dot product & angle between vectors

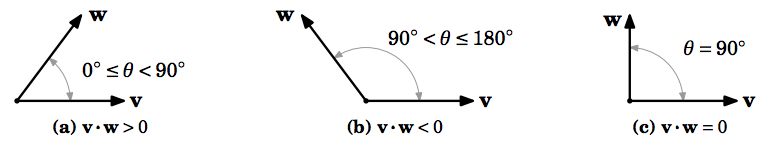
Example 1.6

Are the vectors $\textbf{v} = (-1,5,-2)$ and $\textbf{w} = (3,1,1)$ perpendicular?

Solution

Yes, $\textbf{v} \perp \textbf{w}$ since $\textbf{v} \cdot \textbf{w} = (-1)(3) + (5)(1) + (-2)(1) = 0$.

The following theorem summarizes the basic properties of the dot product.

Theorem 1.9: Basic Properties of the Dot Product

For any vectors $\textbf{u}, \textbf{v}, \textbf{w}$, and scalar $k$, we have

1. $\textbf{v} \cdot \textbf{w} = \textbf{w} \cdot \textbf{v}$ Commutative Law
2. $(k\textbf{v}) \cdot \textbf{w} = \textbf{v} \cdot (k\textbf{w}) = k(\textbf{v} \cdot \textbf{w})$ Associative Law
3. $\textbf{v} \cdot \textbf{0} = 0 = \textbf{0} \cdot \textbf{v}$
4. $\textbf{u} \cdot (\textbf{v} + \textbf{w}) = \textbf{u} \cdot \textbf{v} + \textbf{u} \cdot \textbf{w}$ Distributive Law
5. $(\textbf{u} + \textbf{v}) \cdot \textbf{w} = \textbf{u} \cdot \textbf{w} + \textbf{v} \cdot \textbf{w}$ Distributive Law
6. $|\textbf{v} \cdot \textbf{w}| \le \norm{\textbf{v}}\,\norm{\textbf{w}}$ Cauchy-Schwarz Inequality

Proof

The proofs of parts (a)-(e) are straightforward applications of the definition of the dot product, and are left to the reader as exercises. We will prove part (f).

(f) If either $\textbf{v} = \textbf{0}$ or $\textbf{w} = \textbf{0}$, then $\textbf{v} \cdot \textbf{w} = 0$ by part (c), and so the inequality holds trivially. So assume that $\textbf{v}$ and $\textbf{w}$ are nonzero vectors. Then by Theorem 1.6,

$$\nonumber \begin{align} \textbf{v} \cdot \textbf{w} &= \cos \theta\,\norm{\textbf{v}}\,\norm{\textbf{w}}\text{, so} \\[4pt] \nonumber |\textbf{v} \cdot \textbf{w}| &= |\cos \theta| \, \norm{\textbf{v}}\,\norm{\textbf{w}} \text{, so} \\[4pt] \nonumber |\textbf{v} \cdot \textbf{w}| &\le \norm{\textbf{v}}\,\norm{\textbf{w}} \text{ since }|\cos \theta| \le 1. \\[4pt] \end{align}$$

Using Theorem 1.9, we see that if $\textbf{u} \cdot \textbf{v} = 0$ and $\textbf{u} \cdot \textbf{w} = 0$, then $\textbf{u} \cdot (k\textbf{v} + l\textbf{w}) = k(\textbf{u} \cdot \textbf{v}) + l(\textbf{u} \cdot \textbf{w}) = k(0) + l(0) =0$ for all scalars $k, l$. Thus, we have the following fact:

$$\nonumber \text{If \(\textbf{u} \perp \textbf{v}\) and \(\textbf{u} \perp \textbf{w}\), then \(\textbf{u} \perp (k\textbf{v} + l\textbf{w})\) for all scalars \(k, l\).}$$

For vectors $\textbf{v}$ and $\textbf{w}$, the collection of all scalar combinations $k\textbf{v} + l\textbf{w}$ is called the $\textbf{span}$ of $\textbf{v}$ and $\textbf{w}$. If nonzero vectors $\textbf{v}$ and $\textbf{w}$ are parallel, then their span is a line; if they are not parallel, then their span is a plane. So what we showed above is that a vector which is perpendicular to two other vectors is also perpendicular to their span.

The dot product can be used to derive properties of the magnitudes of vectors, the most important of which is the $\textit{Triangle Inequality}$, as given in the following theorem:

Theorem 1.10: Vector Magnitude Limitations

For any vectors $\textbf{v}, \textbf{w}$, we have

1. $\norm{\textbf{v}}^{2} = \textbf{v} \cdot \textbf{v}$
2. $\norm{\textbf{v} + \textbf{w}} \le \norm{\textbf{v}} + \norm{\textbf{w}}$ Triangle Inequality
3. $\norm{\textbf{v} - \textbf{w}} \ge \norm{\textbf{v}} - \norm{\textbf{w}}$

Proof:
(a) Left as an exercise for the reader.

(b) By part (a) and Theorem 1.9, we have
$$\begin{align*} \norm{\textbf{v} + \textbf{w}}^{2} &= (\textbf{v} + \textbf{w}) \cdot (\textbf{v} + \textbf{w}) = \textbf{v} \cdot \textbf{v} + \textbf{v} \cdot \textbf{w} + \textbf{w} \cdot \textbf{v} + \textbf{w} \cdot \textbf{w}\\[4pt] &= \norm{\textbf{v}}^{2} + 2(\textbf{v} \cdot \textbf{w}) + \norm{\textbf{w}}^{2} \text{, so since \(a \le |a|\) for any real number \(a\), we have}\\[4pt] &\le \norm{\textbf{v}}^{2} + 2\,|\textbf{v} \cdot \textbf{w}| + \norm{\textbf{w}}^{2} \text{, so by Theorem 1.9(f) we have}\\[4pt] &\le \norm{\textbf{v}}^{2} + 2\,\norm{\textbf{v}}\,\norm{\textbf{w}} + \norm{\textbf{w}}^{2} = (\norm{\textbf{v}} + \norm{\textbf{w}})^{2} \text{and so}\\[4pt] \norm{\textbf{v} + \textbf{w}} &\le \norm{\textbf{v}} + \norm{\textbf{w}} \text{after taking square roots of both sides, which proves (b).} \end{align*}$$

(c) Since $\textbf{v} = \textbf{w} + (\textbf{v} - \textbf{w})$, then $\norm{\textbf{v}} = \norm{\textbf{w} + (\textbf{v} - \textbf{w})} \le \norm{\textbf{w}} + \norm{\textbf{v} - \textbf{w}}$ by the Triangle Inequality, so subtracting $\norm{\textbf{w}}$ from both sides gives $\norm{\textbf{v}} - \norm{\textbf{w}} \le \norm{\textbf{v} - \textbf{w}}$.

The Triangle Inequality gets its name from the fact that in any triangle, no one side is longer than the sum of the lengths of the other two sides (see Figure 1.3.4). Another way of saying this is with the familiar statement "the shortest distance between two points is a straight line.''

Figure 1.3.4