3.1: Double Integrals
- Page ID
- 2242
In single-variable calculus, differentiation and integration are thought of as inverse operations. For instance, to integrate a function \(f (x)\) it is necessary to find the antiderivative of \(f\), that is, another function \(F(x)\) whose derivative is \(f (x)\). Is there a similar way of defining integration of real-valued functions of two or more variables? The answer is yes, as we will see shortly. Recall also that the definite integral of a nonnegative function \(f (x) \ge 0\) represented the area “under” the curve \(y = f (x)\). As we will now see, the double integral of a nonnegative real-valued function \(f (x, y) \ge 0\) represents the volume “under” the surface \(z = f (x, y)\).
Let \(f (x, y)\) be a continuous function such that \(f (x, y) \ge 0 \text{ for all }(x, y)\) on the rectangle \(R = {(x, y) : a ≤ x ≤ b, c ≤ y ≤ d}\) in \(\mathbb{R}^2\). We will often write this as \(R = [a,b] \times [c,d]\). For any number \(x∗\) in the interval \([a,b]\), slice the surface \(z = f (x, y)\) with the plane \(x = x∗\) parallel to the \(yz\)-plane. Then the trace of the surface in that plane is the curve \(f (x∗, y)\), where \(x∗\) is fixed and only \(y\) varies. The area \(A\) under that curve (i.e. the area of the region between the curve and the \(x y\)-plane) as \(y\) varies over the interval \([c,d]\) then depends only on the value of \(x∗\). So using the variable \(x\) instead of \(x∗\), let \(A(x)\) be that area (see Figure 3.1.1).
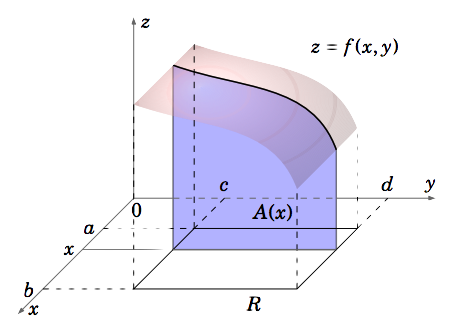
Then \(A(x) = \int_c^d f (x, y)d y\) since we are treating \(x\) as fixed, and only \(y\) varies. This makes sense since for a fixed \(x\) the function \(f (x, y)\) is a continuous function of \(y\) over the interval \([c,d]\), so we know that the area under the curve is the definite integral. The area \(A(x)\) is a function of \(x\), so by the “slice” or cross-section method from single-variable calculus we know that the volume \(V\) of the solid under the surface \(z = f (x, y)\) but above the \(x y\)-plane over the rectangle \(R\) is the integral over \([a,b]\) of that cross-sectional area \(A(x)\):
\[V = \int_a^b A(x)dx = \int_a^b \left [\int_c^d f (x, y)d y \right ] dx \label{Eq3.1}\]
We will always refer to this volume as “the volume under the surface”. The above expression uses what are called iterated integrals. First the function \(f (x, y)\) is integrated as a function of \(y\), treating the variable \(x\) as a constant (this is called integrating with respect to \(y\)). That is what occurs in the “inner” integral between the square brackets in Equation \ref{Eq3.1}. This is the first iterated integral. Once that integration is performed, the result is then an expression involving only \(x\), which can then be integrated with respect to \(x\). That is what occurs in the “outer” integral above (the second iterated integral). The final result is then a number (the volume). This process of going through two iterations of integrals is called double integration, and the last expression in Equation \ref{Eq3.1} is called a double integral.
Notice that integrating \(f (x, y)\) with respect to \(y\) is the inverse operation of taking the partial derivative of \(f (x, y)\) with respect to \(y\). Also, we could just as easily have taken the area of cross-sections under the surface which were parallel to the \(xz\)-plane, which would then depend only on the variable \(y\), so that the volume \(V\) would be
\[V = \int_c^d \left [\int_a^b f (x, y)dx \right ] dy \label{Eq3.2}\]
It turns out that in general the order of the iterated integrals does not matter. Also, we will usually discard the brackets and simply write
\[V=\int_c^d \int_a^b f (x, y)dx d y \label{Eq3.3}\]
where it is understood that the fact that \(dx\) is written before \(d y\) means that the function \(f (x, y)\) is first integrated with respect to \(x\) using the “inner” limits of integration \(a \text{ and }b\), and then the resulting function is integrated with respect to y using the “outer” limits of integration \(c \text{ and }d\). This order of integration can be changed if it is more convenient.
Example 3.1
Find the volume \(V\) under the plane \(z = 8x +6y\) over the rectangle \(R = [0,1]\times [0,2]\).
Solution
We see that \(f (x, y) = 8x+6y \ge 0 \text{ for }0 \le x \le 1 \text{ and }0 \le y \le 2\), so:
\[\nonumber \begin{align} V&=\int_0^2 \int_0^1 (8x+6y)dx \,d y \\[4pt] \nonumber &= \int_0^2 \left ( 4x^2 +6x y \big |_{x=0}^{x=1} \right )dy \\[4pt] \nonumber &=\int_0^2 (4+6y)d y \\[4pt] \nonumber &=4y+3y^2 \big |_0^2 \\[4pt] &=20 \end{align}\]
Suppose we had switched the order of integration. We can verify that we still get the same answer:
\[\nonumber \begin{align}V&=\int_0^1 \int_0^2 (8x+6y)dy \,d x \\[4pt] \nonumber &=\int_0^1 \left ( 8x y+3y^2 \big |_{y=0}^{y=2} \right )dx \\[4pt] \nonumber &=\int_0^1 (16x+12)dx \\[4pt] &=8x^2 +12x \big |_0^1 \\[4pt] \nonumber &=20 \end{align}\]
Example 3.2
Find the volume \(V\) under the surface \(z = e^{x+y}\) over the rectangle \(R = [2,3] \times [1,2]\).
Solution
We know that \(f (x, y) = e^{x+y} > 0 \text{ for all }(x, y)\), so
\[\nonumber \begin{align} V &=\int_1^2 \int_2^3 e^{x+y} dx\, d y \\[4pt] \nonumber &= \int_1^2 \left (e^{x+y} \big |_{x=2}^{x=3} \right )dy \\[4pt] \nonumber &= \int_1^2 (e^{y+3}-e^{y+2})dy \\[4pt] \nonumber &= e^{y+3}-e^{y+2} \big |_1^2 \\[4pt] \nonumber &= e^5 − e^4 −(e^4 − e^3 ) = e^5 −2e^4 + e^3 \end{align} \]
Recall that for a general function \(f (x)\), the integral \(\int_a^b f (x)dx\) represents the difference of the area below the curve \(y = f (x)\) but above the \(x\)-axis when \(f (x) \ge 0\), and the area above the curve but below the \(x\)-axis when \(f (x) \le 0\). Similarly, the double integral of any continuous function \(f (x, y)\) represents the difference of the volume below the surface \(z = f (x, y)\) but above the \(x y\)-plane when \(f (x, y) \ge 0\), and the volume above the surface but below the \(x y\)-plane when \(f (x, y) \le 0\). Thus, our method of double integration by means of iterated integrals can be used to evaluate the double integral of any continuous function over a rectangle, regardless of whether \(f (x, y) \ge 0\) or not.
Example 3.3
Evaluate \(\int_0^{2\pi}\int_0^{\pi}sin(x+y)dx\,dy \)
Solution
Note that \(f (x, y) = sin(x+ y)\) is both positive and negative over the rectangle \([0,\pi]\times [0,2\pi]\). We can still evaluate the double integral:
\[\nonumber \begin{align} \int_0^{2\pi} \int_0^{\pi}sin(x+y)dx\,dy &=\int_0^{2\pi} \left (-cos(x+y)\big |_{x=0}^{x=\pi} \right )dy \\[4pt] \nonumber &= \int_0^{2\pi} (-cos(y+\pi)+cos{\,y})dy \\[4pt] \nonumber &=-sin(y+\pi)+sin{\,y}\big |_0^{2\pi} = -sin{\,3\pi}+sin{\,2\pi} - (-sin{\,\pi}+sin{\,0}) \\[4pt] \nonumber &=0 \end{align} \]


