4.7: Exponential and Logarithmic Models
- Last updated
- Save as PDF
- Page ID
- 1358
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Model exponential growth and decay.
- Use Newton’s Law of Cooling.
- Use logistic-growth models.
- Choose an appropriate model for data.
- Express an exponential model in base \(e\).
We have already explored some basic applications of exponential and logarithmic functions. In this section, we explore some important applications in more depth, including radioactive isotopes and Newton’s Law of Cooling.

Modeling Exponential Growth and Decay
In real-world applications, we need to model the behavior of a function. In mathematical modeling, we choose a familiar general function with properties that suggest that it will model the real-world phenomenon we wish to analyze. In the case of rapid growth, we may choose the exponential growth function:
\[y=A_0e^{kt}\]
where \(A_0\) is equal to the value at time zero, \(e\) is Euler’s constant, and \(k\) is a positive constant that determines the rate (percentage) of growth. We may use the exponential growth function in applications involving doubling time, the time it takes for a quantity to double. Such phenomena as wildlife populations, financial investments, biological samples, and natural resources may exhibit growth based on a doubling time. In some applications, however, as we will see when we discuss the logistic equation, the logistic model sometimes fits the data better than the exponential model.
On the other hand, if a quantity is falling rapidly toward zero, without ever reaching zero, then we should probably choose the exponential decay model. Again, we have the form \(y=A_0e^{kt}\) where \(A_0\) is the starting value, and \(e\) is Euler’s constant. Now \(k\) is a negative constant that determines the rate of decay. We may use the exponential decay model when we are calculating half-life, or the time it takes for a substance to exponentially decay to half of its original quantity. We use half-life in applications involving radioactive isotopes.
In our choice of a function to serve as a mathematical model, we often use data points gathered by careful observation and measurement to construct points on a graph and hope we can recognize the shape of the graph. Exponential growth and decay graphs have a distinctive shape, as we can see in Figure \(\PageIndex{2}\) and Figure \(\PageIndex{3}\). It is important to remember that, although parts of each of the two graphs seem to lie on the \(x\)-axis, they are really a tiny distance above the \(x\)-axis.
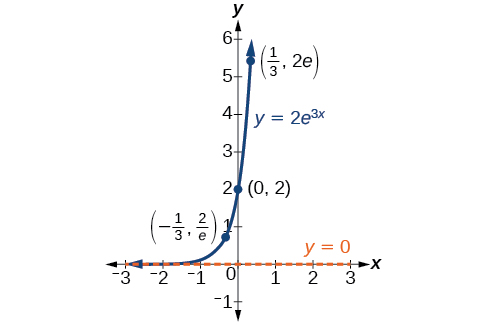
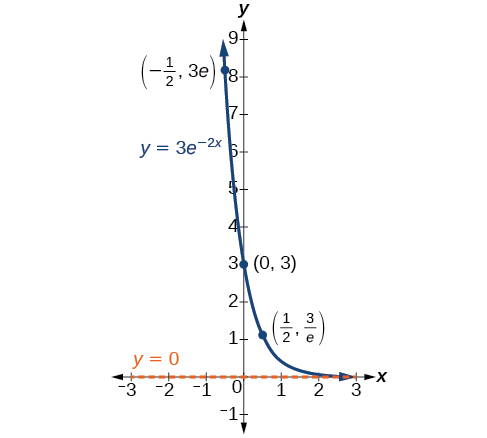
Exponential growth and decay often involve very large or very small numbers. To describe these numbers, we often use orders of magnitude. The order of magnitude is the power of ten, when the number is expressed in scientific notation, with one digit to the left of the decimal. For example, the distance to the nearest star, Proxima Centauri, measured in kilometers, is \(40,113,497,200,000\) kilometers. Expressed in scientific notation, this is \(4.01134972 × 1013\). So, we could describe this number as having order of magnitude \(1013\).
\(y=a_0e^{kt}\)
An exponential function with the form \(y=A_0e^{kt}\) has the following characteristics:
- one-to-one function
- horizontal asymptote: \(y=0\)
- domain: \((–\infty, \infty)\)
- range: \((0,\infty)\)
- \(x\) intercept: none
- \(y\)-intercept: \((0,A_0)\)
- increasing if \(k>0\) (see Figure \(\PageIndex{4}\))
- decreasing if \(k<0\) (see Figure \(\PageIndex{4}\))
Example \(\PageIndex{1}\): Graphing Exponential Growth
A population of bacteria doubles every hour. If the culture started with \(10\) bacteria, graph the population as a function of time.
Solution
When an amount grows at a fixed percent per unit time, the growth is exponential. To find \(A_0\) we use the fact that \(A_0\) is the amount at time zero, so \(A_0=10\). To find \(k\), use the fact that after one hour \((t=1)\) the population doubles from \(10\) to \(20\).The formula is derived as follows
\[\begin{align*} 20&= 10e^{k\cdot 1}\\ 2&= e^k \qquad \text{Divide by 10}\\ \ln2&= k \qquad \text{Take the natural logarithm} \end{align*}\]
so \(k=\ln(2)\). Thus the equation we want to graph is \(y=10e^{(\ln2)t}=10{(e^{\ln2})}^t=10·2^t\). The graph is shown in Figure \(\PageIndex{5}\).
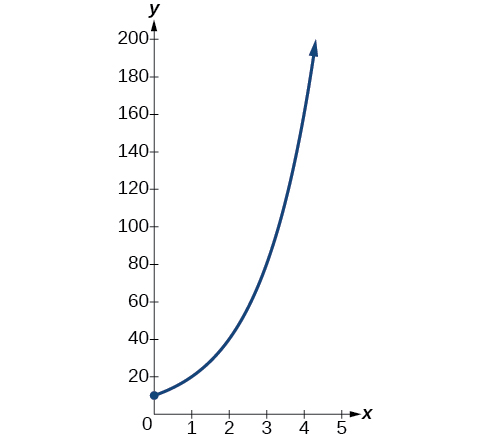
Analysis
The population of bacteria after ten hours is \(10,240\). We could describe this amount is being of the order of magnitude \(10^4\). The population of bacteria after twenty hours is \(10,485,760\) which is of the order of magnitude \(10^7\), so we could say that the population has increased by three orders of magnitude in ten hours.
Half-Life
We now turn to exponential decay. One of the common terms associated with exponential decay, as stated above, is half-life, the length of time it takes an exponentially decaying quantity to decrease to half its original amount. Every radioactive isotope has a half-life, and the process describing the exponential decay of an isotope is called radioactive decay.
To find the half-life of a function describing exponential decay, solve the following equation:
\(\dfrac{1}{2}A_0=A_0e^{kt}\)
We find that the half-life depends only on the constant \(k\) and not on the starting quantity \(A_0\).
The formula is derived as follows
\[\begin{align*} \dfrac{1}{2}A_0&= A_0e^{kt}\\ \dfrac{1}{2}&= e^{kt} \qquad \text{Divide by } A_0\\ \ln \left (\dfrac{1}{2} \right )&= ktv \qquad \text{Take the natural log}\\ -\ln(2)&= kt \qquad \text{Apply laws of logarithms}\\ -\ln(2)k&= t \qquad \text{Divide by k} \end{align*}\]
Since \(t\), the time, is positive, \(k\) must, as expected, be negative. This gives us the half-life formula
\[t=−\dfrac{\ln(2)}{k}\]
Given the half-life, find the decay rate.
- Write \(A=A_0e^{kt}\).
- Replace \(A\) by \(\dfrac{1}{2}A_0\) and replace \(t\) by the given half-life.
- Solve to find \(k\). Express \(k\) as an exact value (do not round).
Note: It is also possible to find the decay rate using \(k=−\ln(2)t\).
Example \(\PageIndex{2}\): Finding the Function that Describes Radioactive Decay
The half-life of carbon-14 is \(5,730\) years. Express the amount of carbon-14 remaining as a function of time, \(t\).
Solution
This formula is derived as follows.
\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for } f(t)\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{ \left (\tfrac{\ln(0.5)}{5730} \right ) t} \qquad \text{Substitute for r in the continuous growth formula} \end{align*}\]
The function that describes this continuous decay is \(f(t)=A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\). We observe that the coefficient of \(t\), \(\dfrac{\ln(0.5)}{5730}≈−1.2097×10^{−4}\) is negative, as expected in the case of exponential decay.
Exercise \(\PageIndex{1}\)
The half-life of plutonium-244 is \(80,000,000\) years. Find function gives the amount of carbon-14 remaining as a function of time, measured in years.
- Answer
-
\(f(t)=A_0e^{−0.0000000087t}\)
Radiocarbon Dating
The formula for radioactive decay is important in radiocarbon dating, which is used to calculate the approximate date a plant or animal died. Radiocarbon dating was discovered in 1949 by Willard Libby, who won a Nobel Prize for his discovery. It compares the difference between the ratio of two isotopes of carbon in an organic artifact or fossil to the ratio of those two isotopes in the air. It is believed to be accurate to within about \(1\%\) error for plants or animals that died within the last \(60,000\) years.
Carbon-14 is a radioactive isotope of carbon that has a half-life of \(5,730\) years. It occurs in small quantities in the carbon dioxide in the air we breathe. Most of the carbon on Earth is carbon-12, which has an atomic weight of \(12\) and is not radioactive. Scientists have determined the ratio of carbon-14 to carbon-12 in the air for the last \(60,000\) years, using tree rings and other organic samples of known dates—although the ratio has changed slightly over the centuries.
As long as a plant or animal is alive, the ratio of the two isotopes of carbon in its body is close to the ratio in the atmosphere. When it dies, the carbon-14 in its body decays and is not replaced. By comparing the ratio of carbon-14 to carbon-12 in a decaying sample to the known ratio in the atmosphere, the date the plant or animal died can be approximated.
Since the half-life of carbon-14 is \(5,730\) years, the formula for the amount of carbon-14 remaining after \(t\) years is
\(A≈A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\)
where
- \(A\) is the amount of carbon-14 remaining
- \(A_0\) is the amount of carbon-14 when the plant or animal began decaying.
This formula is derived as follows:
\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for f(t)}\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t} \qquad \text{Substitute for r in the continuous growth formula}\\ \end{align*}\]
To find the age of an object, we solve this equation for \(t\):
\(t=\dfrac{\ln \left (\dfrac{A}{A_0} \right )}{−0.000121}\)
Out of necessity, we neglect here the many details that a scientist takes into consideration when doing carbon-14 dating, and we only look at the basic formula. The ratio of carbon-14 to carbon-12 in the atmosphere is approximately \(0.0000000001%\). Let \(r\) be the ratio of carbon-14 to carbon-12 in the organic artifact or fossil to be dated, determined by a method called liquid scintillation. From the equation \(A≈A_0e^{−0.000121t}\) we know the ratio of the percentage of carbon-14 in the object we are dating to the percentage of carbon-14 in the atmosphere is \(r=\dfrac{A}{A_0}≈e^{−0.000121t}\). We solve this equation for \(t\), to get
\(t=\dfrac{\ln(r)}{−0.000121}\)
- Express the given percentage of carbon-14 as an equivalent decimal, \(k\).
- Substitute for \(k\) in the equation \(t=\dfrac{\ln(r)}{−0.000121}\) and solve for the age, \(t\).
Example \(\PageIndex{3}\): Finding the Age of a Bone
A bone fragment is found that contains \(20\%\) of its original carbon-14. To the nearest year, how old is the bone?
Solution
We substitute \(20\%=0.20\) for \(k\) in the equation and solve for \(t\):
\[\begin{align*} t&= \dfrac{\ln(r)}{-0.000121} \qquad \text{Use the general form of the equation}\\ &= \dfrac{\ln(0.20)}{-0.000121} \qquad \text{Substitute for r}\\ &\approx 13301 \qquad \text{Round to the nearest year} \end{align*}\]
The bone fragment is about \(13,301\) years old.
Analysis
The instruments that measure the percentage of carbon-14 are extremely sensitive and, as we mention above, a scientist will need to do much more work than we did in order to be satisfied. Even so, carbon dating is only accurate to about \(1\%\), so this age should be given as \(13,301\) years \(\pm 1\%\) or \(13,301\) years \(\pm 133\) years.
Exercise \(\PageIndex{2}\)
Cesium-137 has a half-life of about \(30\) years. If we begin with \(200\) mg of cesium-137, will it take more or less than \(230\) years until only \(1\) milligram remains?
- Answer
-
less than \(230\) years, \(229.3157\) to be exact
Calculating Doubling Time
For decaying quantities, we determined how long it took for half of a substance to decay. For growing quantities, we might want to find out how long it takes for a quantity to double. As we mentioned above, the time it takes for a quantity to double is called the doubling time.
Given the basic exponential growth equation \(A=A_0e^{kt}\), doubling time can be found by solving for when the original quantity has doubled, that is, by solving \(2A_0=A_0e^{kt}\).
The formula is derived as follows:
\[\begin{align*} 2A_0&= A_0e^{kt}\\ 2&= e^{kt} \qquad \text{Divide by } A_0\\ \ln2&= kt \qquad \text{Take the natural logarithm}\\ t& =\dfrac{\ln2}{k} \qquad \text{Divide by the coefficient of t} \end{align*}\]
Thus the doubling time is
\[t=\dfrac{\ln2}{k}\]
Example \(\PageIndex{4}\): Finding a Function That Describes Exponential Growth
According to Moore’s Law, the doubling time for the number of transistors that can be put on a computer chip is approximately two years. Give a function that describes this behavior.
Solution
The formula is derived as follows:
\[\begin{align*} t&= \dfrac{\ln2}{k} \qquad \text{The doubling time formula}\\ 2&= \dfrac{\ln2}{k} \qquad \text{Use a doubling time of two years}\\ k&= \dfrac{\ln2}{2} \qquad \text{Multiply by k and divide by 2}\\ A&= A_0e^{\tfrac{\ln2}{2}t} \qquad \text{Substitute k into the continuous growth formula} \end{align*}\]
The function is \(A=A_0e^{\dfrac{\ln2}{2}t}\).
Exercise \(\PageIndex{3}\)
Recent data suggests that, as of 2013, the rate of growth predicted by Moore’s Law no longer holds. Growth has slowed to a doubling time of approximately three years. Find the new function that takes that longer doubling time into account.
- Answer
-
\(f(t)=A_0e^{\tfrac{\ln2}{3}t}\)
Using Newton’s Law of Cooling
Exponential decay can also be applied to temperature. When a hot object is left in surrounding air that is at a lower temperature, the object’s temperature will decrease exponentially, leveling off as it approaches the surrounding air temperature. On a graph of the temperature function, the leveling off will correspond to a horizontal asymptote at the temperature of the surrounding air. Unless the room temperature is zero, this will correspond to a vertical shift of the generic exponential decay function. This translation leads to Newton’s Law of Cooling, the scientific formula for temperature as a function of time as an object’s temperature is equalized with the ambient temperature
\(T(t)=ae^{kt}+T_s\)
This formula is derived as follows:
\[\begin{align*} T(t)&= Ab^{ct}+T_s\\ T(t)&= Ae^{\ln(b^{ct})}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{ct\ln b}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{kt}+T_s \qquad \text{Rename the constant c } ln b \text{, calling it } k\\ \end{align*}\]
NEWTON’S LAW OF COOLING
The temperature of an object, \(T\), in surrounding air with temperature \(T_s\) will behave according to the formula
\[T(t)=Ae^{kt}+T_s\]
where- \(t\) is time
- \(A\) is the difference between the initial temperature of the object and the surroundings
- \(k\) is a constant, the continuous rate of cooling of the object
Given a set of conditions, apply Newton’s Law of Cooling.
- Set \(T_s\) equal to the \(y\)-coordinate of the horizontal asymptote (usually the ambient temperature).
- Substitute the given values into the continuous growth formula \(T(t)=Ae^{kt}+T_s\) to find the parameters \(A\) and \(k\).
- Substitute in the desired time to find the temperature or the desired temperature to find the time.
Example \(\PageIndex{5}\): Using Newton’s Law of Cooling
A cheesecake is taken out of the oven with an ideal internal temperature of \(165°F\), and is placed into a \(35°F\) refrigerator. After \(10\) minutes, the cheesecake has cooled to \(150°F\). If we must wait until the cheesecake has cooled to \(70°F\) before we eat it, how long will we have to wait?
Solution
Because the surrounding air temperature in the refrigerator is \(35\) degrees, the cheesecake’s temperature will decay exponentially toward \(35\), following the equation
\(T(t)=Ae^{kt}+35\)
We know the initial temperature was \(165\), so \(T(0)=165\).
\[\begin{align*} 165&= Ae^{k0}+35 \qquad \text{Substitute } (0,165)\\ A&= 130 \qquad \text{Solve for A} \end{align*}\]
We were given another data point, \(T(10)=150\), which we can use to solve for \(k\).
\[\begin{align*} 150&= 130e^{k10}+35 \qquad \text{Substitute } (10, 150)\\ 115&= 130e^{k10} \qquad \text{Subtract 35}\\ \dfrac{115}{130}&= e^{10k} \qquad \text{Divide by 130}\\ \ln\left (\dfrac{115}{130} \right )&= 10k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln \left (\dfrac{115}{130} \right )}{10}\\ &= -0.0123 \qquad \text{Divide by the coefficient of k} \end{align*}\]
This gives us the equation for the cooling of the cheesecake: \(T(t)=130e^{–0.0123t}+35\).
Now we can solve for the time it will take for the temperature to cool to \(70\) degrees.
\[\begin{align*} 70&= 130e^{-0.0123t}+35 \qquad \text{Substitute in 70 for } T(t)\\ 35&= 130e^{-0.0123t} \qquad \text{Subtract 35}\\ \dfrac{35}{130}&= e^{-0.0123t} \qquad \text{Divide by 130}\\ \ln \left (\dfrac{35}{130} \right )&= -0.0123t \qquad \text{Take the natural log of both sides}\\ t&= \dfrac{\ln \left (\dfrac{35}{130} \right )}{-0.0123}\\ &\approx 106.68 \qquad \text{Divide by the coefficient of t} \end{align*}\]
It will take about \(107\) minutes, or one hour and \(47\) minutes, for the cheesecake to cool to \(70°F\).
Exercise \(\PageIndex{4}\)
A pitcher of water at \(40\) degrees Fahrenheit is placed into a \(70\) degree room. One hour later, the temperature has risen to \(45\) degrees. How long will it take for the temperature to rise to \(60\) degrees?
- Answer
-
\(6.026\) hours
Using Logistic Growth Models
Exponential growth cannot continue forever. Exponential models, while they may be useful in the short term, tend to fall apart the longer they continue. Consider an aspiring writer who writes a single line on day one and plans to double the number of lines she writes each day for a month. By the end of the month, she must write over \(17\) billion lines, or one-half-billion pages. It is impractical, if not impossible, for anyone to write that much in such a short period of time. Eventually, an exponential model must begin to approach some limiting value, and then the growth is forced to slow. For this reason, it is often better to use a model with an upper bound instead of an exponential growth model, though the exponential growth model is still useful over a short term, before approaching the limiting value.
The logistic growth model is approximately exponential at first, but it has a reduced rate of growth as the output approaches the model’s upper bound, called the carrying capacity. For constants \(a\), \(b\), and \(c\), the logistic growth of a population over time \(x\) is represented by the model
\(f(x)=\dfrac{c}{1+ae^{−bx}}\)
The graph in Figure \(\PageIndex{6}\) shows how the growth rate changes over time. The graph increases from left to right, but the growth rate only increases until it reaches its point of maximum growth rate, at which point the rate of increase decreases.
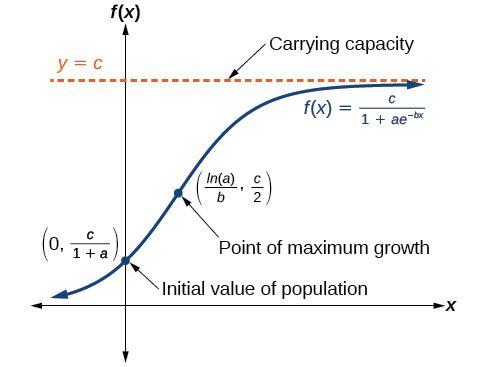
LOGISTIC GROWTH
The logistic growth model is
\[f(x)=\dfrac{c}{1+ae^{−bx}}\]
where
- \(\dfrac{c}{1+a}\) is the initial value
- \(c\) is the carrying capacity, or limiting value
- \(b\) is a constant determined by the rate of growth.
Example \(\PageIndex{6}\): Using the Logistic-Growth Model
An influenza epidemic spreads through a population rapidly, at a rate that depends on two factors: The more people who have the flu, the more rapidly it spreads, and also the more uninfected people there are, the more rapidly it spreads. These two factors make the logistic model a good one to study the spread of communicable diseases. And, clearly, there is a maximum value for the number of people infected: the entire population.
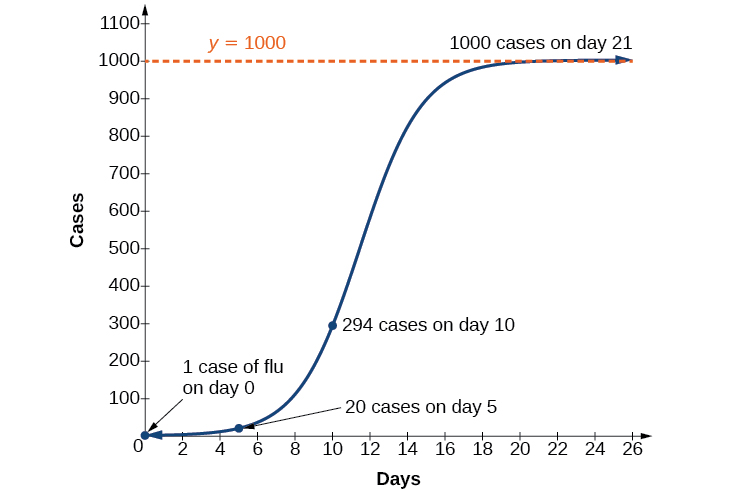
For example, at time \(t=0\) there is one person in a community of \(1,000\) people who has the flu. So, in that community, at most \(1,000\) people can have the flu. Researchers find that for this particular strain of the flu, the logistic growth constant is \(b=0.6030\). Estimate the number of people in this community who will have had this flu after ten days. Predict how many people in this community will have had this flu after a long period of time has passed.
Solution
We substitute the given data into the logistic growth model
\(f(x)=\dfrac{c}{1+ae^{−bx}}\)
Because at most \(1,000\) people, the entire population of the community, can get the flu, we know the limiting value is \(c=1000\). To find \(a\),we use the formula that the number of cases at time \(t=0\) is \(\dfrac{c}{1+a}=1\), from which it follows that \(a=999\).This model predicts that, after ten days, the number of people who have had the flu is \(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}≈293.8\). Because the actual number must be a whole number (a person has either had the flu or not) we round to \(294\). In the long term, the number of people who will contract the flu is the limiting value, \(c=1000\).
Analysis
Remember that, because we are dealing with a virus, we cannot predict with certainty the number of people infected. The model only approximates the number of people infected and will not give us exact or actual values.
The graph in Figure \(\PageIndex{7}\) gives a good picture of how this model fits the data.
Exercise \(\PageIndex{5}\)
Using the model in the Example above, estimate the number of cases of flu on day \(15\).
- Answer
-
\(895\) cases on day \(15\)
Choosing an Appropriate Model for Data
Now that we have discussed various mathematical models, we need to learn how to choose the appropriate model for the raw data we have. Many factors influence the choice of a mathematical model, among which are experience, scientific laws, and patterns in the data itself. Not all data can be described by elementary functions. Sometimes, a function is chosen that approximates the data over a given interval. For instance, suppose data were gathered on the number of homes bought in the United States from the years 1960 to 2013. After plotting these data in a scatter plot, we notice that the shape of the data from the years 2000 to 2013 follow a logarithmic curve. We could restrict the interval from 2000 to 2010, apply regression analysis using a logarithmic model, and use it to predict the number of home buyers for the year 2015.
Three kinds of functions that are often useful in mathematical models are linear functions, exponential functions, and logarithmic functions. If the data lies on a straight line, or seems to lie approximately along a straight line, a linear model may be best. If the data is non-linear, we often consider an exponential or logarithmic model, though other models, such as quadratic models, may also be considered.
In choosing between an exponential model and a logarithmic model, we look at the way the data curves. This is called the concavity. If we draw a line between two data points, and all (or most) of the data between those two points lies above that line, we say the curve is concave down. We can think of it as a bowl that bends downward and therefore cannot hold water. If all (or most) of the data between those two points lies below the line, we say the curve is concave up. In this case, we can think of a bowl that bends upward and can therefore hold water. An exponential curve, whether rising or falling, whether representing growth or decay, is always concave up away from its horizontal asymptote. A logarithmic curve is always concave away from its vertical asymptote. In the case of positive data, which is the most common case, an exponential curve is always concave up, and a logarithmic curve always concave down.
A logistic curve changes concavity. It starts out concave up and then changes to concave down beyond a certain point, called a point of inflection.
After using the graph to help us choose a type of function to use as a model, we substitute points, and solve to find the parameters. We reduce round-off error by choosing points as far apart as possible.
Example \(\PageIndex{7}\): Choosing a Mathematical Model
Does a linear, exponential, logarithmic, or logistic model best fit the values listed in Table \(\PageIndex{1}\)? Find the model, and use a graph to check your choice.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 0 | 1.386 | 2.197 | 2.773 | 3.219 | 3.584 | 3.892 | 4.159 | 4.394 |
Solution
First, plot the data on a graph as in Figure \(\PageIndex{8}\). For the purpose of graphing, round the data to two significant digits.
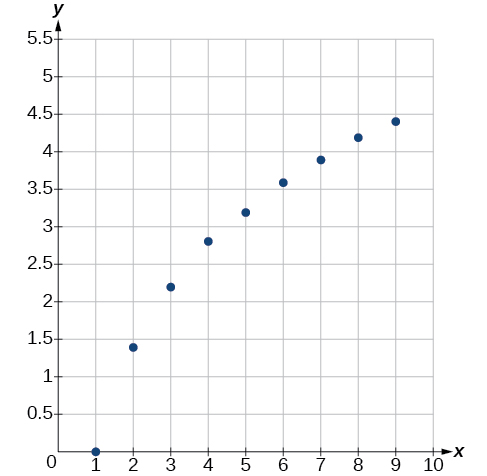
Clearly, the points do not lie on a straight line, so we reject a linear model. If we draw a line between any two of the points, most or all of the points between those two points lie above the line, so the graph is concave down, suggesting a logarithmic model. We can try \(y=a\ln(bx)\). Plugging in the first point, \((1,0)\), gives \(0=a\ln b\). We reject the case that \(a=0\) (if it were, all outputs would be \(0\)), so we know \(\ln(b)=0\). Thus \(b=1\) and \(y=a\ln(x)\). Next we can use the point \((9,4.394)\) to solve for \(a\):
\[\begin{align*} y&= a\ln(x)\\ 4.394&= a\ln(9)\\ a&= \dfrac{4.394}{\ln(9)} \end{align*}\]
Because \(a=\dfrac{4.394}{\ln(9)}≈2\),an appropriate model for the data is \(y=2\ln(x)\).
To check the accuracy of the model, we graph the function together with the given points as in Figure \(\PageIndex{9}\).
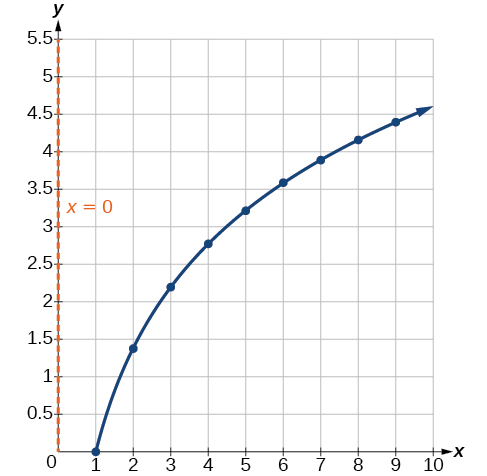
We can conclude that the model is a good fit to the data.
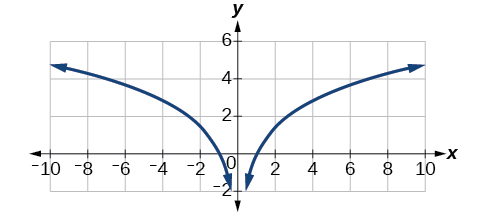
Compare Figure \(\PageIndex{9}\) to the graph of \(y=\ln(x^2)\) shown in Figure \(\PageIndex{10}\).
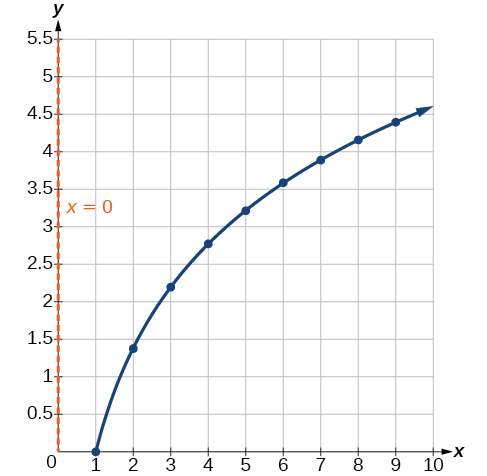
The graphs appear to be identical when \(x>0\). A quick check confirms this conclusion: \(y=\ln(x^2)=2\ln(x)\) for \(x>0\).
However, if \(x<0\), the graph of \(y=\ln(x^2)\) includes a “extra” branch, as shown in Figure \(\PageIndex{11}\). This occurs because, while \(y=2\ln(x)\) cannot have negative values in the domain (as such values would force the argument to be negative), the function \(y=\ln(x^2)\) can have negative domain values.
Exercise \(\PageIndex{6}\)
Does a linear, exponential, or logarithmic model best fit the data in Table \(\PageIndex{2}\)? Find the model.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 3.297 | 5.437 | 8.963 | 14.778 | 24.365 | 40.172 | 66.231 | 109.196 | 180.034 |
- Answer
-
Exponential \(y=2e^{0.5x}\).
Expressing an Exponential Model in Base \(e\)
While powers and logarithms of any base can be used in modeling, the two most common bases are \(10\) and \(e\). In science and mathematics, the base \(e\) is often preferred. We can use laws of exponents and laws of logarithms to change any base to base \(e\).
Given a model with the form \(y=ab^x\), change it to the form \(y=A_0e^{kx}\).
- Rewrite \(y=ab^x\) as \(y=ae^{\ln(b^x)}\).
- Use the power rule of logarithms to rewrite \(y\) as \(y=ae^{x\ln(b)}=ae^{\ln{(b)}^x}\).
- Note that \(a=A_0\) and \(k=\ln(b)\) in the equation \(y=A_0e^{kx}\).
Example \(\PageIndex{8}\): Changing to base \(e\)
Change the function \(y=2.5{(3.1)}^x\) so that this same function is written in the form \(y=A_0e^{kx}\).
Solution
The formula is derived as follows
\[\begin{align*} y&= 2.5{(3.1)}^x\\ &= 2.5e^{\ln({3.1}^x)} \qquad \text{Insert exponential and its inverse}\\ &= 2.5e^{x\ln3.1} \qquad \text{Laws of logs}\\ &= 2.5e^{(\ln3.1)x} \qquad \text{Commutative law of multiplication} \end{align*}\]
Exercise \(\PageIndex{7}\)
Change the function \(y=3{(0.5)}^x\) to one having \(e\) as the base.
- Answer
-
\(y=3e^{(\ln0.5)x}\)
Media
Access these online resources for additional instruction and practice with exponential and logarithmic models.
- Logarithm Application – pH
- Exponential Model – Age Using Half-Life
- Newton’s Law of Cooling
- Exponential Growth Given Doubling Time
- Exponential Growth – Find Initial Amount Given Doubling Time
Key Equations
| Half-life formula | If \(A=A_0e^{kt}\), \(k<0\), the half-life is \(t=−\dfrac{\ln(2)}{k}\). |
| Carbon-14 dating | \(t=\dfrac{\ln(\dfrac{A}{A_0})}{−0.000121}\). \(A_0\) \(A\) is the amount of carbon-14 when the plant or animal died \(t\) is the amount of carbon-14 remaining today is the age of the fossil in years |
| Doubling time formula | If \(A=A_0e^{kt}\), \(k>0\), the doubling time is \(t=\dfrac{\ln2}{k}\) |
| Newton’s Law of Cooling | \(T(t)=Ae^{kt}+T_s\), where \(T_s\) is the ambient temperature, \(A=T(0)−T_s\), and \(k\) is the continuous rate of cooling. |
Key Concepts
- The basic exponential function is \(f(x)=ab^x\). If \(b>1\),we have exponential growth; if \(0<b<1\), we have exponential decay.
- We can also write this formula in terms of continuous growth as \(A=A_0e^{kx}\), where \(A_0\) is the starting value. If \(A_0\) is positive, then we have exponential growth when \(k>0\) and exponential decay when \(k<0\). See Example \(\PageIndex{1}\).
- In general, we solve problems involving exponential growth or decay in two steps. First, we set up a model and use the model to find the parameters. Then we use the formula with these parameters to predict growth and decay. See Example \(\PageIndex{2}\).
- We can find the age, \(t\), of an organic artifact by measuring the amount, \(k\), of carbon-14 remaining in the artifact and using the formula \(t=\dfrac{\ln(k)}{−0.000121}\) to solve for \(t\). See Example \(\PageIndex{3}\).
- Given a substance’s doubling time or half-time, we can find a function that represents its exponential growth or decay. See Example \(\PageIndex{4}\).
- We can use Newton’s Law of Cooling to find how long it will take for a cooling object to reach a desired temperature, or to find what temperature an object will be after a given time. See Example \(\PageIndex{5}\).
- We can use logistic growth functions to model real-world situations where the rate of growth changes over time, such as population growth, spread of disease, and spread of rumors. See Example \(\PageIndex{6}\).
- We can use real-world data gathered over time to observe trends. Knowledge of linear, exponential, logarithmic, and logistic graphs help us to develop models that best fit our data. See Example \(\PageIndex{7}\).
- Any exponential function with the form \(y=abx\) can be rewritten as an equivalent exponential function with the form \(y=A_0e^{kx}\) where \(k=\ln b\). See Example \(\PageIndex{8}\).


